웅덩이

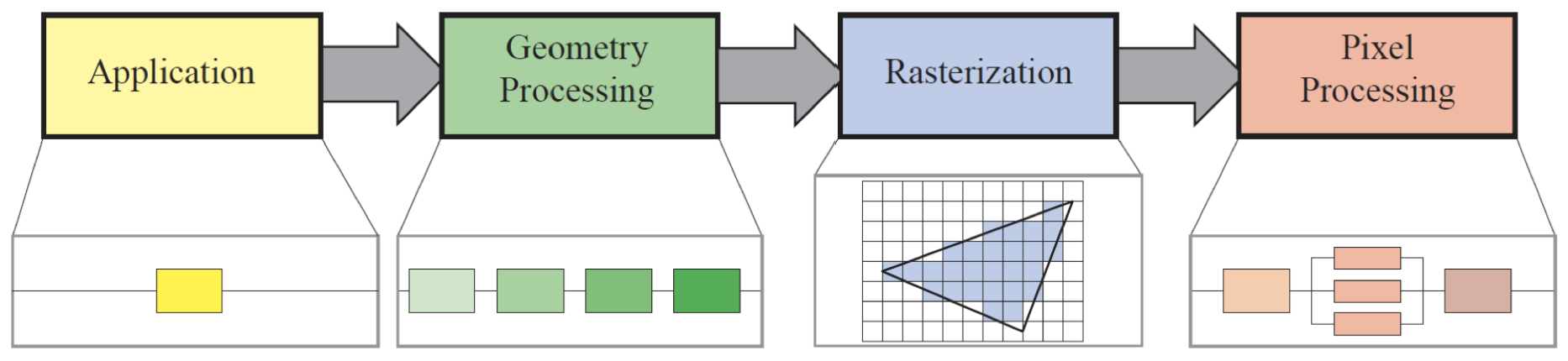
231210-002735

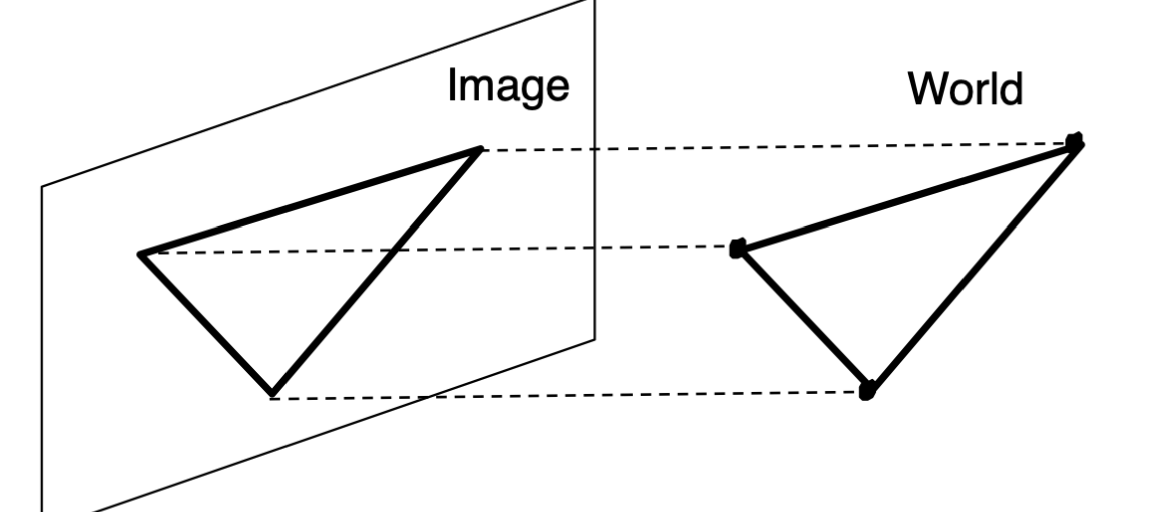
랜더링은 3D 세상의 정보를 2D의 영상으로 변환하는 과정을 의미합니다.
그 변환 과정을 세밀하게 알아봅시다.

Geometry processing

공간상의 좌표를 모니터의 좌표로 변환하기 위해서 좌표를 변환하는 과정이 필요한데, 그 순서와 변환법을 알아보겠습니다.

Viewing-transform

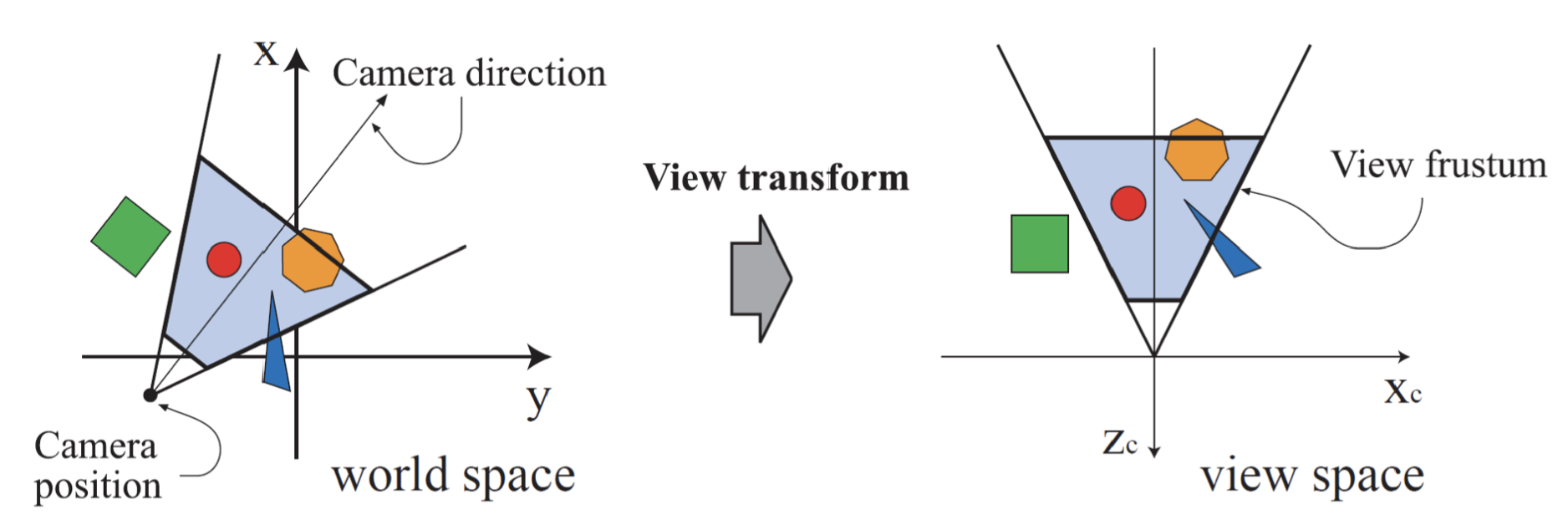
231209-233923

공간상의 좌표를 View plane 상에서 바라보는 곳의 좌표로 우선 변환합니다.

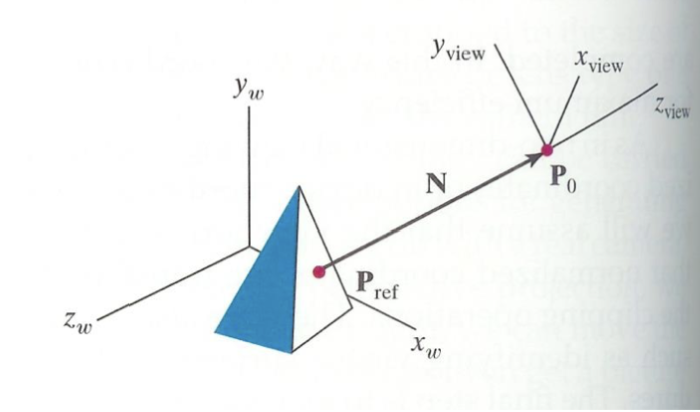
231209-234611

여기서 P는 카메라의 위치, N은 바라본 위치상의 평면(View plane)의 normal vector 입니다.
이 때, 사각 뿔 도형의 $P_{ref}$ 지점을 바라본다고 한다면, 법선 벡터 N은 $P_0 - P_{ref}$ 로 구할 수 있습니다.

여기서 View plane의 법선 벡터를 구했다고 View plane을 확정할 수는 없습니다.
왜냐하면 N을 축으로 회전이 가능하기 때문이죠.
따라서 View-up vector V를 정의합니다.

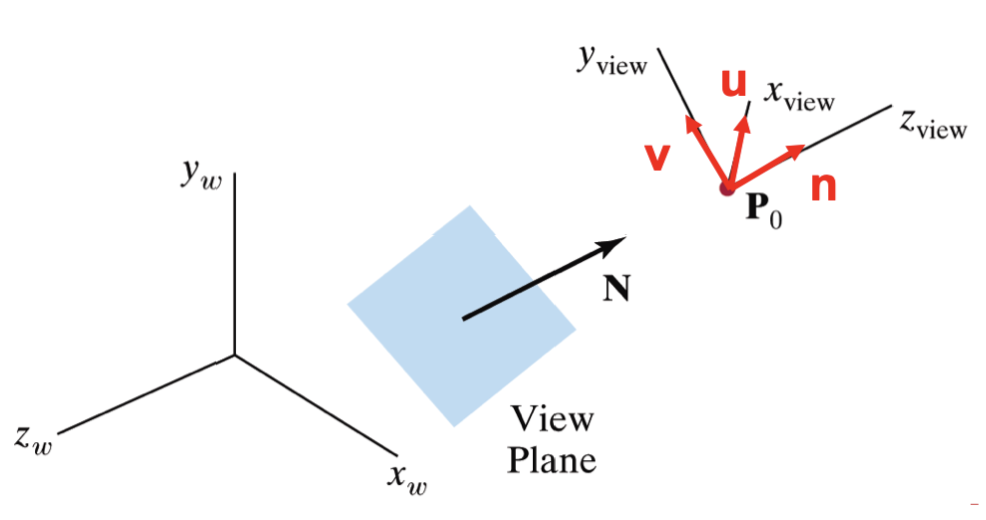
231209-234059

위에서 N, V를 구했다면, view space의 세 축을 정의할 수 있습니다.

n = \frac{N}{||N||} \\ {}\\ u = \frac{V \times n}{||V||} \\ {}\\ v = n \times u

이제 view space의 축의 벡터를 구했으니, world space의 물체를 view space로 좌표 변환이 가능합니다.
2차원을 예시로 들어보겠습니다.

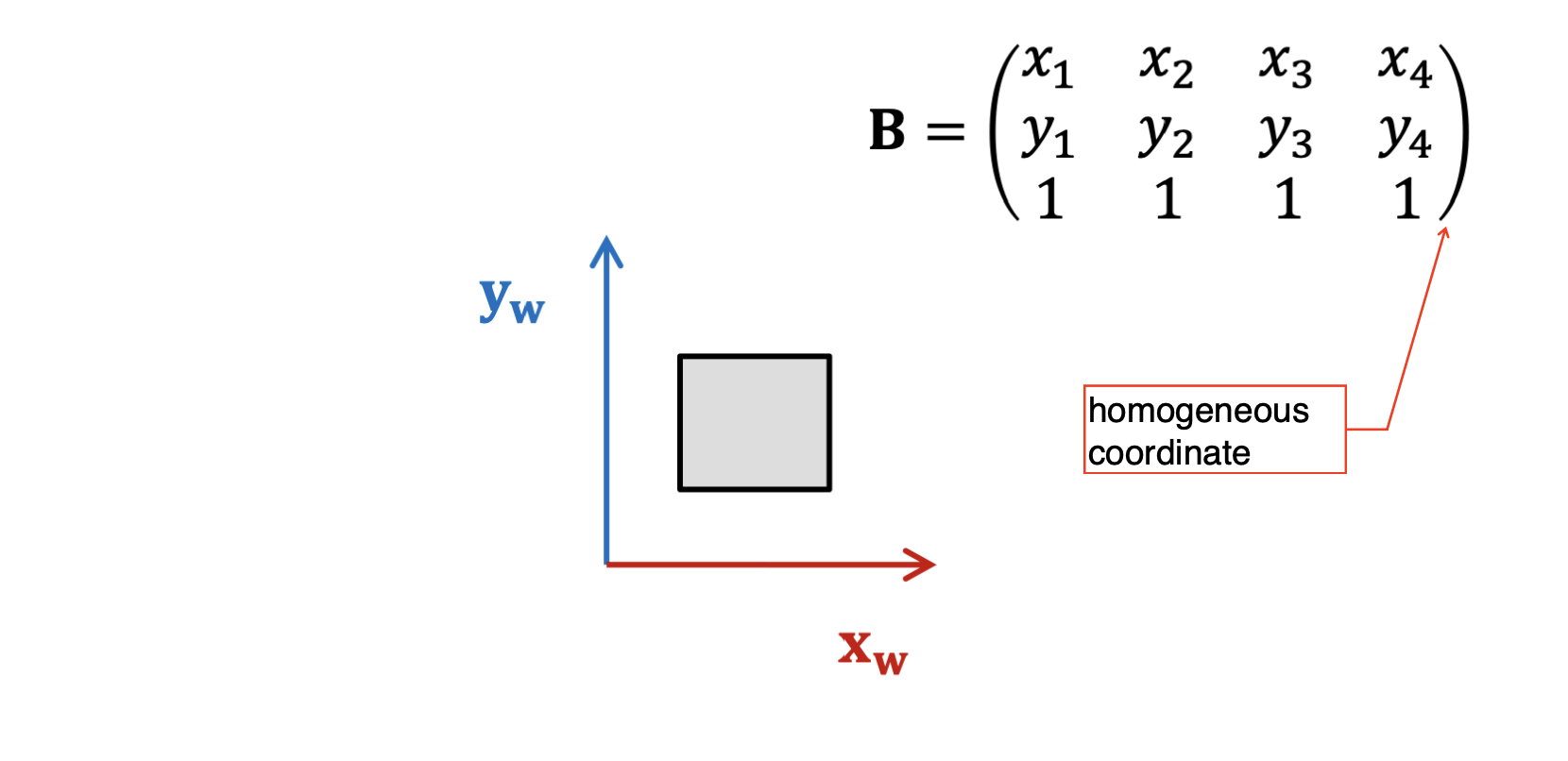
231209-235335

2차원의 물제의 좌표를 우선 homogeneous coordinate로 표현합니다.

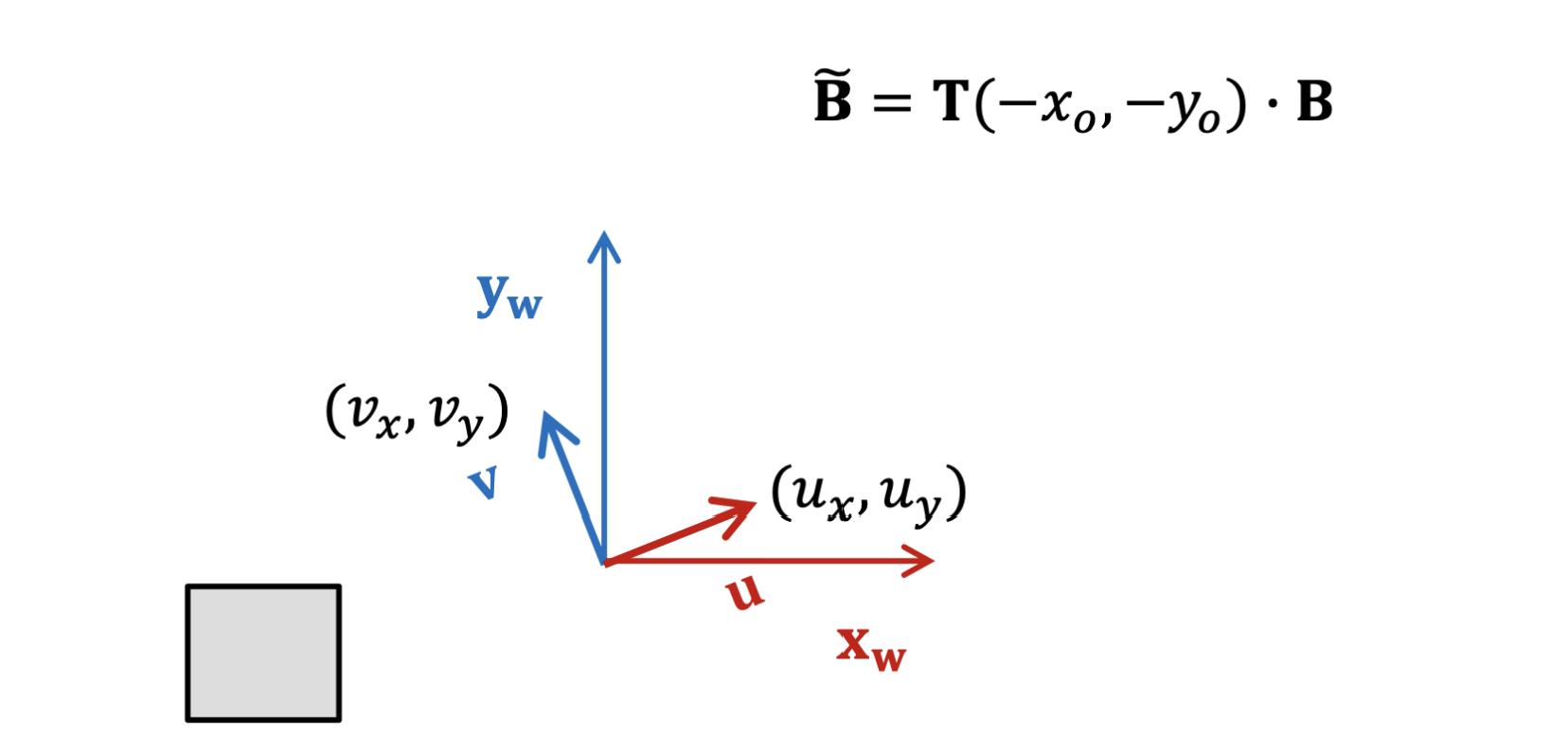
231209-235404

그리고 view coordinate를 word coordinate의 원점으로 이동시킵니다.

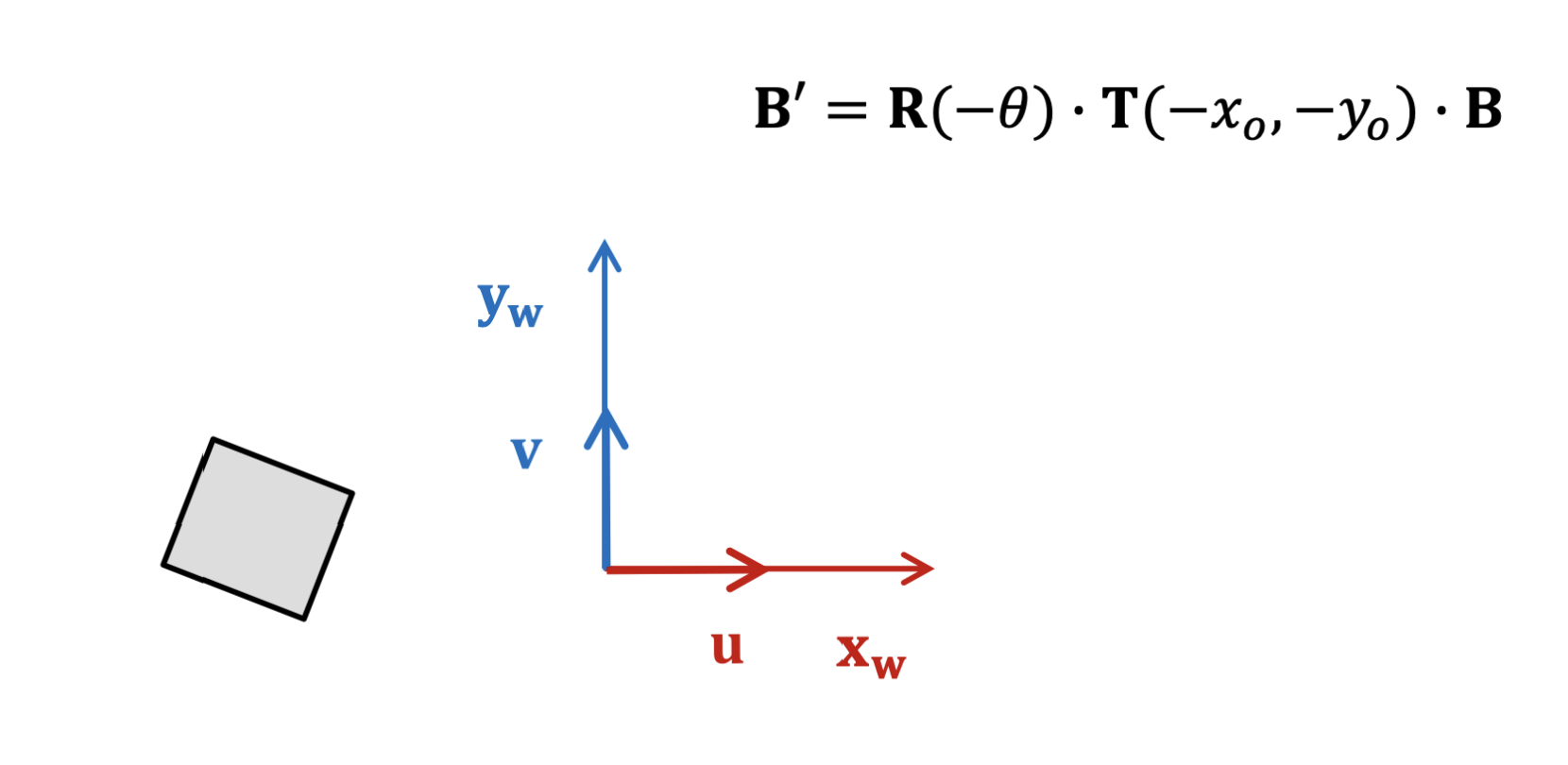
231209-235416

그리고 view coordinate를 rotation 하여 축을 일치시킵니다.

위 과정은 하나의 행렬로 표현 가능합니다.

B' = \begin{bmatrix} u_x & u_y & 0 \\ v_x & v_y & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -x_o \\ 0 & 1 & -y_o \\ 0 & 0 & 1 \\ \end{bmatrix} \cdot B

여기서 회전 방향이 시계방향이기 때문에 회전 백터가 Row 벡터로 이루어짐을 알아둡시다.

Projection

좌표를 이동했다면, 3차원 물체를 2차원 View plane에 투영(projection)해야 합니다.
투영하는 방법에는 소실점이 있는 Perspective projection과 소실점이 없는(무한한 거리에 있는) Orthographic projection 2가지 방법이 있습니다.

Perspective projection

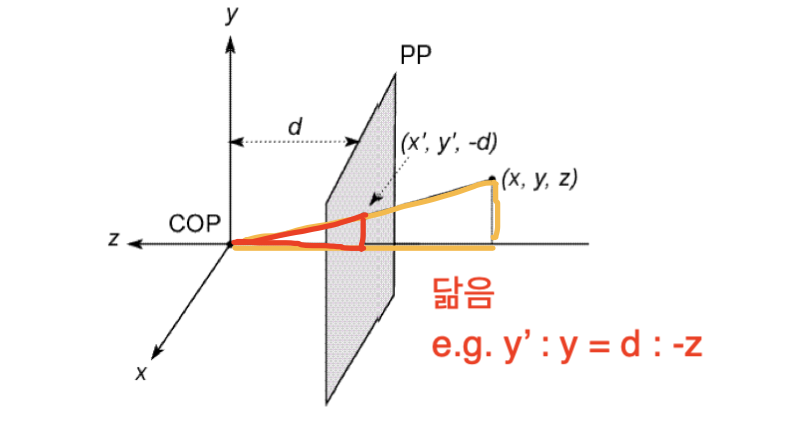
이 투영법은 닮음의 성질을 이용해서 투영합니다.
즉, 아래와 같이 좌표가 view space에서 view plane으로 변환됩니다.
$(x,y,z) \Rightarrow (-d\frac{x}{z}, -d\frac{y}{z})$
하지만, 이는 선형 변환이 아니므로, 계산의 효율을 위해 homogeneous coordinate로 변환하여 선형 변환으로 만들어줍시다.
$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1/d & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \\ y \\ -z/d \end{bmatrix}$
여기서 결과로 나온 벡터의 모든 원소를 $-z/d$ 로 나눠주면 $(-d\frac{x}{z}, -d\frac{y}{z})$ 를 얻을 수 있습니다.
(homogeneous coordinate의 사용 안하는 좌표를 1로 바꿔주는 연산과 동일합니다)

컴퓨팅 능력을 끌어올리기 위해 정사각행렬로 변환하면 식을 아래와 같이 표현할 수도 있습니다.
$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & -1/d & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ -z/d \end{bmatrix} \Rightarrow (-d\frac{x}{z}, -d\frac{y}{z})$
Orthographic projection

이 방식은 그저 z축의 정보을 사용하지 않으면 알아서 투영될 것입니다.
$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \Rightarrow (x, y)$

Clipping & Normalize

View Frustum

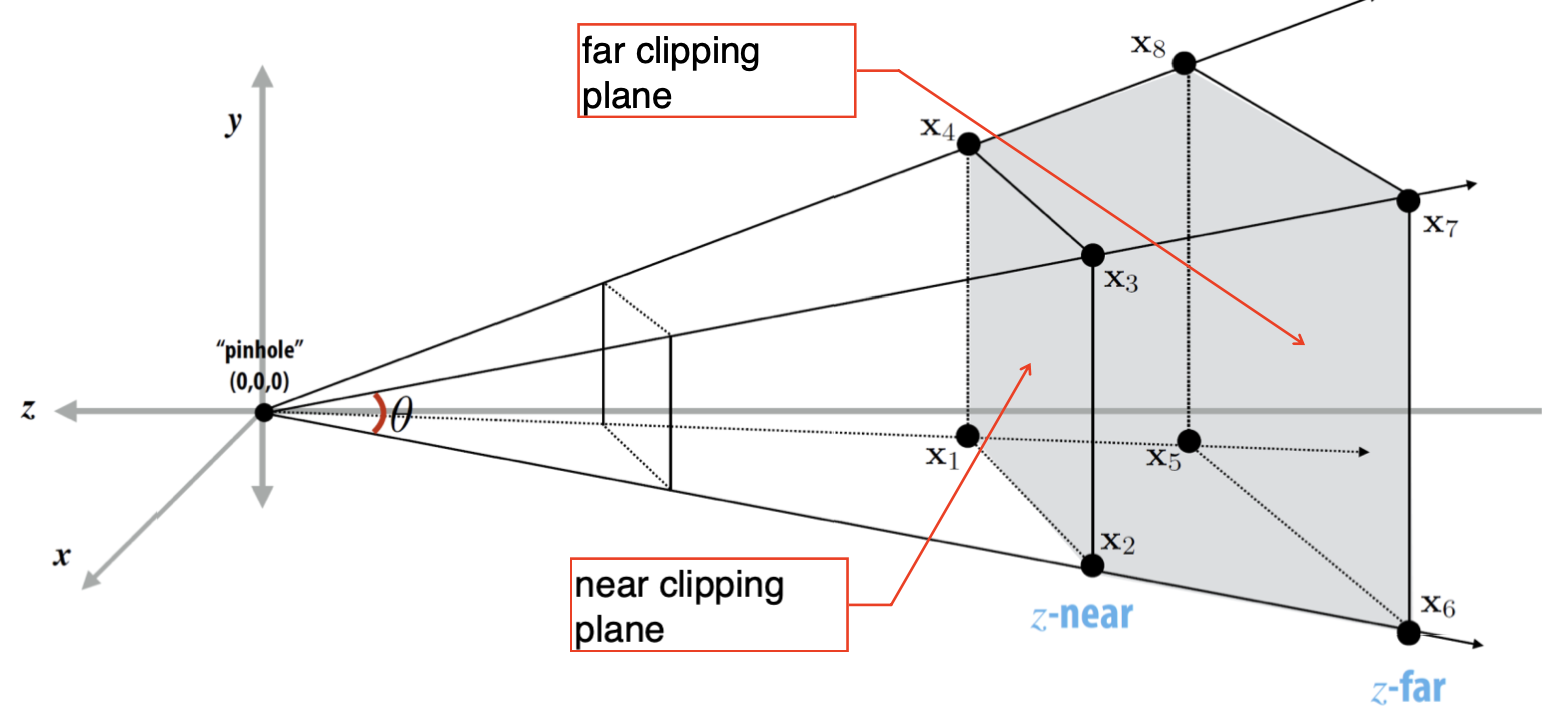
231210-001840
공간상에서 화면에 실질적으로 보여지는 영역을 의미하며, 절두체 형식으로 공간이 잘리게 됩니다.
최소로 카메라에 인식되는 평면을 near clipping plane, 최대는 far clipping plane 이라고 합니다.

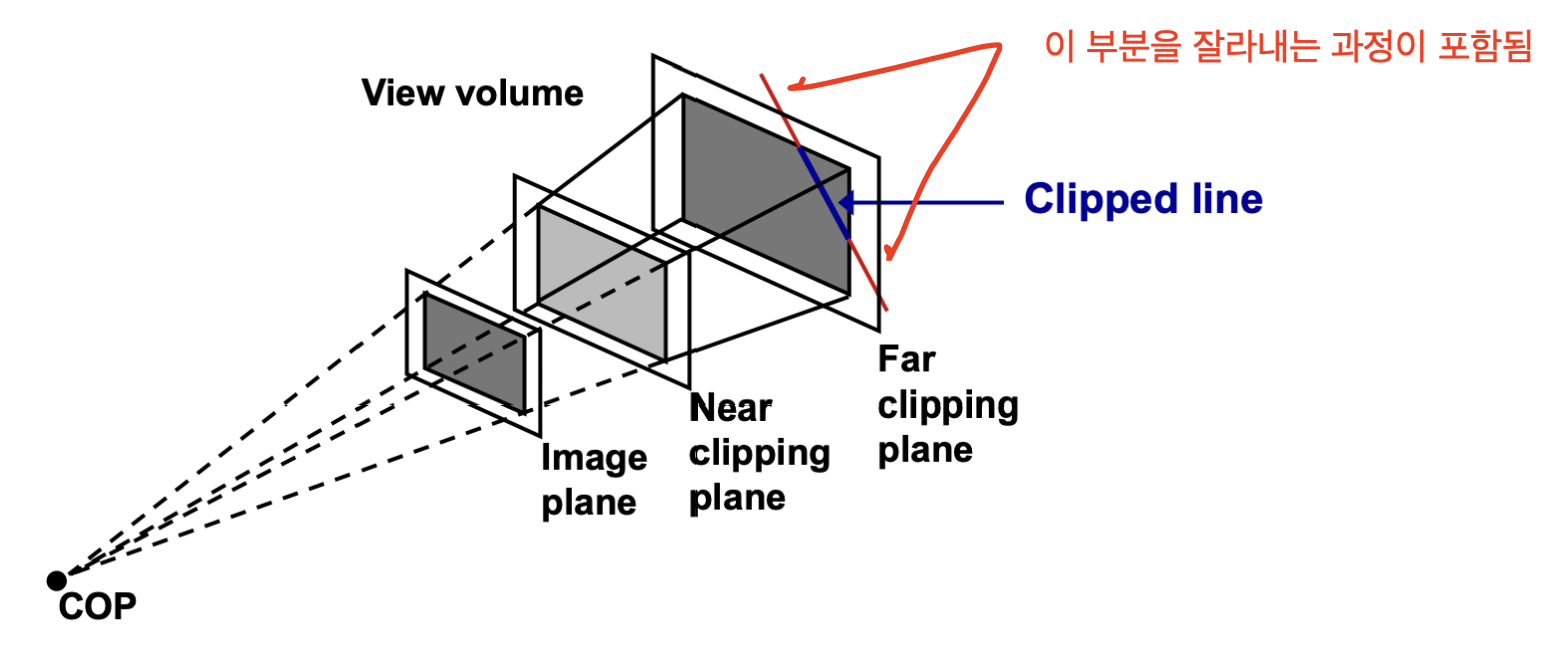
231210-002108

화면에서 보이지 않는 영역은 랜더링하지 않기 위해 clipping 하는 과정이 필요합니다.

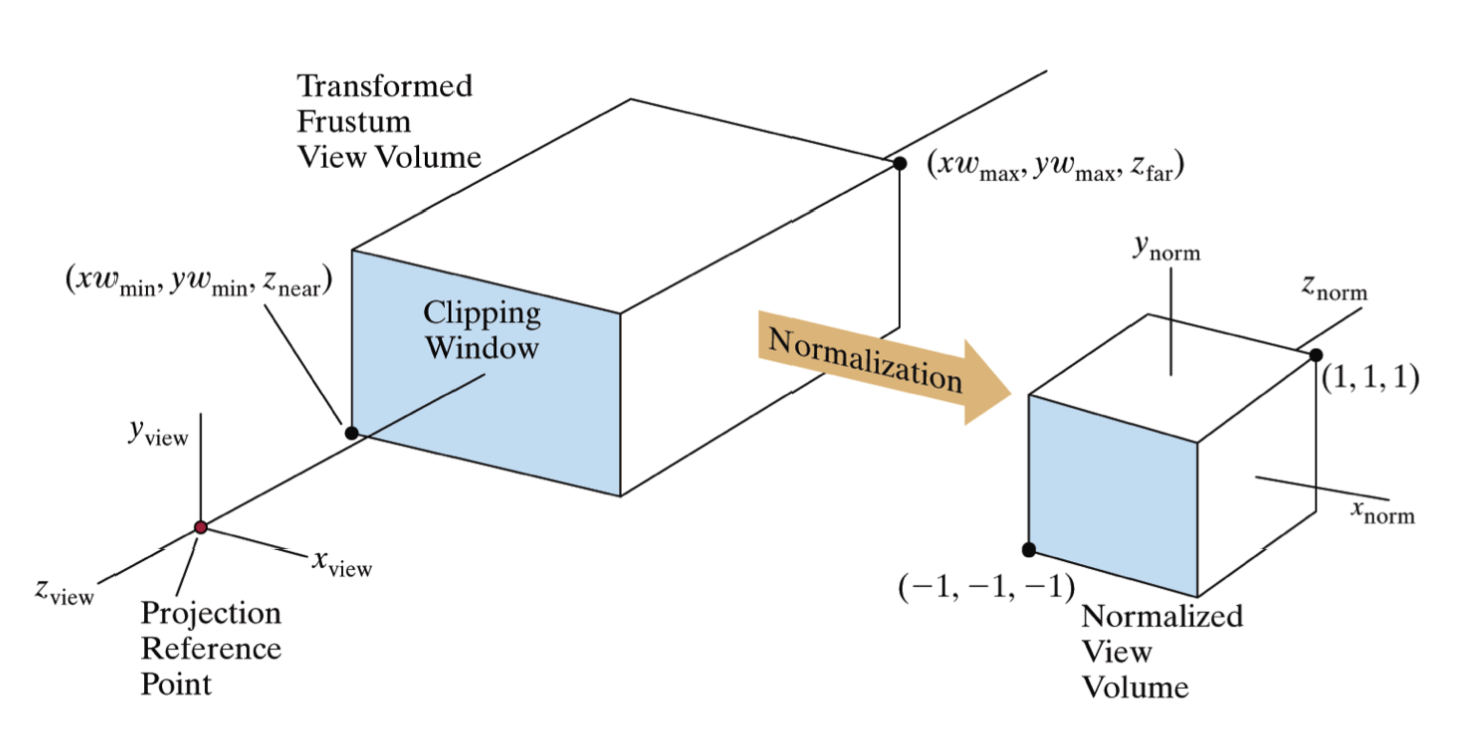
231210-002343

하지만, 절두체는 계산하기가 힘들기 때문에 near clipping plane을 확장시켜 정사각형으로 만들어준 뒤 clipping 과정이 들어가게 됩니다.

이후에는 모니터의 해상도에 맞게 변환을 편리하게 하기 위해 좌표를 [-1, 1] 사이로 normalize 하는 과정이 추가됩니다.

아래는 위의 모든 과정을 요약한 Geometry processing 과정입니다.

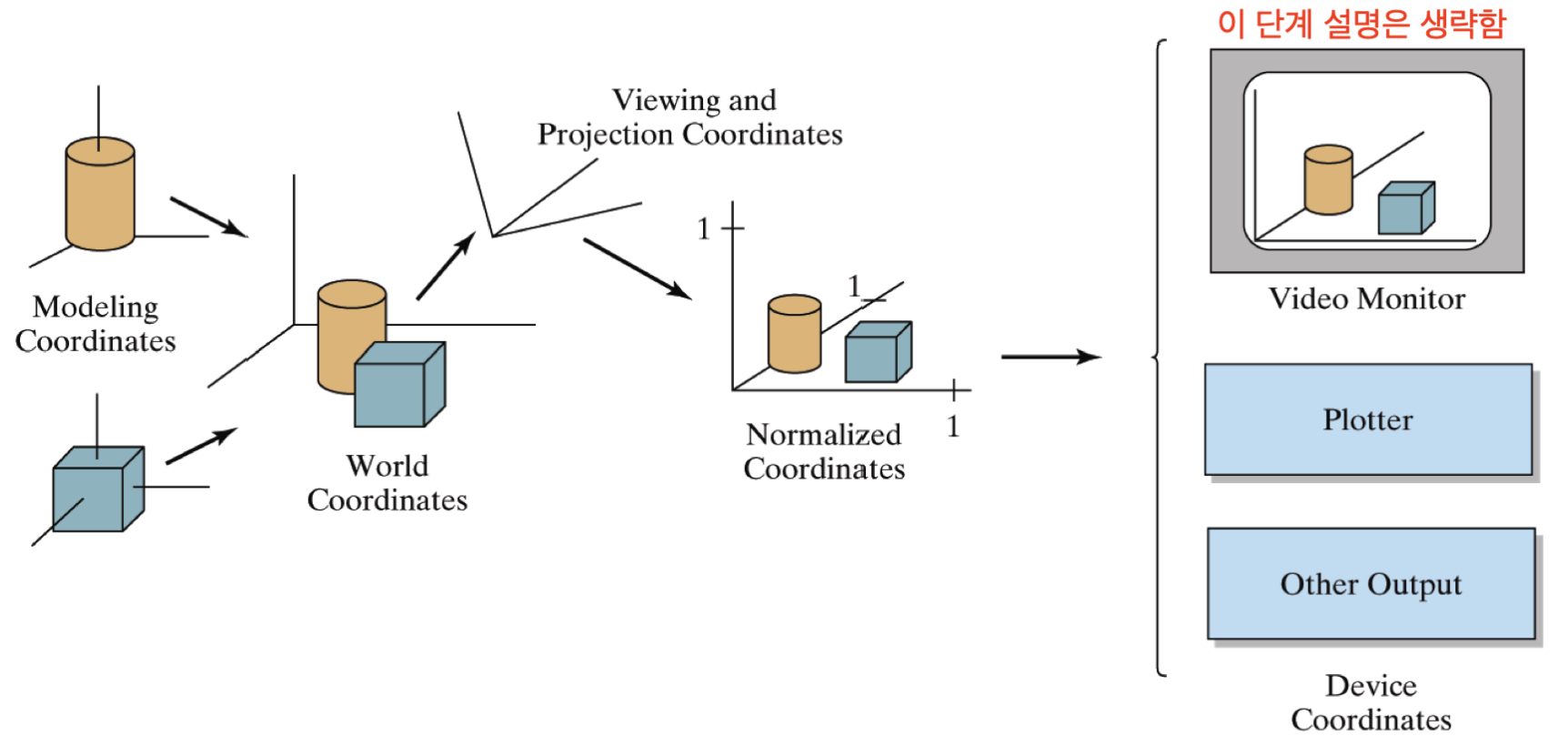
231210-002534

Lighting and shading

이 단계 역시 Geometry processing 단계에서 수행되지만, 분량이 많으므로 별도로 다뤄보겠습니다.

빛을 인식한다는 것은 광원으로부터 나온 빛이 물체와 부딪혀 흡수되지 않은 반사된 빛을 눈이 감지하는 과정을 의미합니다.
하지만 빛의 진행과 반사를 모두 추적하는 것은 연산량이 매우 많이 필요하기 때문에 이를 단순화 하기 위해 광원의 종류와 반사의 종류를 나누어 연산합니다.

Light sources

광원의 종류에 따라 광원을 수식으로 표현해보겠습니다.

색상을 표현하기 위해 RGB값을 모두 연산해야 하지만, 수식으로 나타낼 때는 벡터 I로 한 번에 표현합니다.

I = \begin{bmatrix} I_R \\ I_G \\ I_B \\ \end{bmatrix}

Point lights

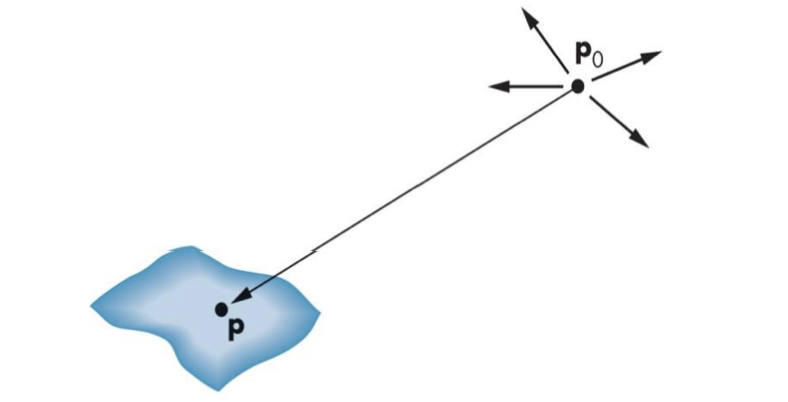
점광원으로 일반 적인 광원입니다.
빛의 강도는 거리의 제곱에 반비례하며, 수식적으로는 아래와 같이 표현됩니다.
$I(p, p_0) = \frac{1}{|p-p_0|^2}I(p_0)$
하지만, 이렇게 처리하는 경우 실제로 거리에 따른 표현이 잘 되지는 않습니다.
따라서 제곱항만 넣는 것이 아닌, 다항식으로 처리됩니다.
$I(p, p_0) = \frac{1}{k_c + k_ld + k_qd^2}I(p_0)$
Distant lights

방향성 광원(무한히 멀리있는 광원)으로, 점광원과 차이점은 위치를 고려하지 않는다는 점입니다.
점광원은 위치에 따라 입사각이 달라졌다면, 방향성 광원은 방향에 따라서만 입사각이 달라지게 됩니다.
위 식에서 $p_0$ = [x y z 1] $^T$ 였다면, 방향성 광원에서는 $p_0$ = [x y z 0] $^T$ 입니다.
Spotlights

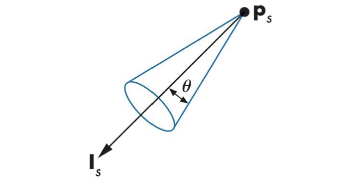
점광원 + 원뿔로, 점광원과 비슷하지만, 원뿔 영역에 해당하는 부분에만 빛이 비춰집니다.
수식적으로 아래와 같습니다.
$I = cos^e \phi = (s\cdot I_s)^e$
여기서 $\phi$ 는 0과 $\theta$ 사이의 값이고, e값이 커질수록 중심부가 강하게 스포트라이트 됩니다.
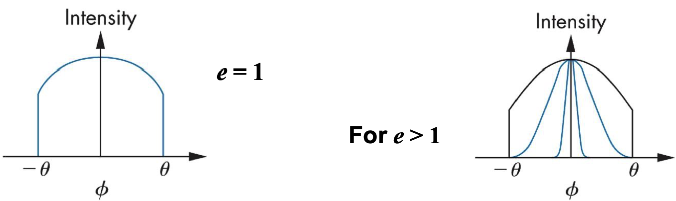
Ambient lights

배경 광원으로 공간 전체에 은은하게 퍼져있는 빛입니다.
즉, Intensity만 전체적으로 더해주면 됩니다.

Interaction with Materials

빛과 상호작용하는 물질에 따라 흡수, 투과, 반사되는 정도가 달라지는데 여기선 반사에 대해서만 다뤄보도록 합니다.
(반사를 해야 물체가 눈에 보이겠죠?)

반사는 Phong reflection model로 표현되는데 이는 정반사(Specular) + 난반사(Diffuse) + 배경 의 3요소로 표현됩니다.
하나하나 알아봅시다.

Ambient reflection

배경 반사는 물리적 실체가 있는 구성요소는 아니고, 랜더링시 전체적으로 퍼진 빛을 시뮬레이션하기 위해 계산하며 아래와 같습니다.
$I_a = k_aL_a$
여기서 $k_a$ 는 반사 계수로 0과 1 사이의 값을 가지며, 1이면 배경 빛을 모두 반사합니다.
Diffuse reflection

난반사는 빛의 입사각과 관계 없이 모든 방향으로 반사한다고 가정하기 때문에 입사하는 빛의 양만 알면 반사량을 계산할 수 있습니다.
$I_d = k_d(N\cdot L)L_d$
여기서 N은 표면의 수직 단위벡터, L은 빛 소스( $L_d$ ) 로의 방향 단위벡터 입니다.
즉, 사이각을 계산하는 항이 추가된 것입니다. (Position dependent)
Specular reflection

정반사는 입사각과 동일한 반사각으로 빛을 반사합니다.
즉, 관찰자가 어디있는지에 따라 반사된 빛의 밝기가 다르게 느껴지게 됩니다. (View, Position dependent)
$I_s = k_s(cos\alpha)^nL_s = k_s(V\cdot R)^nL_s$
여기서 R은 반사되는 방향 단위벡터, V는 view 방향 단위벡터 입니다.
또한 $\alpha$ 는 R, V 사이의 각도입니다.

또한 n은 일종의 상수인데, 거울의 경우에는 n이 거의 무한한 값이고, 금속은 100~500 사이 정도로 표현됩니다.

Polygonal Shading

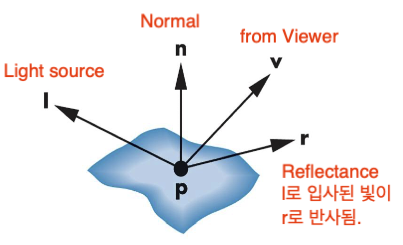
231211-170419

지금까지 위 그림과 같이 빛을 반사까지 했습니다.
그렇다면 이제 폴리곤 덩어리에 색칠을 해야 하는데, 그 방식도 여럿 존재합니다.
각 방식과 장단점을 알아봅시다.

Flat shading

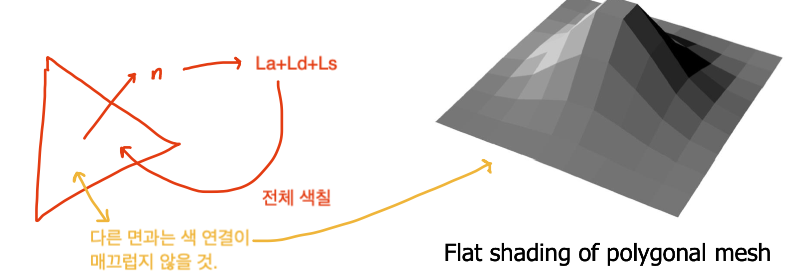
면 단위로 색칠하는 방식으로 특정 면의 법선 벡터 n을 구하면 해당 면을 하나의 색상으로 칠하는 방식입니다.
계산량은 가장 적지만, 다른 면과 매끄럽게 연결되지 않는다는 단점이 있습니다.
Gouraud shading

vertex 단위로 색칠하는 방식으로 면의 꼭짓점의 법선 벡터들을 구하고, 꼭짓점들의 색상을 칠합니다.
면의 내부는 꼭짓점의 색상을 선형 보간하는 방식으로 계산합니다.

이 때, 꼭짓점은 점이기 때문에 법선 벡터를 바로 구할 수는 없습니다.

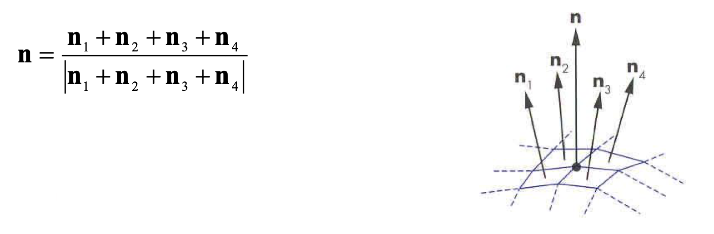
따라서 개발자가 임의로 지정해주거나, 주변 면의 법선 벡터의 평균을 사용해서 구하는 방식을 사용합니다.

계산량은 보통이지만, 면과 면이 부드럽게 연결됩니다.
하지만, vertex의 보간으로 계산하기 때문에 면 중앙에만 하이라이트로 비춰지는 빛을 표현할 수는 없습니다.
Phone shading

픽셀 단위로 색칠하는 방법으로 꼭짓점의 법선 벡터를 구하는 것 까지는 동일합니다.
하지만, 색칠을 할 때는 픽셀별로 법선 벡터를 선형 보간하는 방식으로 구한 후, 픽셀의 법선 벡터를 이용해서 색상을 칠합니다.

따라서 계산량은 가장 많지만, 가장 사실적으로 빛을 묘사할 수 있습니다.

물론, 반사되는 빛 표현만 사실적으로 하는 것이지, 실루엣까지 부드럽게 할 수는 없습니다.
실루엣을 부드럽게 하려면 vertex 개수 자체를 늘리는 방법을 사용해야 합니다.

Rasterization

모든 객체는 아래의 세가지의 조합으로 표현할 수 있습니다.

Points
Line segments
Triangles

예로 들어 곡선은 짧은 직선을 어려개로 근사할 수 있고, 폴리곤 덩어리와 곡면 역시 여러 삼각형으로 근사할 수 있습니다.

하지만, 위 세 요소를 수학적으로 기술했다고 해도, 화면에 띄우는 과정에서 Aliasing 현상이 나타나게 됩니다.

선을 기준으로 여러 근사 알고리즘과 Aliasing 현상을 알아보도록 합시다.

Point Sampling

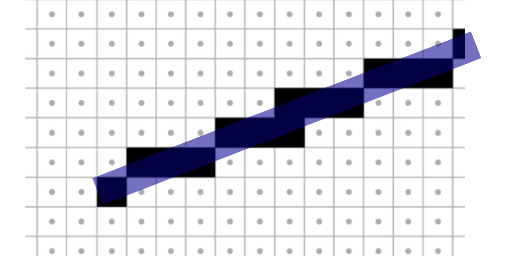
각 픽셀의 중심부가 직선 범위 내부이면 1, 아니면 0으로 처리합니다.
연산량이 가장 적이만 문제가 많습니다.
Bresenhan Line

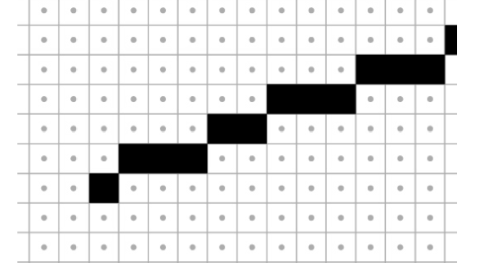
인접한 픽셀이 둘 다 켜지는 방식을 방지하는 알고리즘으로, row, column 별로 1개만 1이 되도록 강제합니다.
Box Filtering - Antialiasing

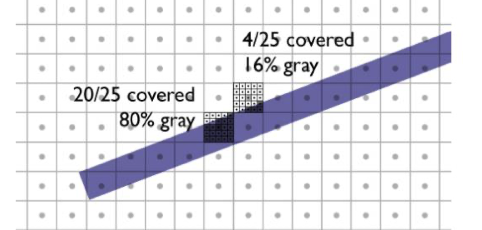
각 픽셀이 직선에 얼마나 포함되는지에 대한 정보를 바탕으로 [0, 1] 사이로 찰하게 합니다.
Antialiasing이 아닌 방식에 비해서는 느리지만, 그래도 빠른 편이며, 나름 정확하게 표현할 수 있습니다.
Weighted Filtering - Antialiasing

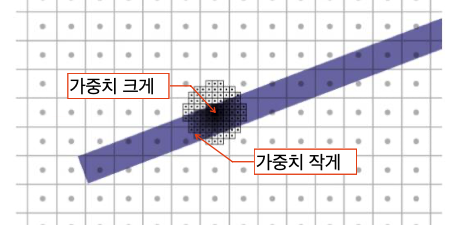
가우시안 필터링 기법을 사용하여 가중치를 부여(중심부의 weight가 큼)한 평균을 계산하여 칠합니다.
가장 느리지만, 가장 묘사가 잘 됩니다.

Hidden Surface Elimination

시각에 따라 보이지 않는 폴리곤 덩어리를 랜더링하면 성능이 떨어질 것입니다.
따라서 보이지 않는 부분은 랜더링 대상에서 제외시키는 방법들을 알아봅시다.

Back-face Culling

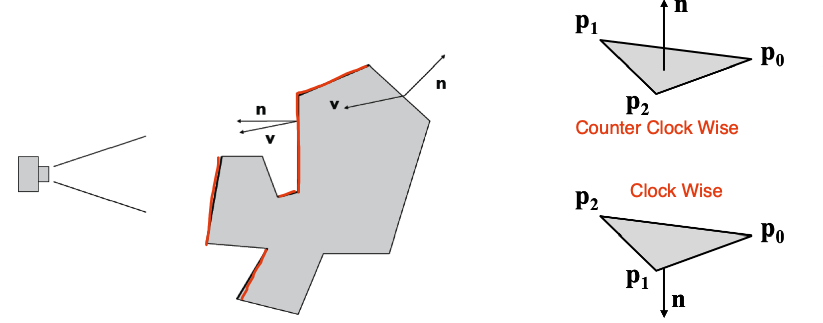
간단하게 설명하면 뒤를 바라보는 면은 랜더링 대상에서 제외시키는 방법입니다.
view 방향 단위벡터(v)와 면의 법선 단위벡터(n)를 이용해서 $n \cdot v$ 로 계산하여 양수라면 랜더링, 음수면 제외하는 방식으로 동작합니다.

주의할 점은 법선 벡터를 계산할 때, 꼭짓점의 좌표를 이용해서 $(p_1-p_0) \times (p_2-p_0)$ 와 같이 계산해야 하는데, 시계방향, 반시계방향으로 죄표를 넣으면 법선 벡터의 방향이 달라지게 됨을 주의합시다.
Depth Buffer (Z-Buffer)

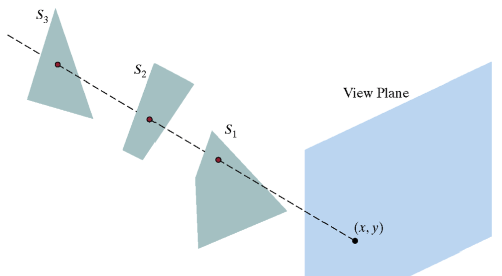
진짜 무식한 방법이지만, Back-face culling보다 성능 좋은 방법입니다.
1. 우선, Z-buffer를 무한대로, Frame buffer를 배경색으로 초기화 합니다.
  $Z(x,y) = \infty \\ C(x,y) = c_0$
2. depth가 작아지면, 즉 더욱 view plane에 가깝다면 (z(x, y) < Z(x, y)) Z, Frame buffer를 업데이트 합니다.
  $Z(x,y) = z(x,y) \\ C(x,y) = c(x,y)$
심지어 속도도 빠릅니다.
하지만, 메모리를 많이 쓴다는 단점은 있습니다.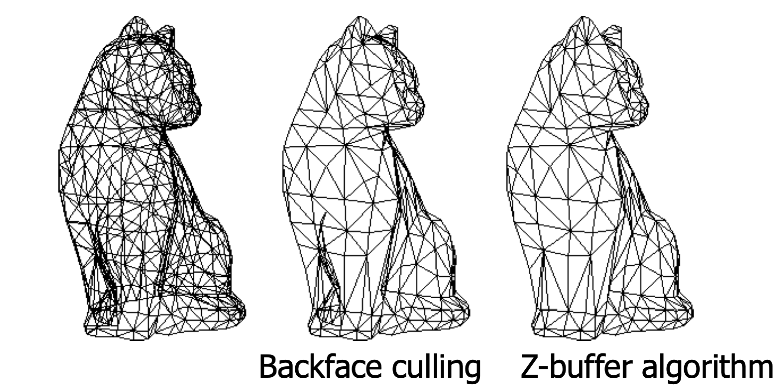

하지만 오늘날은 메모리 용량도 많기 때문에 Z-Buffer 방식을 사용합니다.

Texture mapping

간단하게 텍스쳐를 폴리건 표면에 붙이는 방법만 알아봅시다.

폴리건에 붙이고자 하는 텍스쳐 이미지를 [0, 1]로 normalize 합니다.
world coordinate(폴리건)과 texture coordinate(텍스쳐)의 대응관계를 찾습니다.
대응관계에 따라 normalize된 텍스쳐의 좌표를 변환하여 폴리건 위에 씌웁니다.

일부 수학적 3차원 도형의 경우 2개의 좌표로도 표현이 가능한데, 이를 텍스쳐 좌표에서 활용하면 됩니다.

이 과정에서 샘플링이 누적되며 오류가 중첩되어 Aliasing 현상이 발생할 수 있습니다.

또한, 텍스쳐를 이용해서 세부 음영 묘사를 할 수 있는 트릭을 사용할 수 있습니다.
즉, 폴리건은 간단히 만들고, 세부 음영 묘사는 텍스쳐로 수행하여 성능을 높이는 최적화 방법입니다.

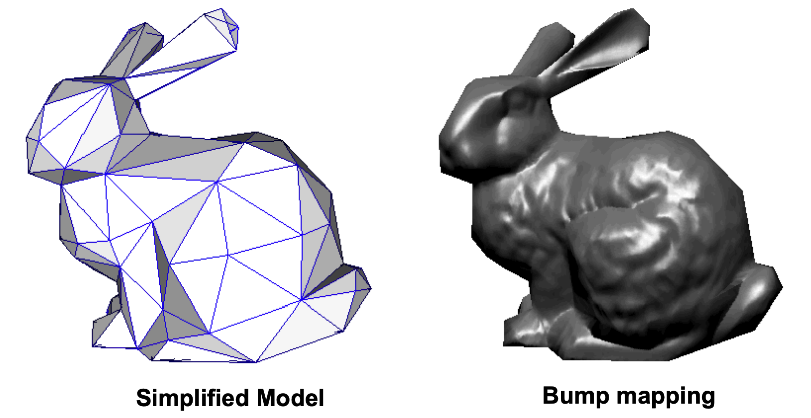
231211-174923

하지만, 가장자리 실루엣은 세부적으로 묘사가 안됩니다.
(vertex를 늘리는 방법 외엔...)

마지막으로, 배경을 텍스쳐로 입혀서 반사를 구현하는 최적화 방식 또한 있습니다.