Vector
벡터에 대한 기본적인 내용에 대해 다뤄봅니다.읽는데 6분 정도 걸려요.Vector와 Points는 (1, 2, 3) 과 같이 숫자로된 좌표로 표현된다는 점에서는 비슷하다.
하지만, Points는 공간의 위치를 나타내지만, Vector은 방향과 크기를 나타낸다는 점이서 다르다.
(벡터는 위치 개념이 없음. 상대적인 방향과 크기만을 가질 뿐)
Vector Algebra
Scalar Multiplication
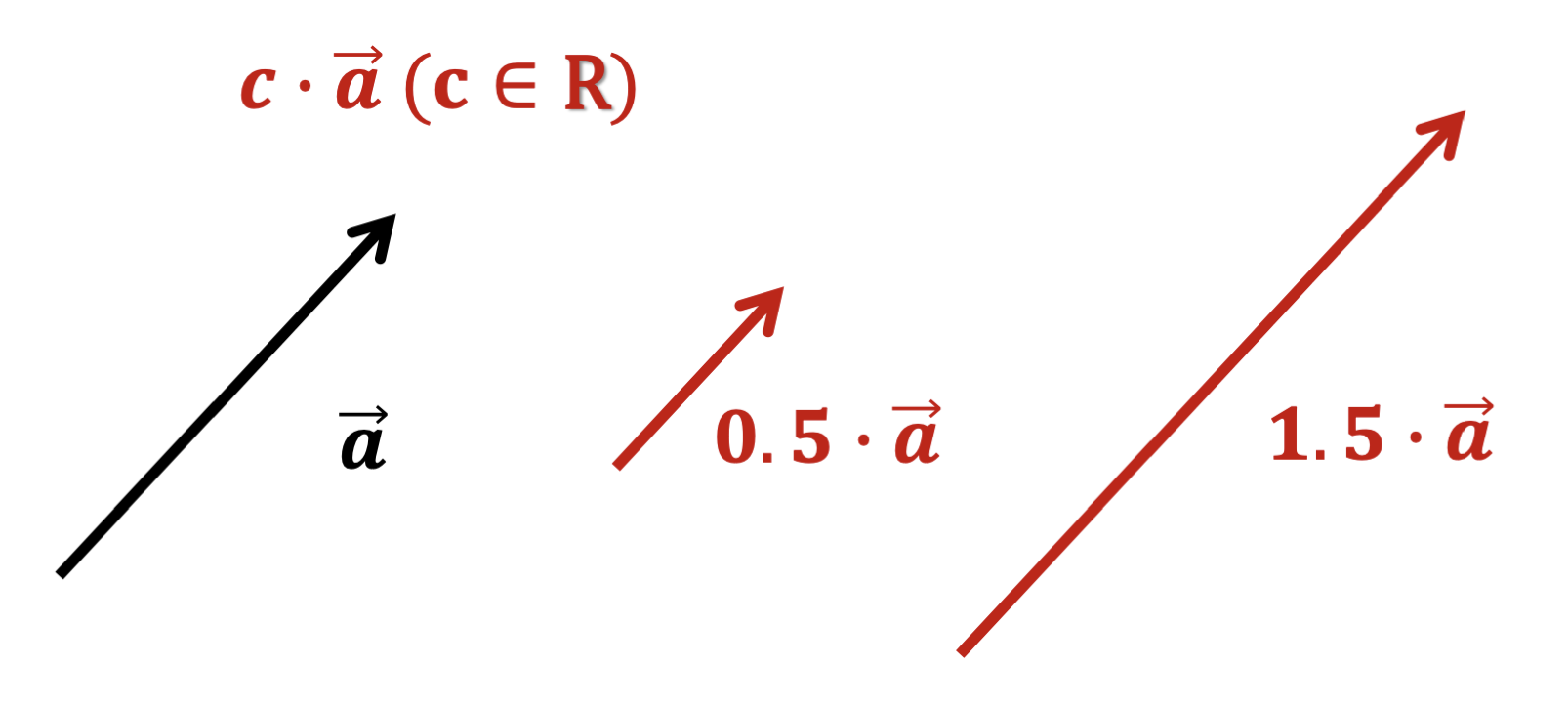
해당 방향으로 크기만 증가하는 연산이다.
벡터의 각 성분에 크기 c만큼 각각 곱해주면 된다.
Addition
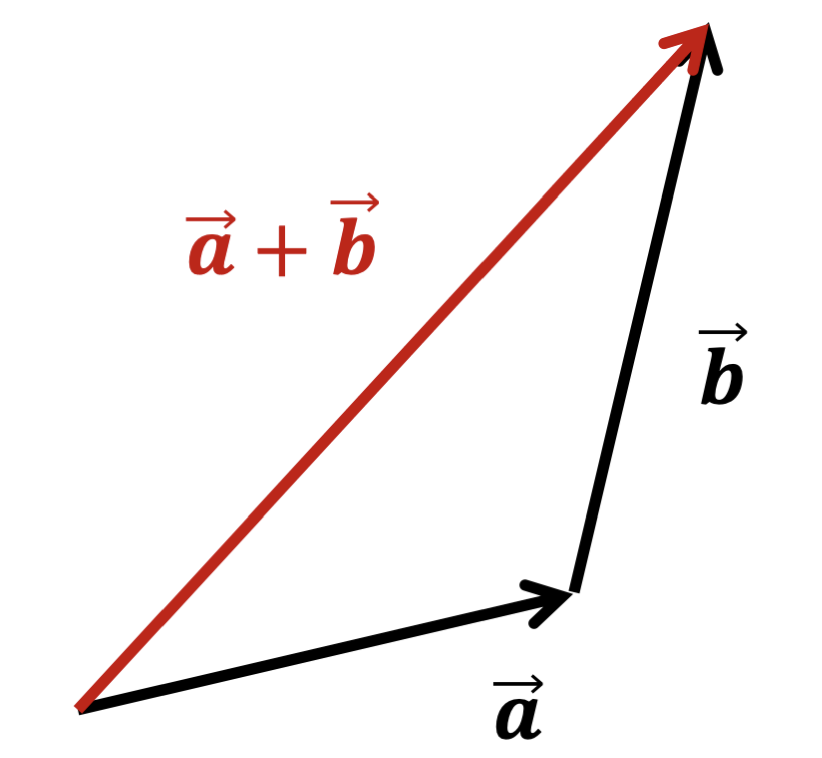
A 벡터의 종점에 B 벡터의 시점을 이어붙이는 연산으로, 그 값은 A 벡터의 시점 → B 벡터의 종점이 된다.
평행 사변형법으로도 계산할 수 있으며, 벡터의 각 성분끼리 더하면 된다.
Substraction
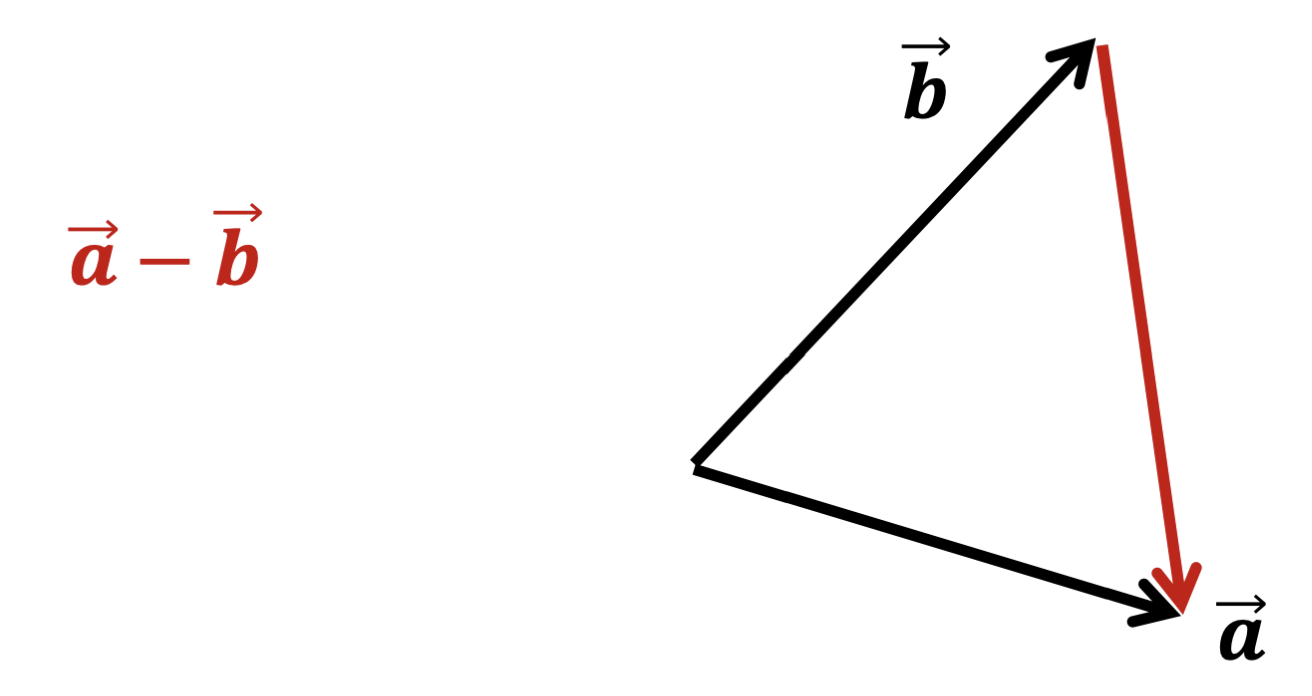
벡터에 -1을 스칼라 곱을 한 후, Addition을 한 결과와 같은 연산이다.
벡터의 각 성분을 빼주면 된다.
Length & Direction
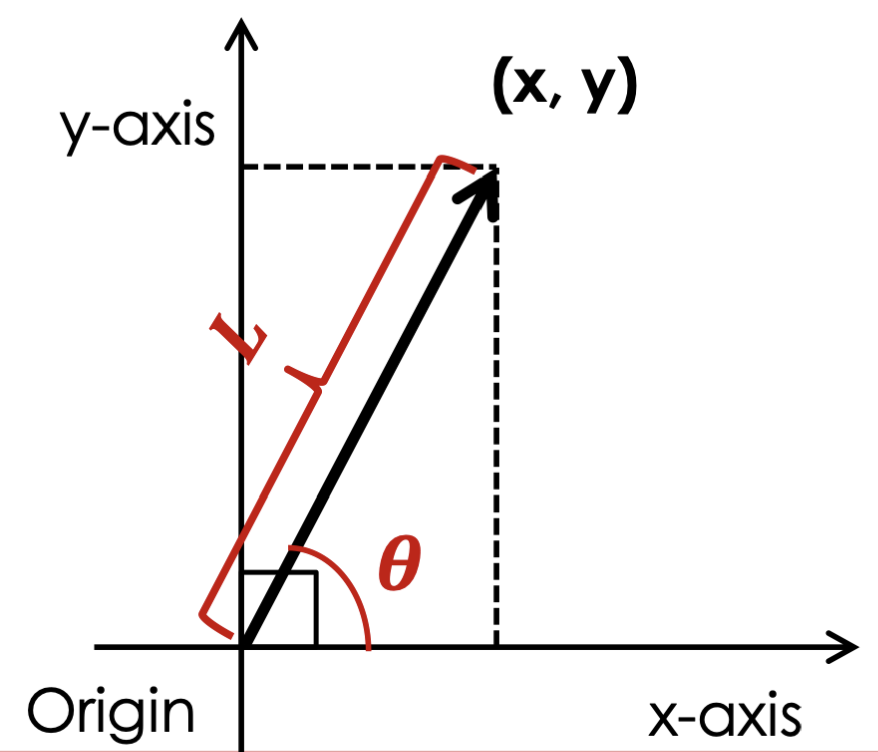
벡터의 크기()와 x축에 대한 방향()는 다음과 같다.
크기가 1인 벡터를 단위벡터 라고 하며, 벡터를 단위벡터로 변환하는 것을 Normalization 이라고 한다.
백터를 Normalization 하는 법은 벡터의 각 성분을 로 나눠주면 된다.
Linear Combination
벡터들을 선형결합 하는 것을 의미한다.
이는 , , ..., 의 선형 결합이며, 상수 c를 weight라고 부른다.
이 weight 값에 따라 다른 명칭으로 불리기도 한다.
-
Affine Combination
weight의 합이 반드시 1이 되는 선형결합. -
Convex Combination
weight이 모두 양수이고, 합이 반드시 1이 되는 선형결합.
Dot product (내적)
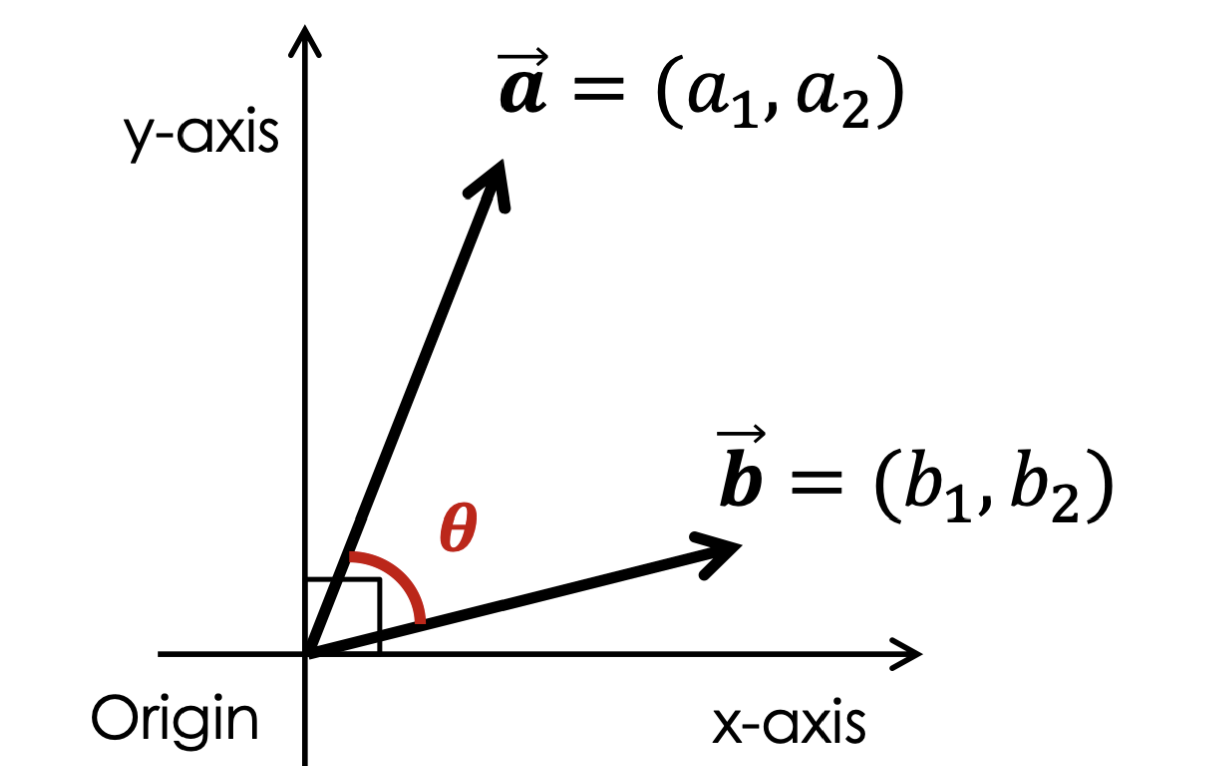
내적의 연산 결과는 스칼라가 되는데 우선 식부터 살펴보자.
내적은 사잇각을 알아내는데 사용할 수 있는데, 그런데 내적 그 자체는 무슨 의미를 가질까?
유닛벡터에 대해 다음과 같은 내적값은 다음과 같은 의미를 갖는다.
-
1
두 벡터가 같은 방향으로 평행하다 -
-1
두 벡터가 정 반대 방향으로 평행하다 -
0
두 벡터가 수직한다 -
>0
두 벡터가 같은 방향이다 -
<0
두 벡터가 다른 방향이다
Projection
내적을 응용하면 한 벡터를 다른 벡터에 사상한 벡터를 얻을 수 있다.
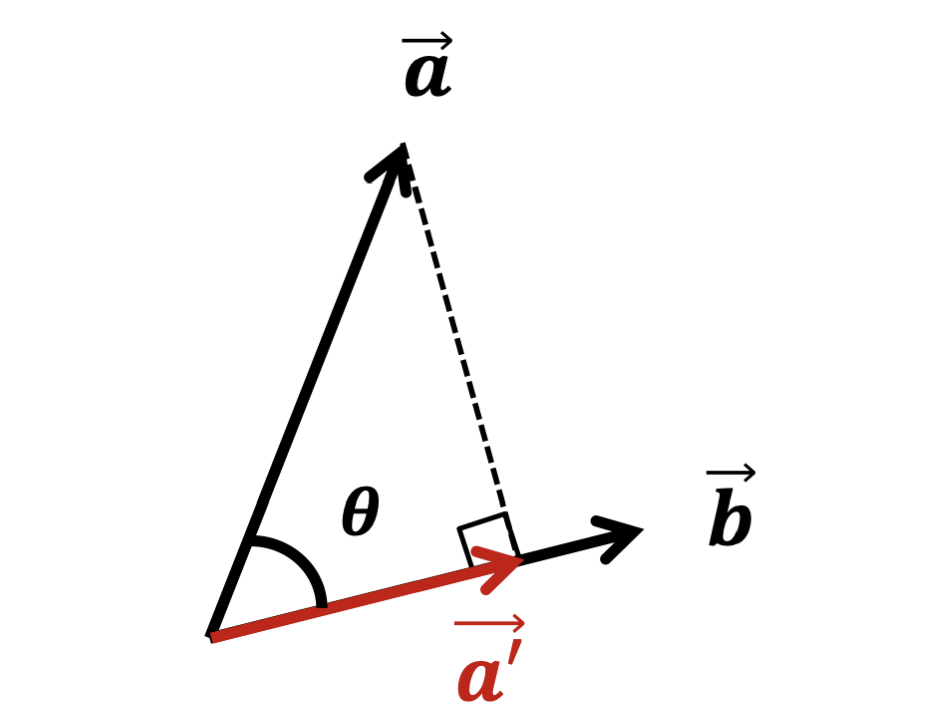
벡터의 길이는 와 같다.
또한 벡터의 단위벡터는 이다.
따라서 둘을 곱한 다음의 식이 벡터 a를 벡터 b에 사상한 벡터가 된다.
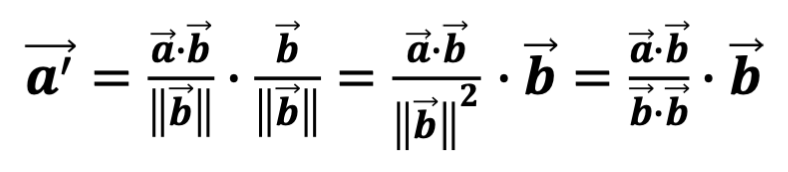
Cross produce (외적)
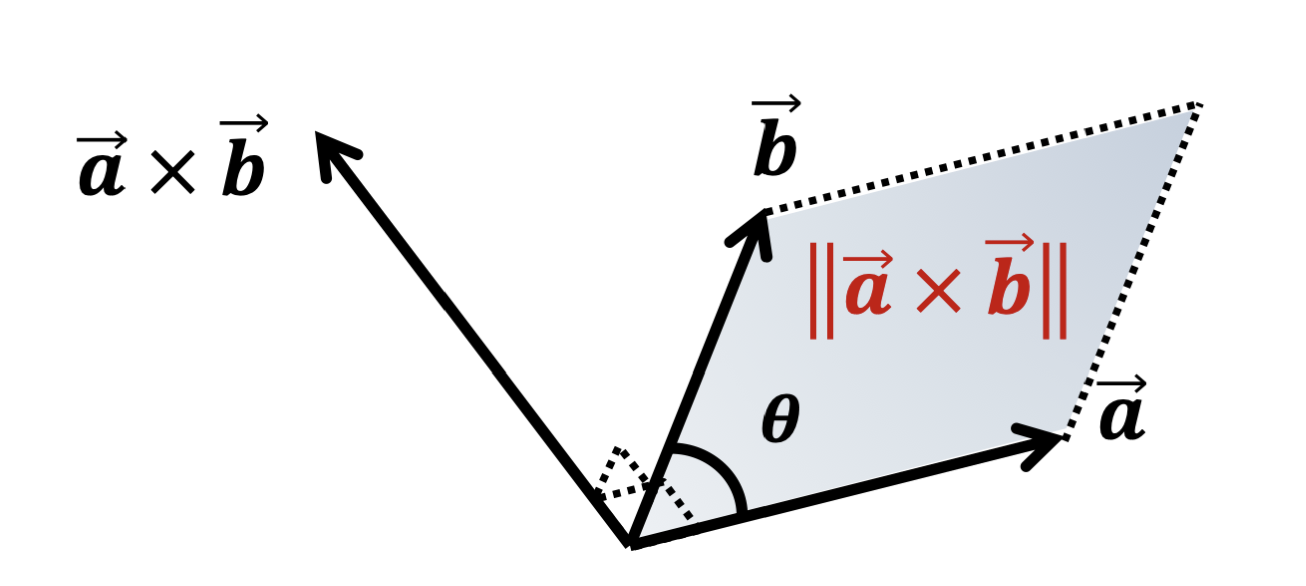
여기서 은 벡터 a, b에 수직한 유닛 벡터
외적 두 벡터의 수직인 벡터로, 그 크기는 두 벡터가 이루는 평행사변형의 넓이이다.
계산은 아래와 같이 하면 된다.
Normal Vector
한 평면에 대한 수직 단위벡터로 외적을 이용하면 구할 수 있다.
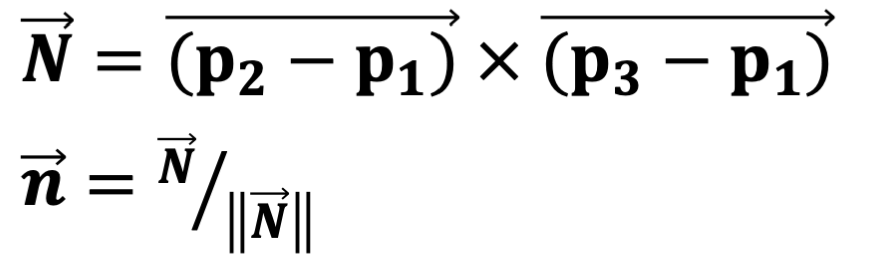
Points Algebra
Points 는 더하거나, 스칼라곱에 대한 정의가 없다.
하지만, 특수 상황에서는 의미를 갖는데, 그것들에 대해 알아보자.
Point - Point
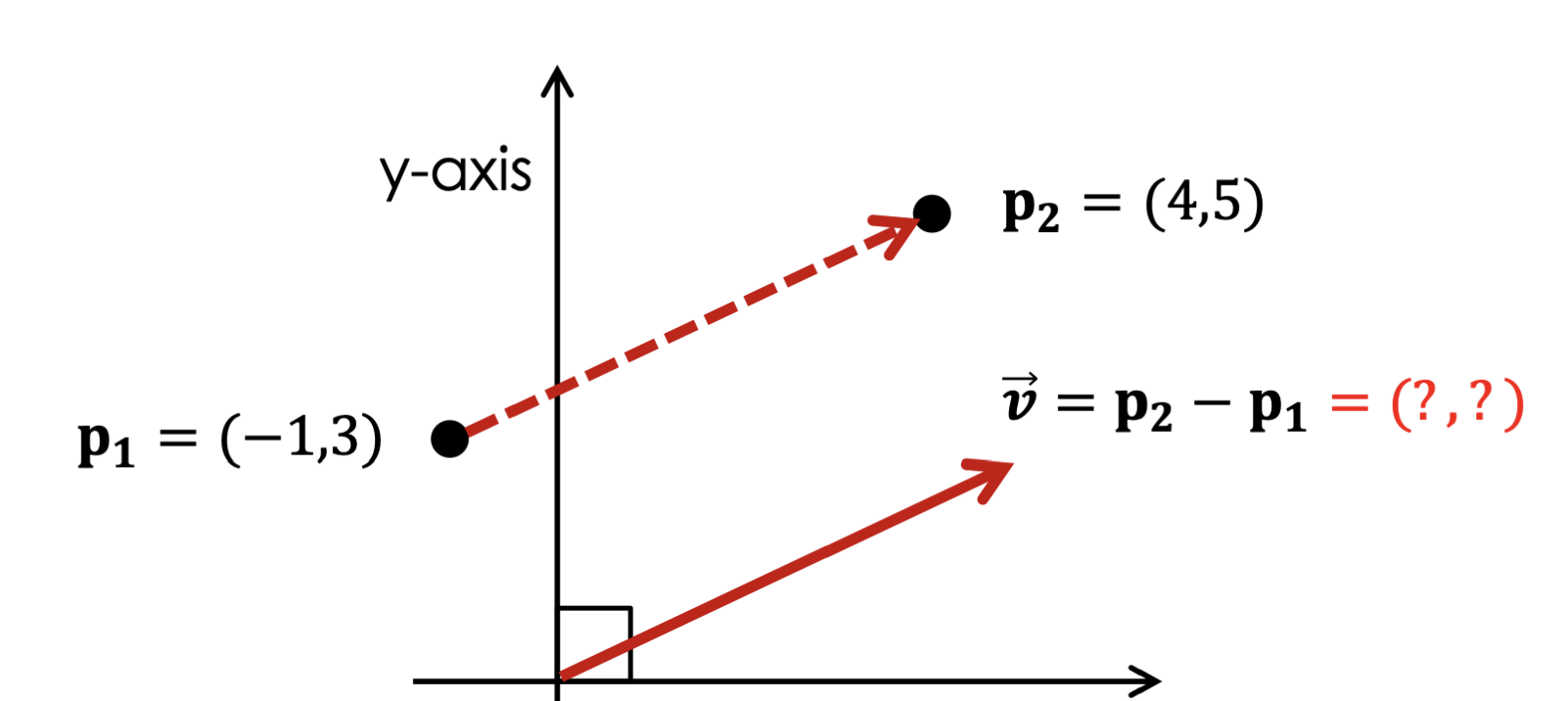
Point B에서 Point A를 뺴면, 그 결과는 A→B Vector가 된다.
Point + Vector
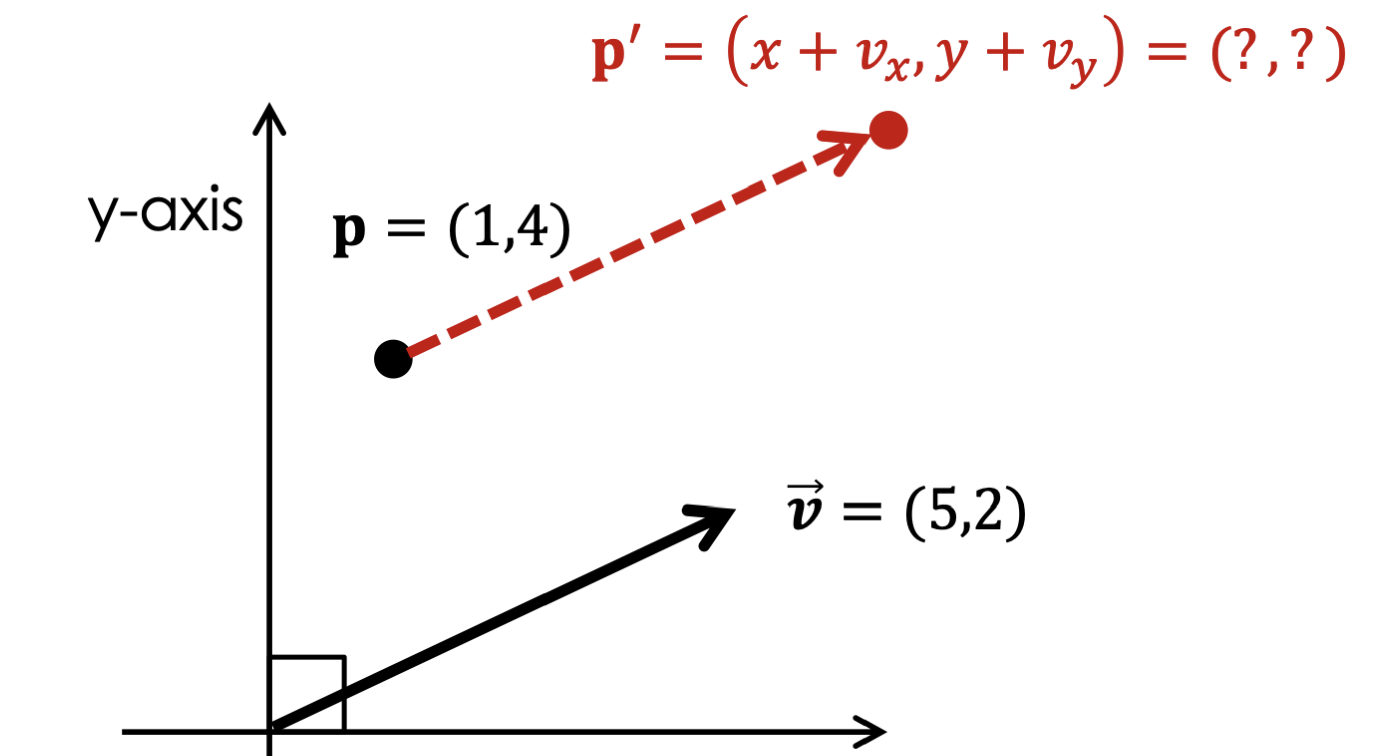
Point에 Vector를 더하거나 빼면 다른 Point가 된다.
Affine Combination
위에서 언급했 듯, Points 는 더하거나, 스칼라곱에 대한 정의가 없다.
하지만, 스칼라 곱 중에서 그 weight의 합이 1이 되는 경우 내분, 또는 외분의 의미를 갖게된다.