🫧

AI

게임에서의 AI, 그 중 pathfinding 방식에 대해 알아봅니다.읽는데 11분 정도 걸려요.

Basic Pathfinding

경로 찾기 알고리즘을 평가하는 요소는 다음과 같습니다.

  • 해가 존재하는 문제에 대해 해를 구할 수 있는가? (Complete)
  • 최적해를 보장할 수 있는가? (Optimal)
  • 시간, 공간 복잡도가 복잡한가? (Time, Space)

여러 알고리즘을 알아보며 평가해봅시다.

Greedy

당장의 이득이 큰 선택을 이어가는 방식입니다.
예로 들어 현재 위치에서 목적지 까지의 거리가 최소화되는 방향으로 이동하는 방식이 그리디 정책입니다.

하지만, 최적해를 보장하지 못한다는 문제가 있습니다.

BFS

그리디 방식보다는 Graph를 탐색하는 기법을 활용하는 것이 최적해를 찾을 수 있습니다.
그 중 Breadth First Search 방식은 최적해를 보장할 수 있습니다.

하지만, BFS는 모든 경로를 기록해야 하기 때문에 공간 복잡도가 높으며 시간 복잡도 또한 높게 측정됩니다.

vs. DFS
Depth First Search 방식은 일반적으로 BFS보다 시간, 공간 복잡도 측면에서 효율적입니다.
하지만, 이 역시 Greedy만큼 심각하지는 않지만, 역시 최적해를 보장할 수 없습니다.
또한, graph에 cycle이 존재하는 경우에는 해를 구하지 못하는 경우도 생깁니다.

AlgorithmCompleteOptimalTimeSpace
BFSYYO(min(N,BL))O(min(N, B^L))O(min(N,BL))O(min(N,B^L))
DFSYNO(BLMAX)O(B^{L_{MAX}})O(LMAX)O(L_{MAX})

vs. Greedy
그리디와 BFS는 사실 비슷합니다.
231211-215115

A*

위에서 BFS와 Greedy 방식이 비슷하다 했었는데, 다른 부분은 priority queue를 사용하는 것이 차이입니다.

그렇다면, BFS에서 먼저 pop되는 노드의 기준은 무엇일까요?
처음부터 현재까지의 탐색 거리 중 가장 짧은 거리를 g라고 했을 때, g가 가장 작은 노드가 선택되게 됩니다.

Greedy에서 먼저 pop되는 노드의 기준은 무엇일까요?
현재 지점부터 목표 거리까지 거리가 최소가 될 거 같은 휴리스틱한 거리를 h라고 했을 때, h가 가장 작은 노드가 선택되게 됩니다.

A*는 BFS와 Greedy의 장점만을 모은 알고리즘으로, f = g + h 라 했을 때, f가 가장 작은 노드를 선택하여 경로를 탐색합니다.
즉, 빠르게 탐색하면서도 최적해를 보장할 수 있게 됩니다.
하지만, 메모리를 너무 많이 사용한다는 단점도 있습니다.

의사 코드는 아래와 같습니다.

A*
INIT priority-queue Q
INSERT start node N to Q
while (Q is not empty) {
  REMOVE best N from Q that has lowest f(N)
  if (N is goal) break
  for (next node N' in Succ(N)) {
    if (N' is visited first ||
        previously expanded with f(N') > f(N) ||
        currently in Q with f(N') > f(N)
        ) {
      INSERT N' into Q or UPDATE N' within Q
    }
  } 
}

즉, 특이하게도 A* 목표 노드를 발견해도 종료하지 않습니다.
Goal state가 priority-queue에서 pop되었을 때만 종료하게 됩니다.

Modified Pathfinding

지금까지는 정적인 장애물만 피해갔지만, 이런 경우에는 어떡해야 할까요?

  • 동적인 장애물이 있을 경우
  • 이동 경로를 부드럽게 움직이게 하고 싶을 경우

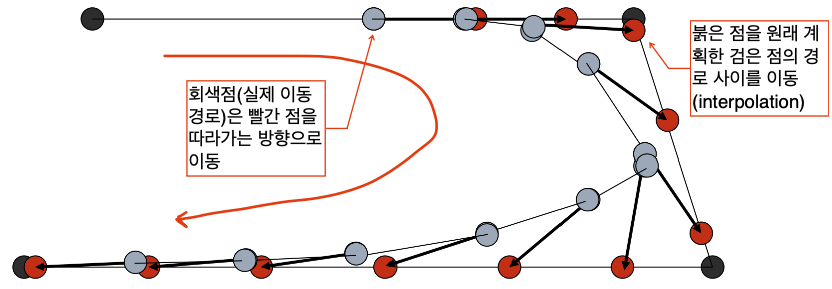
231211-221920

이동 경로를 부드럽게 하고싶은 경우에는 선형 보간을 사용하는 방식으로 해결할 수 있습니다.

동적인 장애물이 있는 경우에는 장애물이 움직인다고 A* 알고리즘을 다시 돌리는 행위는 너무 비효율적입니다.
따라서 A*에 약간의 Greedy 함이 추가되면 좋을 거 같습니다... 만, 어떻게 해야할까요?

Inadmissible

A*가 최적해를 구할 수 있는 조건은 휴리스탁한 길이 h가 실제 길이보다 같거나 짧아야한다는 admissible이 지켜졌기 때문입니다.
그렇다면 h가 inadmissible 하다면?

기존 휴리스틱 h에 α\alpha를 곱하여 inadmissible 하게 만들어봅시다.

h′(n)=α⋅h(n)h'(n) = \alpha \cdot h(n)

휴리스틱한 거리가 실제 거리보다 길어질만큼 α\alpha를 곱하여 inadmissible하게 만들었습니다.
하지만, 효율성을 챙길 수 있습니다.
왜냐하면, f가 동일하다고 했을 때, α\alpha를 곱한다면 f'의 값은 원래의 h가 작았던 경로가 더 작게 나올 것입니다.

즉, α\alpha값을 높임으로서 효율적인 탐색을 지향하지만, 그리디의 특성을 일부 챙길 수 있게 되었습니다.
(물론 이 과정에서 최적해는 구하지 못할 수 있습니다)

Hierarchical Planning

처음부터 전체적으로 세부적인 경로를 구하는 것이 아닌, 초기에는 듬성듬성한 탐색 경로를 설정하고, 나중에 세부적인 탐색 경로를 2차적으로 설정하는 방법입니다.

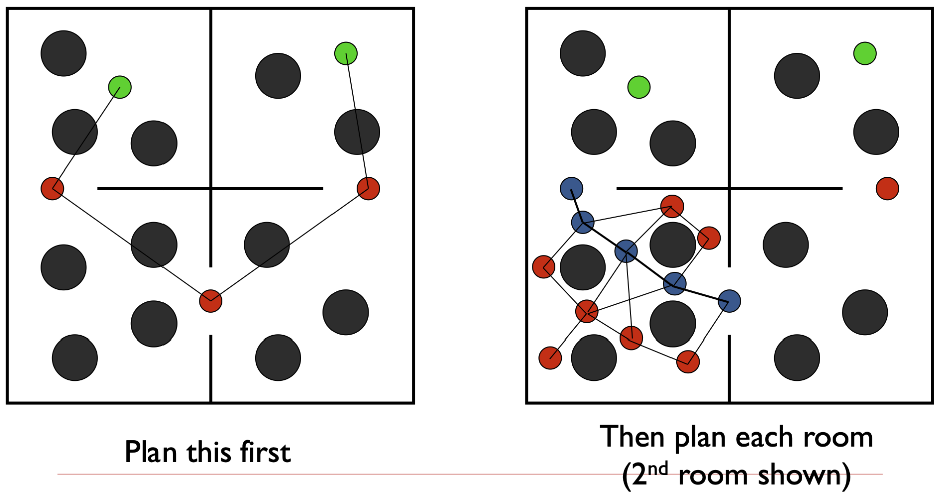
231211-221544

위에 소개된 두 방법은 일반적으로 비용이 저렴하며, 실제 필요한 영역만 탐색하기 때문에 효율적이고, 동적인 환경에 더 적응성이 강하다는 장점이 있습니다.
하지만, 최적해를 보장하지 못한다는 단점이 있습니다.

Dynamic Planning

전체 경로를 planning 하는 것이 아니라, 일부 경로만 planning하고, planning 한 경로의 끝에 다다를 때 쯤, 다음 경로를 planning 하는 방식입니다.

동적인 환경에 대한 적응성이 더욱 뛰어납니다.
하지만, 극단적인 경우에 한 스탭만 planning 하는 경우에는 그리디 방식과 동일해집니다.

Reactive Planning

위에서 언급한 Dynamic Planning의 극단적인 경우입니다.
즉, 최적성을 보장하지는 않지만, 빠르고, 자연스러운 움직임을 추구해야 하는 경우 사용하는 알고리즘 입니다.

Potential Field Planning

잠재적인 힘의 공간을 이용한 planning 방식입니다.
경로 탐색 공간을 두 가지 힘에 의해 좌우되는 공간으로 변형해봅시다.

F는 장애물에서 멀어지려는 힘을 가하는 공간이고, G는 목표지점으로 향하는 힘을 가하는 공간이라고 가정해봅시다.
이 떄, F+G인 공간에서 물리 시뮬레이션을 한다면?
매 순간마다 위치와 속도를 얻을 수 있고, 그 방향으로 움직인다면 자연스러운 선택을 유도할 수 있습니다.

231211-222259

하지만 문제가 많습니다.

  • 파라미터가 너무 많음
    힘, 가파르기, 속도, 질량 등 물리 시뮬레이션을 위한 파라미터가 너무 많이 필요합니다.

  • 목표의 충돌

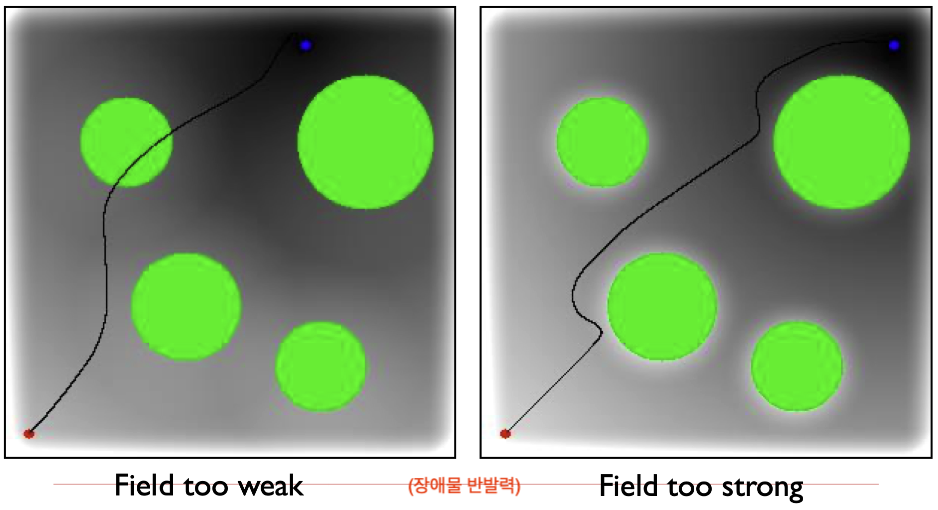
    231211-222520

    장애물을 피하려는 목표와 부드럽게 움직이려는 목표의 충돌로 부자연스러운 움직임을 보일 수 있습니다.

  • 국소 최적해

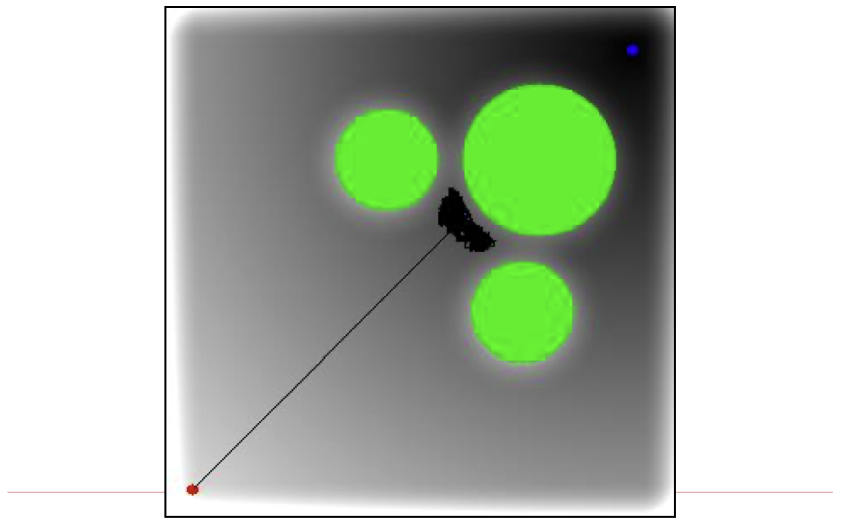
    231211-222543

    목적지로 이동하지 못하고 갇힐 수도 있습니다.

Flocking Models

경로를 파악해야 하는 객체, 즉 이동하는 객체가 집단일 경우에는 어떨까요?
집단 내부에서 규칙을 정해서 따르도록 하는 힘의 함수를 만드는 것이 도움이 됩니다.

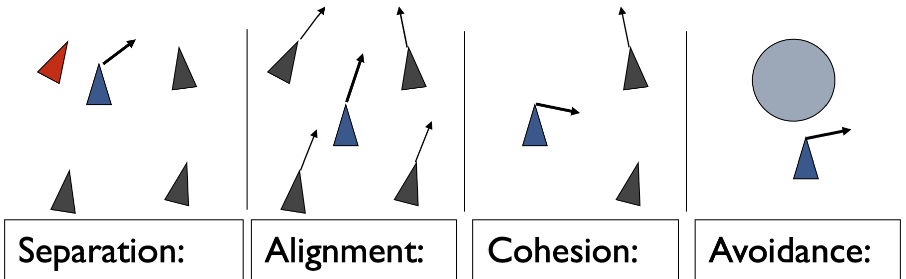
231211-222714

  • Separation
    일종의 personal space 개념으로 남들과 약간의 거리를 두고 싶은 정도의 힘 입니다.
  • Alignment
    남들과 같은 방향으로 같이 가려는 힘 입니다.
  • Cohesion
    집단에 속하려고 서로 응집하려는 힘 입니다.
  • Avoidance
    장애물을 회피하려는 방향으로 가려는 힘 입니다.

이런 4가지 힘의 행동 규칙에 가중치를 부여하여 집단의 이동을 결정하면 간단한 규칙들의 합으로 군중의 복잡한 움직임을 모방할 수 있습니다.
가중치를 부여하는 방식에 따라 우선순위가 낮은 규칙은 적용되지 않을 수도 있고, 모든 규칙이 고루 영향을 미치도록 할 수도 있습니다.

정리하자면, 복잡한 군중 행동을 단순하게 표현할 수 있고, 여러 행동양식을 만들어 낼 수 있다는 장점이 있지만,
가중치 조절이 쉽지 않으며, 앞서 봤던 Potential Field의 영향도 받을 수 있다는 단점이 있습니다.