Matrix and Transformations
행렬에 대한 기본적인 내용과 이를 이용한 공간상에서의 변환에 대해 다뤄봅니다.읽는데 11분 정도 걸려요.Matrix
m-by-n matrix, 또는 m행(Row) n열(Column) 의 행렬이라고 부른다.
여기서 하나의 행 만으로 이루어진 행렬을 Row vectors,
한 열로만 이루어진 행렬을 Column vectors 라고 부른다.
Transpose
각 행과 열을 뒤집은 행렬을 전치행렬 이라고 부른다.
Square Matrix
행과 열의 개수가 같은 행렬을 의미한다.
Identity Matrix
위와 같이 Square Matrix인데 대각선만 1이고, 나머지는 0으로 채워진 행렬을 의미한다.
AI = IA = A
이 행렬의 가장 큰 특징은 행렬 A에 Identity Matrix를 곱하면 다시 행렬 A가 나온다는 것이다.
Scalar Multiplication & Addition
백터에 스칼라 곱을 하거나, 백터간 합이나 차를 구할 때는 이전 포스트에서 벡터의 연산을 했을 때와 동일하게 각 원소에 대해 연산을 진행하면 된다.
Matrix Multiplication
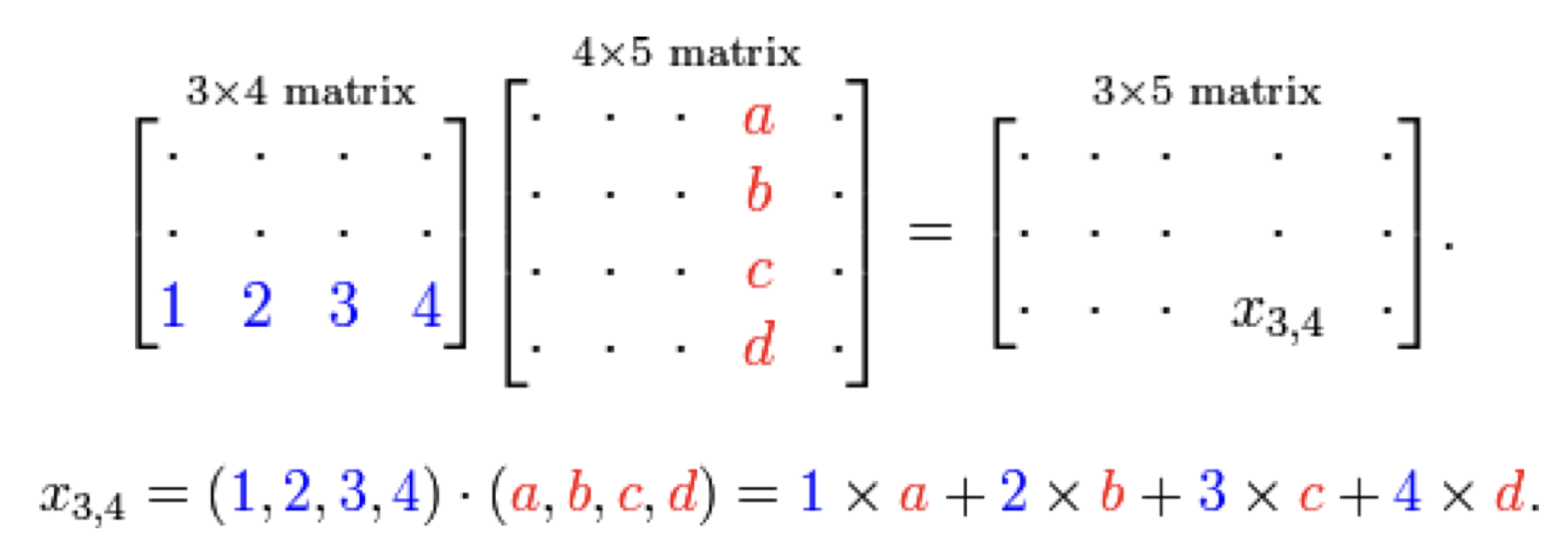
행렬간 곱 연산은 위의 이미지와 같이 계산된다.
여기서 주의할 점은 앞의 행렬의 열 의 개수와 뒤의 행렬의 행 의 개수가 일치해야 한다는 점이다.
Transformations
Basis
변환에 앞서 기저에 대해 알 필요가 있다.
선형 독립인 벡터들이 공간을 생성(span)할 때, 그 벡터의 집합을 기저(basis)라고 한다.
선형 독립 (Linear Independent)
N차원에서 어떤 하나의 벡터가 나머지 N-1개의 벡터의 선형 결합으로 표현할 수 없는 경우, N개의 벡터들이 선형 독립이라고 한다.
즉, 벡터간 의존성이 없어야 한다.
벡터가 공간을 생성한다는 의미를 잘 모를 수 있는데, 예로 들어보자.
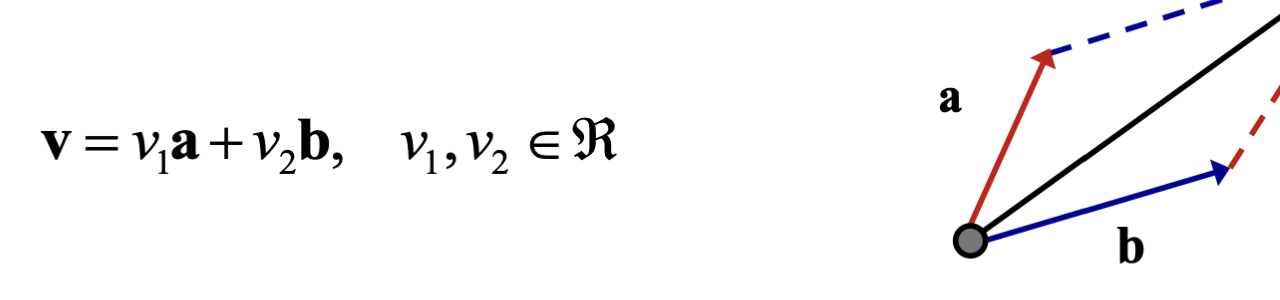
v는 한 평면위의 벡터이다.
이 상태에서 의 값을 [-, ] 범위로 임의 조정한다고 가정해보자.
그럼 v는 어떤 범위의 종점 좌표를 가질 수 있을까?
바로 벡터 a, b가 속한 평면의 모든 좌표를 가질 수 있을 것이다.
즉, 평행하지 않은 벡터의 선형 결합으로 공간을 생성할 수 있는 것이다.
그렇다면 두 벡터가 평행하지 않는다는 조건도 이해가 될 것이다.
만약 두 벡터가 평행하다, 즉, 하나의 벡터로 다른 벡터를 표현할 수 있다, 다른 말로 두 벡터가 선형 의존이라면, v는 직선상에만 존재할 수 있기 때문이다.
그럼 다시 basis 얘기로 돌아와서, basis의 선형 결합으로 basis가 span하는 공간의 모든 벡터를 표현할 수 있다는 것을 이해했다.
이 때 성립하는 증명이 있다.
같은 basis의 선형결합으로 표현되는 벡터는 표현 방법이 1개로 유일하다.
위의 증명된 내용 덕분에, basis의 선형 결합 시 사용하는 weight를 좌표로써 활용할 수 있는 것이다.
그렇기에 basis를 바꾼다는 건 좌표값을 바꾸는 것일 뿐, 벡터 그 자체를 바꾸는게 아니다.
Linear Map
선형 사상이란 벡터의 기저를 바꿀 때, 즉 벡터 공간이 바뀔 때 변형시에 선형성이 유지되는 변환 함수() 를 말한다.
예로 들어 아래는 선형 사상이다.
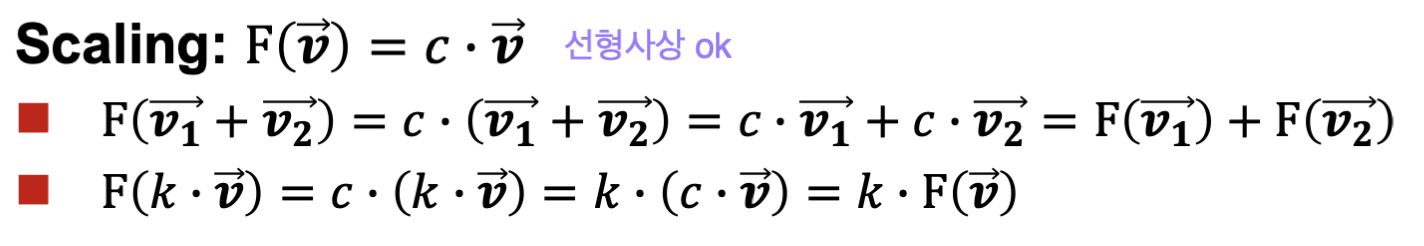
하지만, 이 경우는 선형 사상이 아니다.
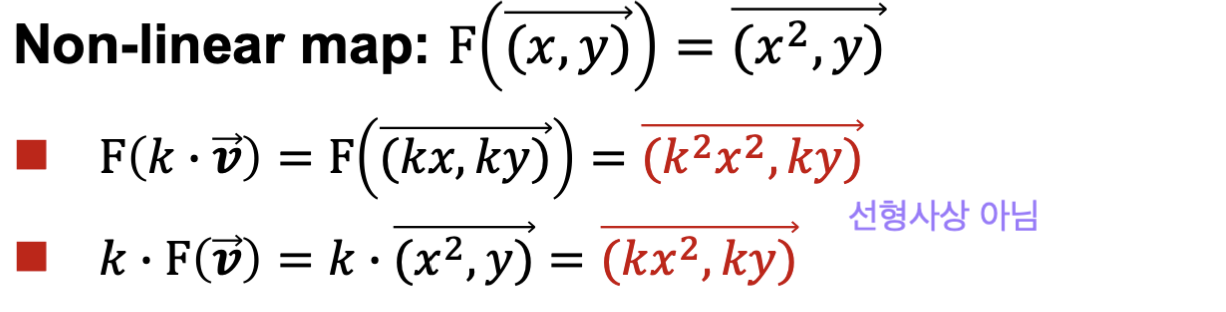
음? 그런데 이게 기저가 바뀌는거랑 무슨 상관이냐고?
이제 기저를 선형 사상(변환 함수)에 대입해보며 알아보자.
이해를 돕기 위해 , , 을 , , 라고 생각해보자.
이제 (, , ) 대신에 (1, 0, 0) 을 대입해보자.
이 때, (1, 0, 0)은 x축을 가리키는 기저의 원소이다.
즉, 선형 사상() 로 인해 기저 x(1, 0, 0)는 로 변환되었다.
여기서 알 수 있는 것은 선형 사상, Linear Function 의 i번째 열 벡터는 i번째 축의 기저벡터가 어디로 대응되는가를 알려준다.
또한, 위의 변환 과정은 선형성이 유지된다.
참고로 선형성이 유지되는 특성 덕분에 여러 선형 사상을 한 번에 처리하는 것 또한 가능해진다.
A(B(C(D(x)))) = ABCDx =
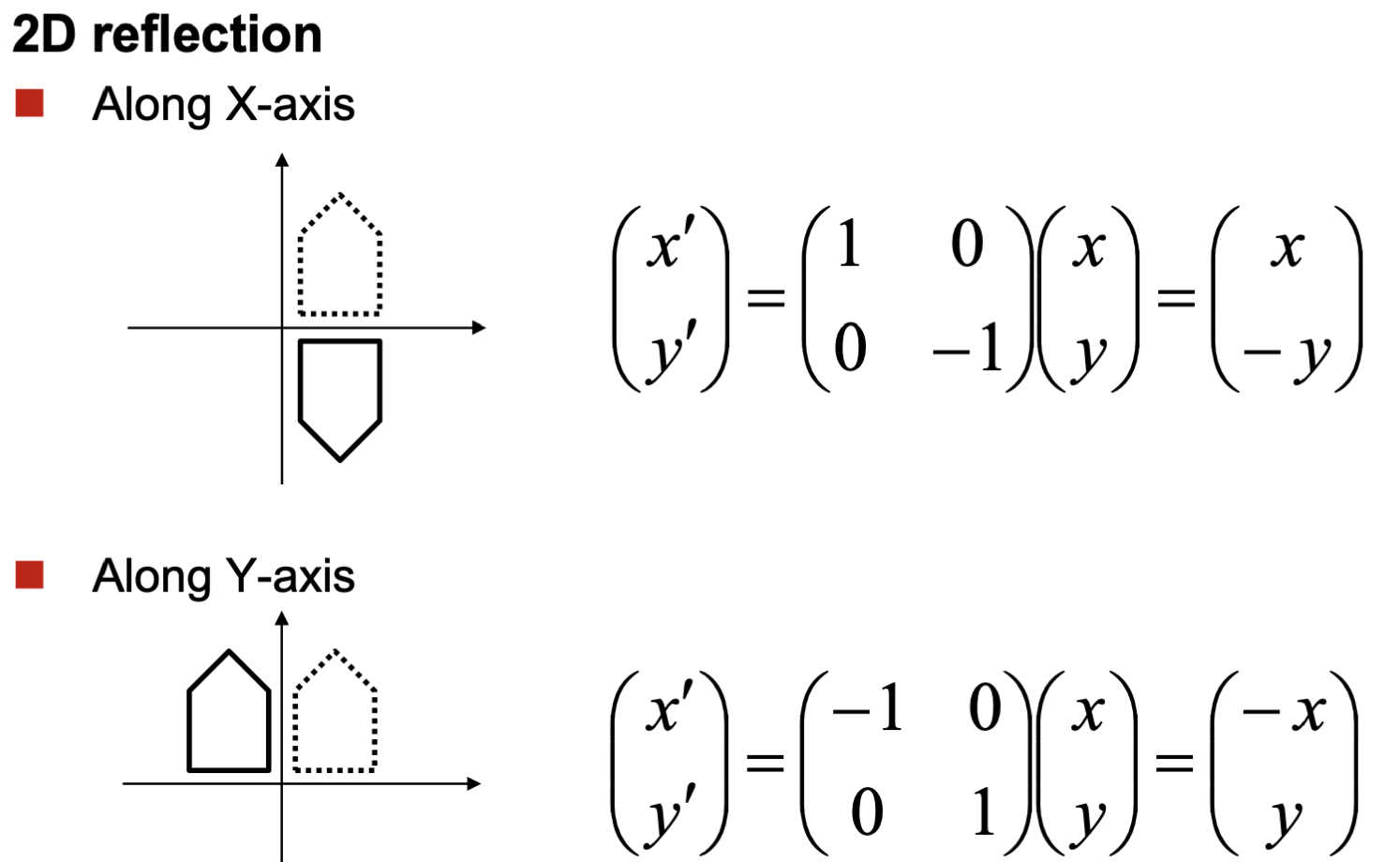
2D Linear Transformations
우선 회전을 살펴보자.
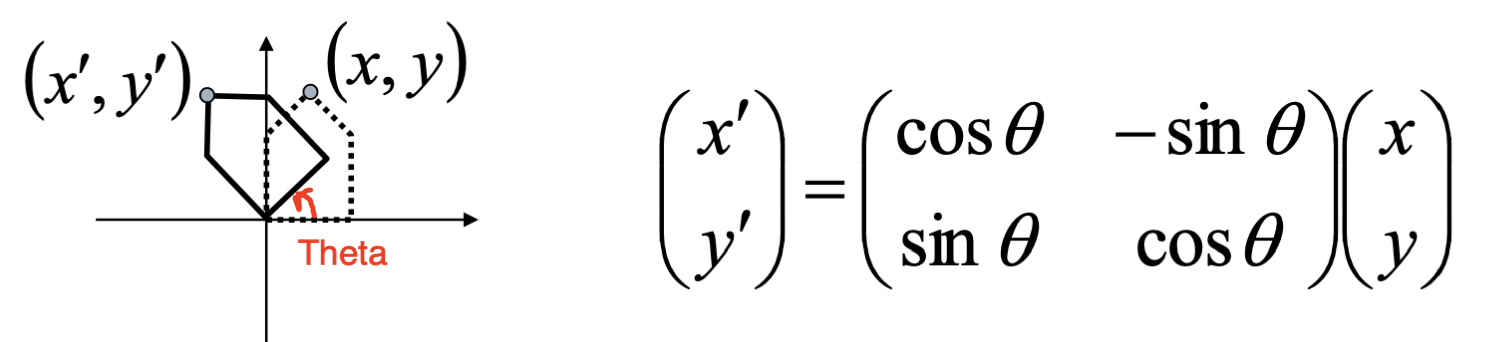
선형 사상을 이용한 기저의 변환을 어느정도 이해했다면 이제 변형식이 왜 이렇게 생겼는지도 이해할 수 있을 것이다.
예로 들어 (1,0) 즉 x축의 기저벡터를 만큼 회전시킨 좌표는 (, )가 되는데, 이는 위에서 언급한 "선형 사상, Linear Function 의 i번째 열 벡터는 i번째 축의 기저벡터가 어디로 대응되는가를 알려준다" 와 완벽히 일치한다.
즉, 앞으로의 변환은 각 축의 기저 벡터가 어떻게 변하는지를 파악하고, 해당 변화 후의 값을 이용해서 선형 사상 함수를 작성하면 된다.
이런 내용을 염두하고 다른 변환들도 살펴보자.
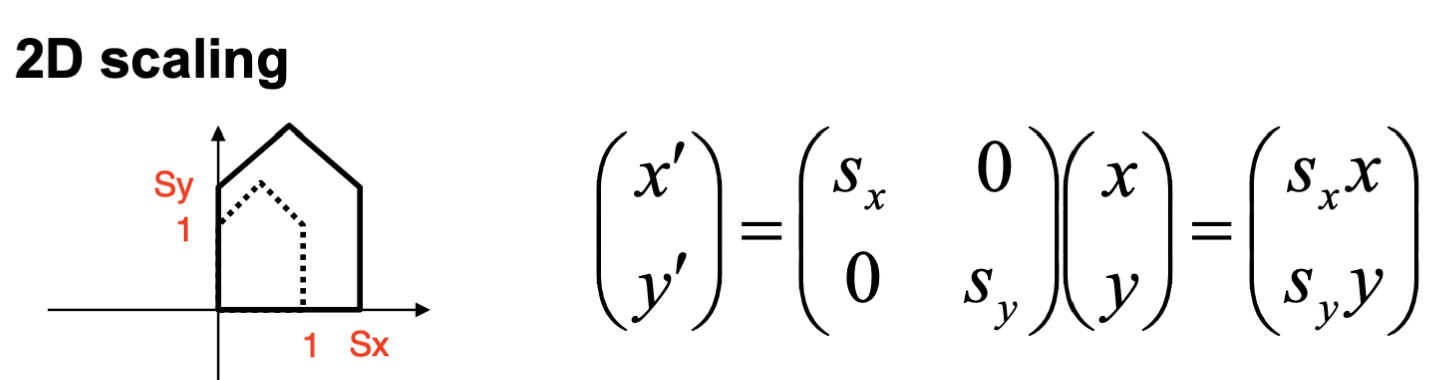
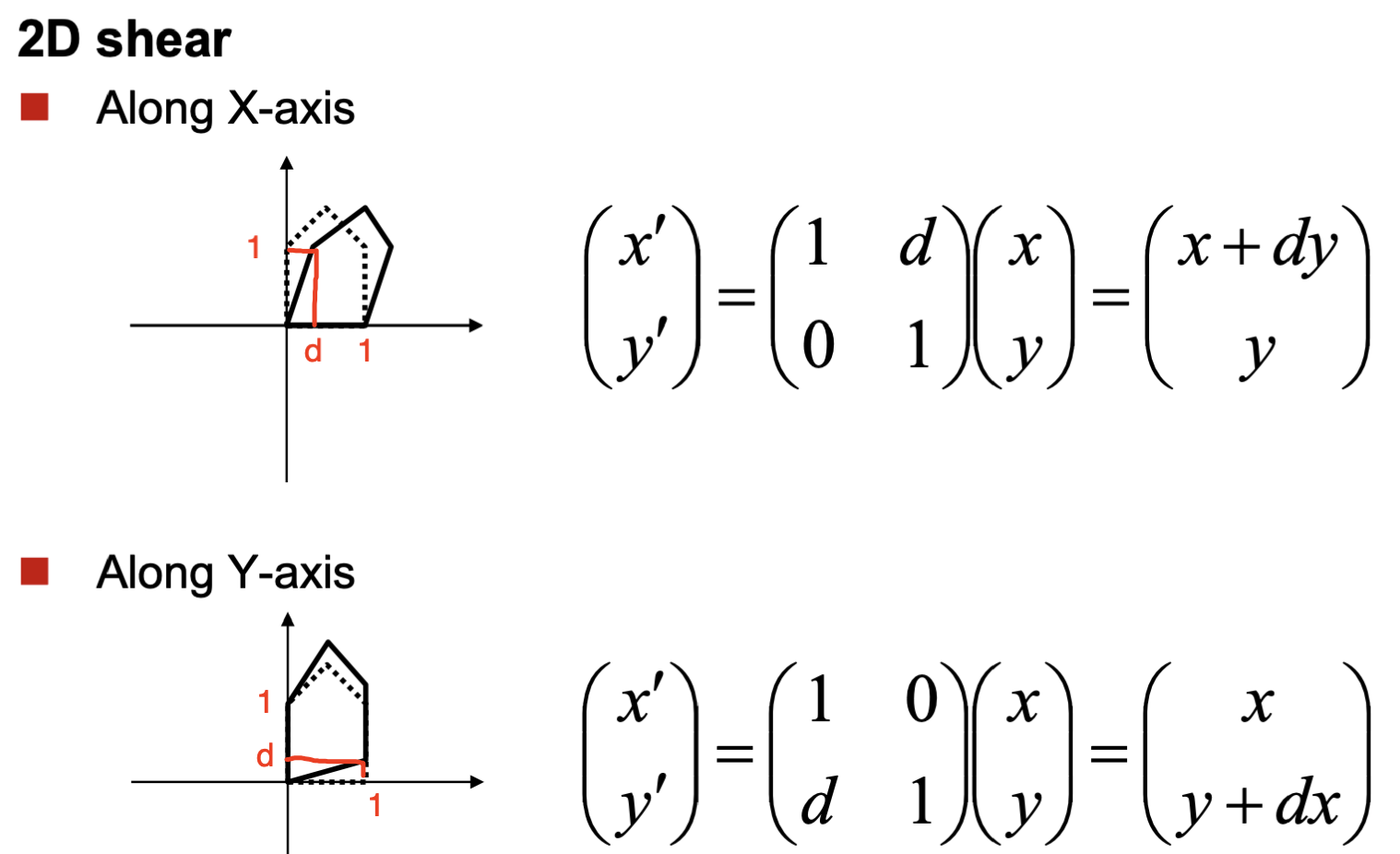
Affine Maps
2D Translation을 가능케하는 Transformations 이 있을까?
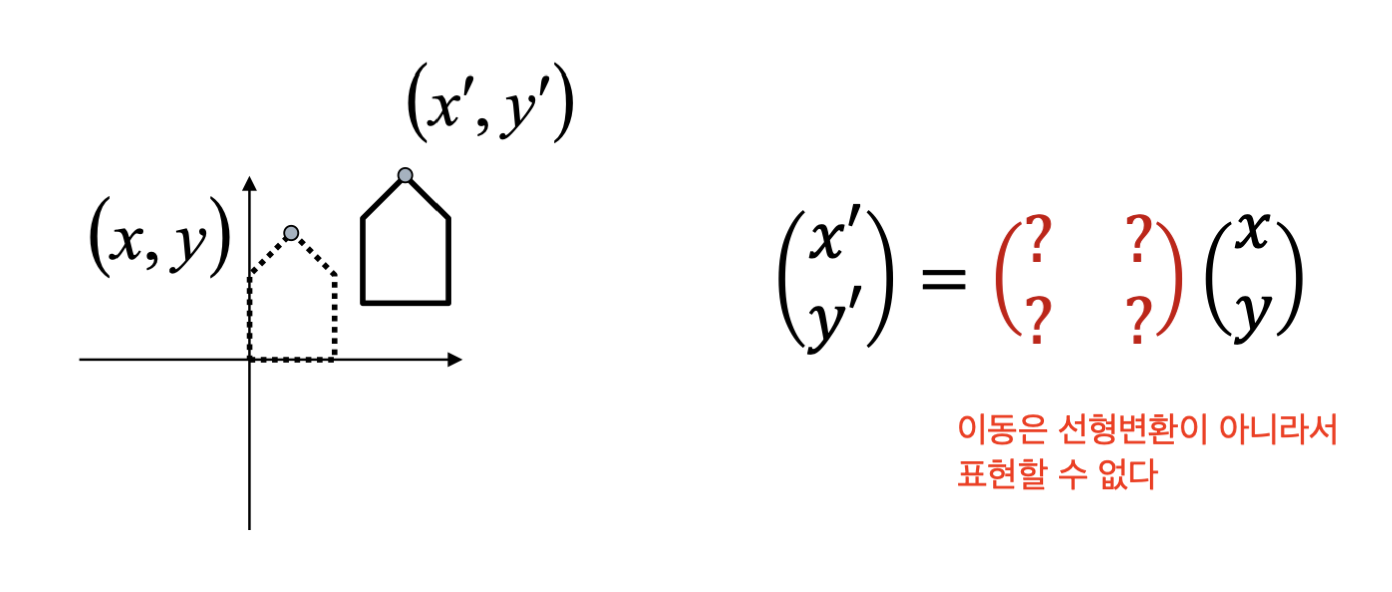
없다.
그 이유는 이동은 선형 변환이 아니라서 이를 표현할 선형 사상 함수가 없기 때문이다.
즉, Affine Map은 Linear map + Translation 으로 표현할 수 밖에 없다.
왜냐면 Affine은 Linear하지 않기 때문이다.
Homogeneous Coordinates
그렇다면 Transform과 Translate를 동시에 처리할 수 있는 방법이 없을까?
바로 Homogeneous Coordinates를 이용하면 된다.
이게 뭐냐면, 2차원의 Homogeneous Coordinates는 3차원의 벡터가 된다는 건데, 예시를 들어보자.
적당하게 w 기저를 하나 더 만들어서 차원을 높였다.
이 때, (, , )를 Homogeneous Coordinates 라고 하는데, 이제 여기에 계산의 편의를 위해 에 1을 대입해보자.
결과는?
놀랍게도 Transformations 한 방식과 동일하게 진행되었는데 결과는 Translate 한 결과가 나왔다.
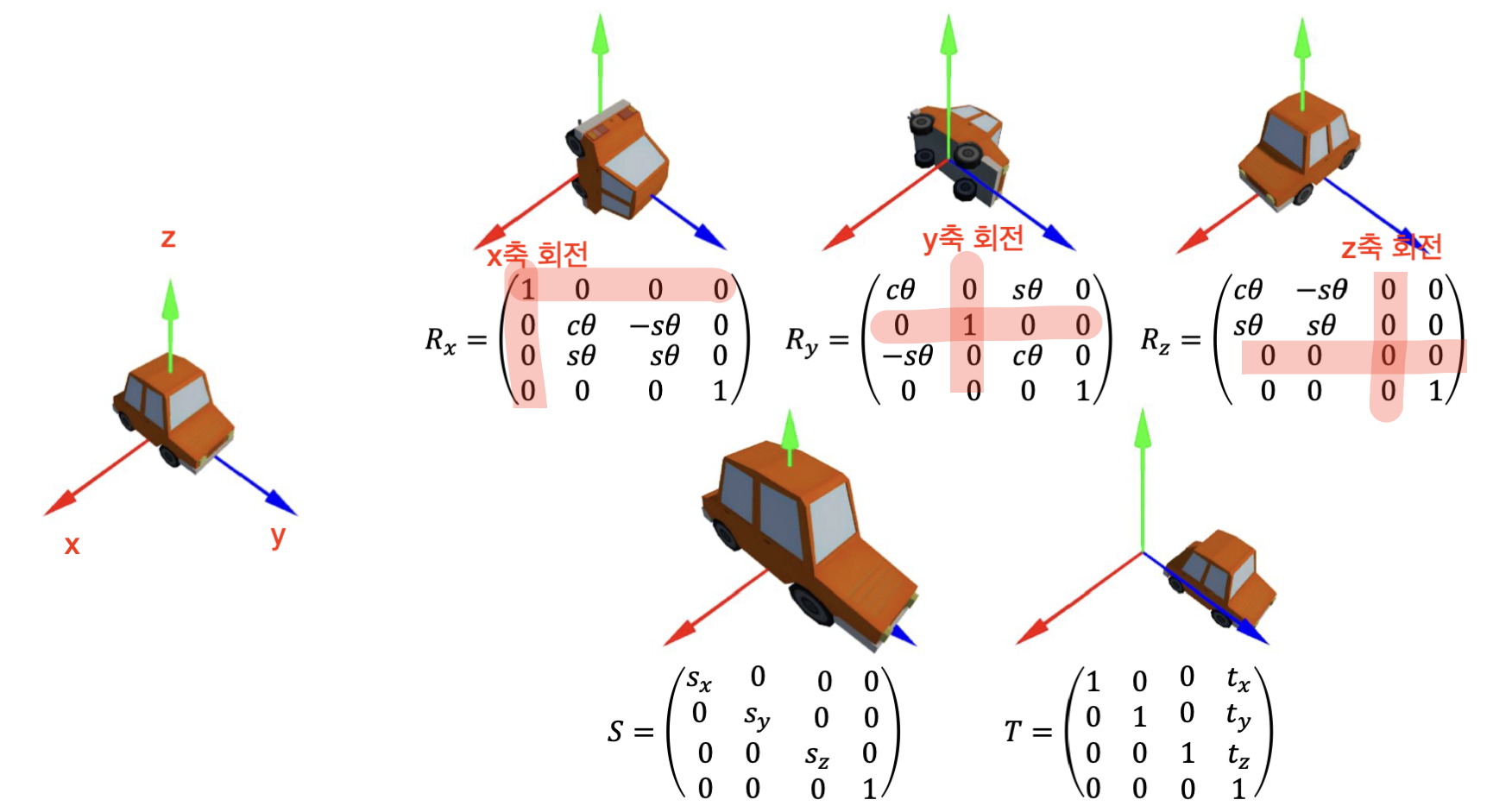
이를 이용하면 2D 에서의 모든 변형은 다음과 같은 4개의 행렬의 곱으로 표현이 가능해진다.

즉, 좌상단의 2x2 행렬은 Transform을 위한 부분이고, 우상단의 2x1 행렬은 Translate를 위한 부분이다.
참고용으로 3D에 대한 Homogeneous Coordinates도 남겨놓겠다.
Compound Transformations
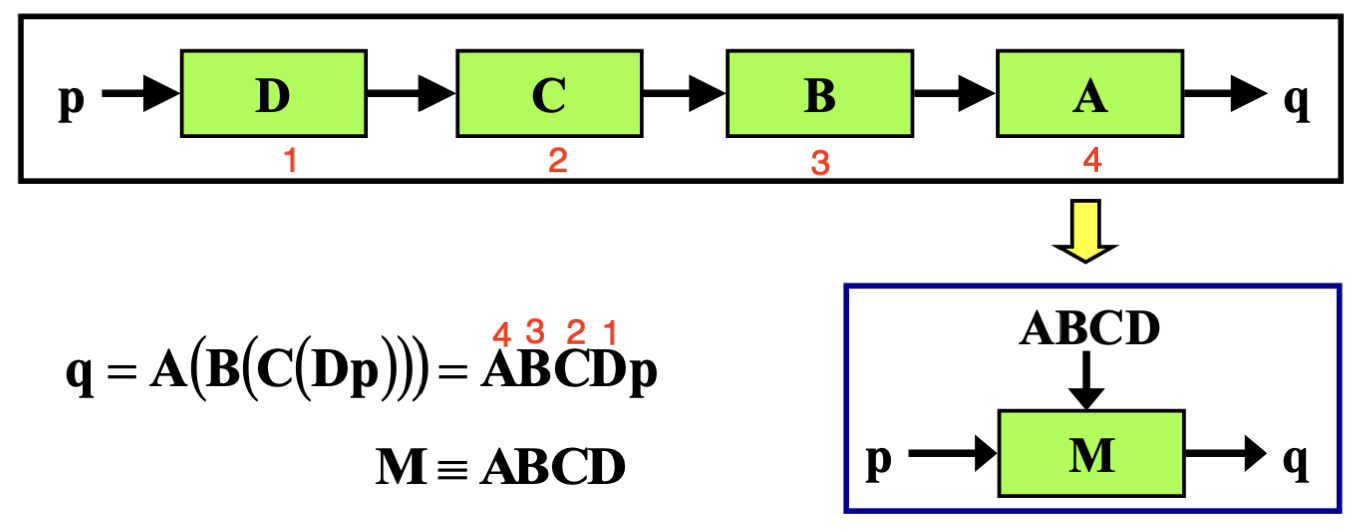
Linear Map의 마지막에 언급한 사실에 근거해 이제 모든 변환은 합성 변환으로 치환할 수 있다.
A(B(C(D(x)))) = ABCDx =
그렇게 하면 ABCDx 이 행렬곱을 정리하기만 하면 A~D 까지의 모든 변환을 한 번에 수행하는 결과를 얻을 수 있으니 연산량이 매우 감소하게 된다.
단, 연산 순서에 주의해야 한다.
이제 연산량이 어떻게 변하는지 예시를 살펴보자.

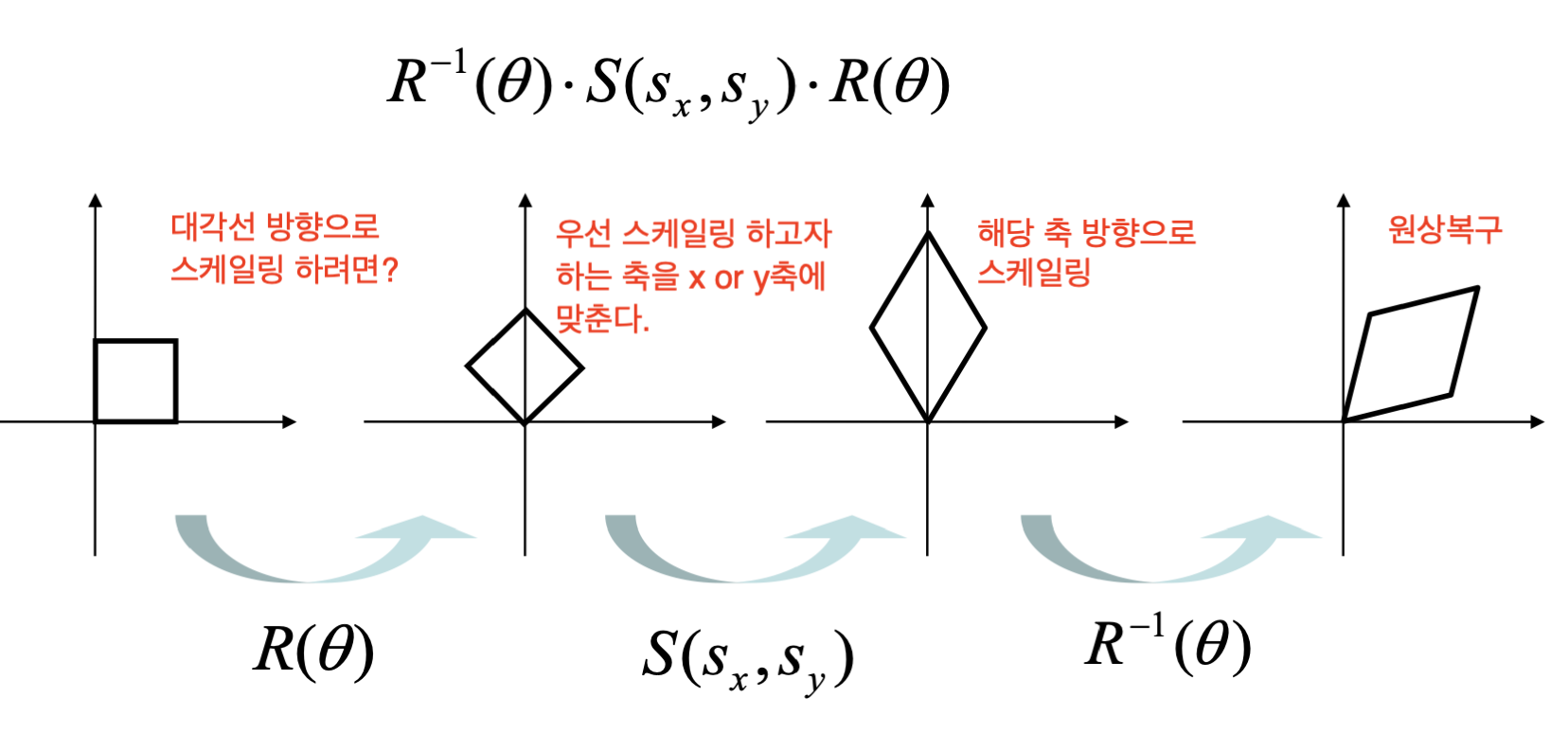
이를 응용하면 특정 방향으로만 스케일링 하는 것도 구현할 수 있다.