웅덩이

Kinematics

관절(Joints)와 뼈대(Links)의 트리구조의 계층적 모델로 표현 가능하며, 힘에 대한건 고려하지 않고, 관절의 각도만 고려하게 됩니다.

연산 순서에 따라 Forward, Inverse Kinematics로 구분되는데, 어떤식으로 다른지 알아봅시다.

Forward

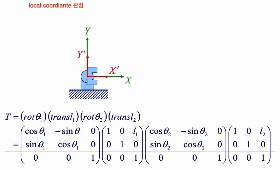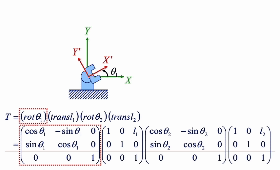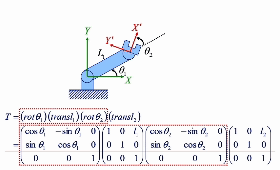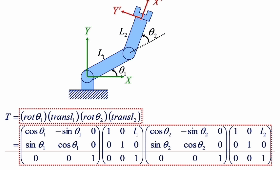
local coordinate 관점
Inverse

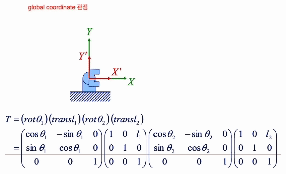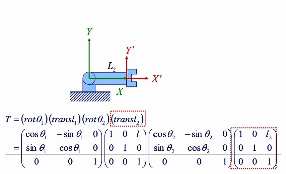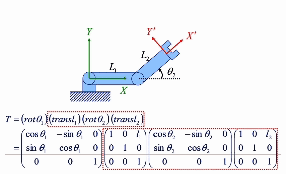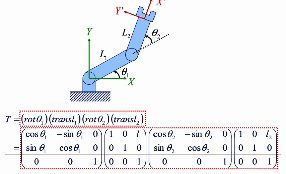
global coordinate 관점

사실상 동일합니다.

3차원의 경우 회전은 각 축을 중심으로 하는 3개의 회전으로 분리(Eular angles)하여 계산합니다.

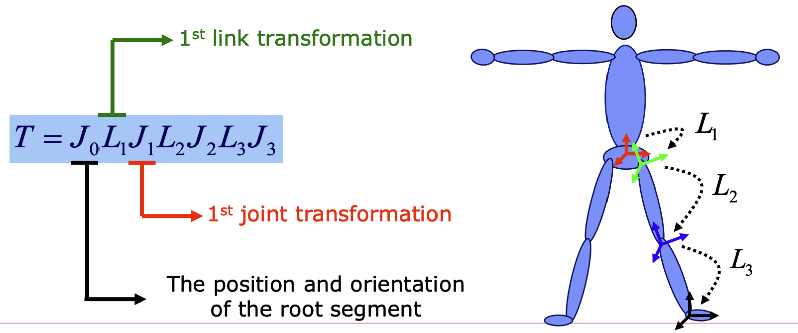
231211-180643

각 관절과 뼈대는 트리구조로 표현된다고 했었는데, 각 관절의 회전과 뼈대의 길이를 DFS 방식으로 탐색하며 계산한다면 원하는 부분의 움직임을 계산할 수 있습니다.

Rotation

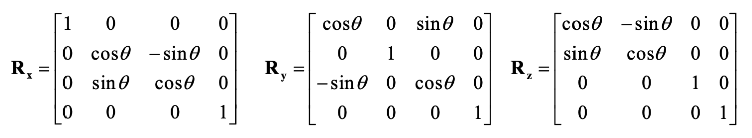
231211-180857

지금까지 3차원에서의 회전은 Eular angles를 연산하여 계산했었습니다.
하지만, 이 방식에는 치명적인 단점이 존재합니다.

연산 순서에 따라 결과가 달라진다.
Gimbal lock 현상이 발생한다.

Gimbal lock

가장 안쪽에 있는 축(Gimbal)과 가장 밖에있는 축이 평행하게 되어버리면 회전의 자유도의 손실이 발생하는 현상.
예시 영상

따라서 이를 해결할 두 가지 3차원 회전방법을 알아보겠습니다.

Quaternion

4개의 파라미터로 4차원 공간의 구의 좌표(4원수)를 사용합니다.

q = (w, x, y, z) \\ {}\\ w^2 + x^2 + y^2 + z^2 = 1

쿼터니언은 복소수의 확장판으로 엄밀한 정의는 다음과 같습니다.

w + ix + jy + kz = (w,x,y,z) = (w,v) \\ {}\\ i^2 = j^2 = k^2 = ijk = -1

231211-183507

즉, 교환법칙이 성립되지 않으며, 허수부의 연산을 표로 그려보면 다음과 같습니다.

x	1	i	j	k
1	1	i	j	k
i	i	-1	k	-j
j	j	-k	-1	i
k	k	j	-i	-1

이제 쿼터니언의 여러 연산을 알아봅시다.

Add, Sub
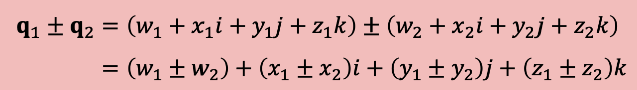
Mul
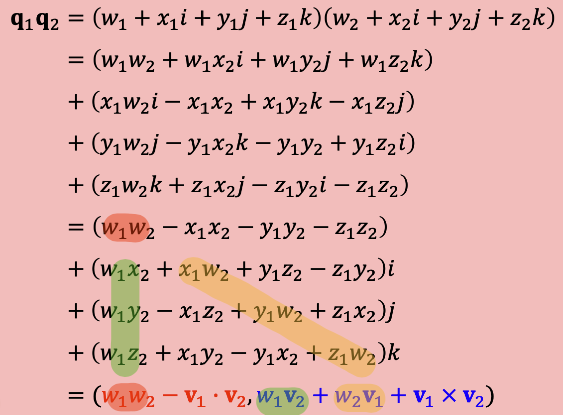
Conjugate (켤레 복소수)
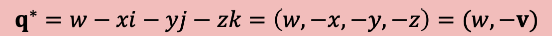
Norm (크기)
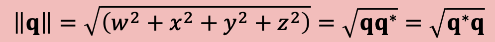
Mul Identity (곱셈 항등원)
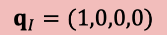
Mul Inverse (곱셈 항등원의 역)

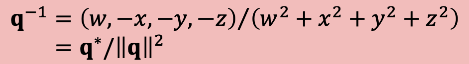
근데 쿼터니언이 왜 회전과 관련이 있는걸까요?
다음을 보며 이해해봅시다.

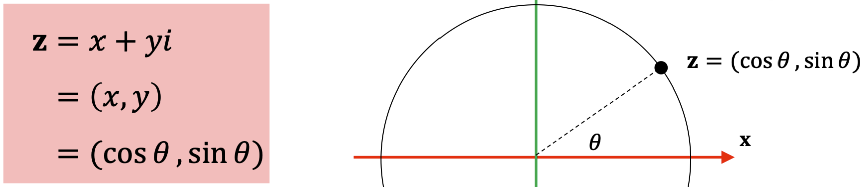
231211-185645

오일러 공식에 의한 회전은 가장 아름다운 수식으로 알려진 만큼 유명해서 익숙할 겁니다.

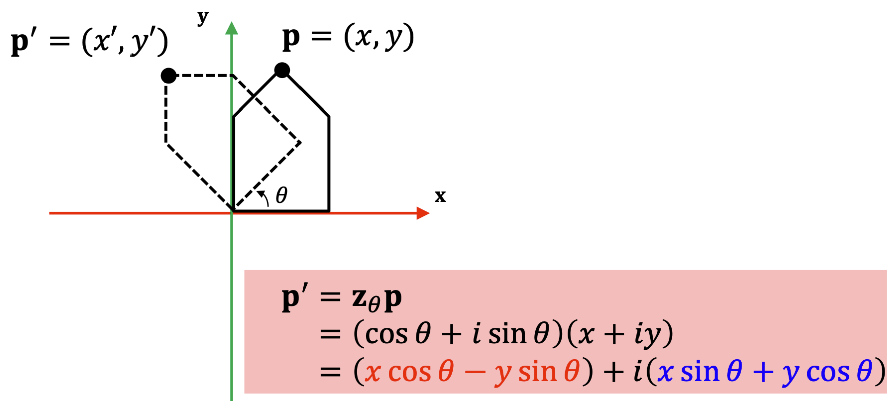
231211-185900

실제로 전에 다뤄본대로 변환 행렬의 원소가 실수부와 허수부의 변환된 좌표로 나오게 됩니다.

231211-190100

위 개념을 확장하면 쿼터니언을 사용하면 3차원의 회전을 다룰 수 있다는 사실을 알 수 있습니다.

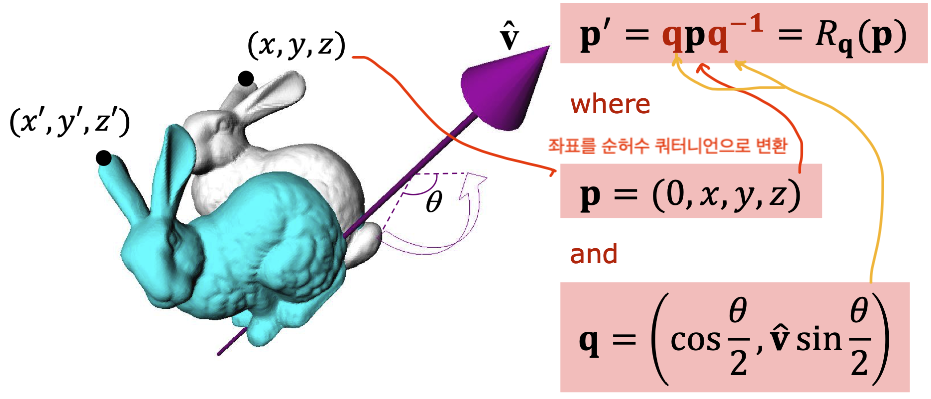
231211-190242

즉, 회전하고자 하는 좌표를 순허수 쿼터니언으로 변환하고,
특정 축(유닛 벡터)을 기준으로 회전각을 곱해주면 회전된 좌표가 순허수 쿼터니언의 형태로 나오게 됩니다.

Rotation Matrix

9개의 파라미터로 3차원 회전을 달성하는 3by3 행렬입니다.

R = \begin{bmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3 & v_3 & w_3 \\ \end{bmatrix} = \begin{bmatrix} u & v & w \\ \end{bmatrix}

여기서 u, v, w는 단위벡터이고, det(R) = 1 인 회전 행렬입니다.

파라미터가 9개나 되는데 굳이 rotation matrix를 사용하는 이유는 무엇일까요?
쿼터니언은 부호가 반대가 되는 경우가 있기 때문입니다.

R_q(p) = R_{-q}(p)

즉, 하나의 회전을 2개의 방법으로 표현할 수 있기 때문입니다.
반면에 rotation matrix는 하나의 회전이 유니크한 matrix 하나로 정의되기에 사용합니다.

물론, 쿼터니언-회전행렬간 변환 연산도 있습니다.

Splines

애니메이션의 움직임을 부드럽게 하려면 어떻게 해야할까요?
수학적인 함수를 사용해서 시간 분할(간격)에 관계없이 애니메이션(위치)를 얻거나, 아주 잘게 쪼갠 미리 계산된 값(위치)를 사용하는 방법이 있을 것입니다.

다항식으로 이루어진 curve를 polynomial curve 라고 하는데 단순히 다항식을 사용하면 문제가 있습니다.
특정 점(위치)를 지나는 다항식을 계산하기가 어렵고, 차수가 높아질수록 불가능에 가까워집니다.

따라서 다음과 같은 방식을 사용해볼 수 있겠습니다.

Lagrange Polynomial

라그랑주 다항식은 아래와 같이 생겼습니다.

x(t) = L_0(t)x_0 + L_1(t)x_1 + ... + L_n(t)x_n \\ {}\\ L_k(t_i) = \left\{\begin{matrix} 1 \; if \; k=i \\ 0 \; if \; k \neq i \end{matrix}\right.

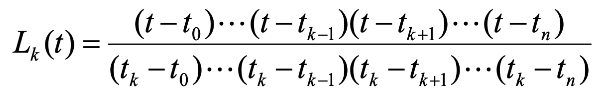
231211-201931

즉, $x(t_0) = x_0$ , $x(t_1) = x_1$ 과 같이 값이 나오기 때문에 원하는 함수 모양을 잡기 쉽습니다.
그러나, 차수가 높아질수록 L이 출렁이는, 일명 Oscillation 현상이 발생하기 때문에 keyframe particle motion에 적용하기에는 부적절합니다.

Spline Interpolation

그렇다면 아래와 같이 해결해볼 수 있을 거 같습니다.

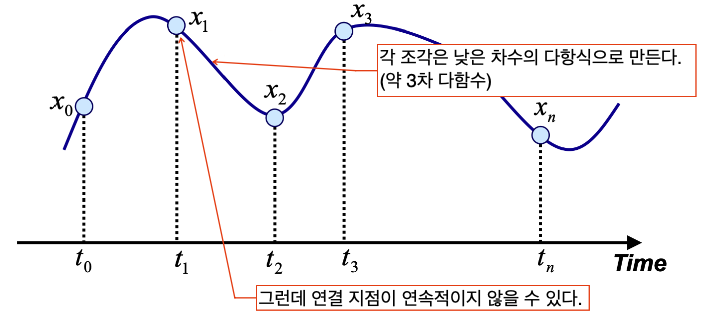
231211-202159

여기서 3차를 사용하는 이유는 2차는 평면상의 곡선만 표현할 수 있기에 공간의 움직임을 표현하기에는 부적절하고, 4차는 Oscillation 현상이 발생하기 때문에 부적절하기 때문입니다.
하지만 이 역시 문제가 있습니다.

우선 연걸지점이 미분 불가능할 수 있기에 움직임이 부자연스러울 수 있습니다.
또한, 일반적인 다항함수의 기저( $t^3$ ~ $t^0$ )로는 직관적으로 다항식이 어떤 모양인지 알 수 없습니다.

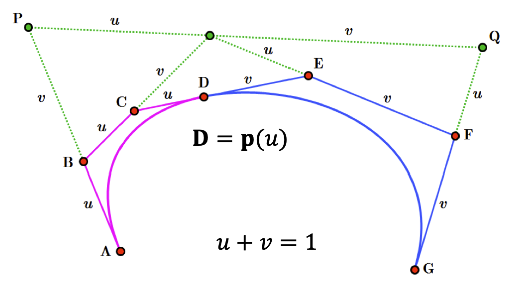
Bezier Curve

우선 기저만 봤을 때 함수의 모양을 직관적으로 확인할 수 있도록 Bernstein 기저 함수를 사용할 수 있겠습니다.

B_i^n = (_nC_i)(1-t)^{n-i}t^i

Bernstein 기저 함수의 특징은 아래와 같습니다.

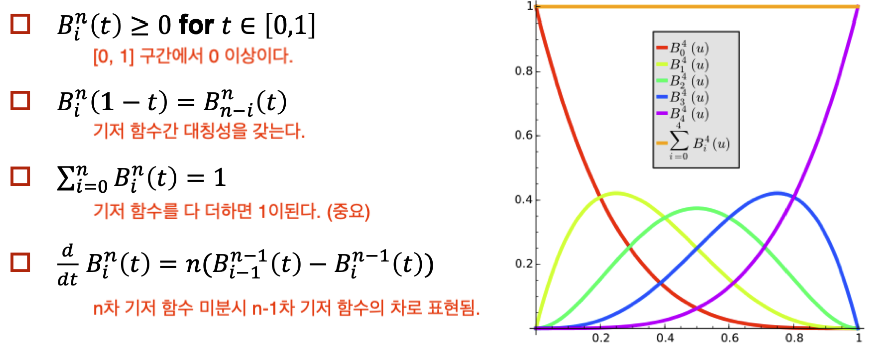
231211-203158

이 기저를 이용한 3차 다항식은 아래와 같습니다.

p(t) = B_0^3(t)b_0 + B_1^3(t)b_1 + B_2^3(t)b_2 + B_3^3(t)b_3 \\ {}\\ = (1-t)^3b_0 + 3t(1-t)^2b_1 + 3t^2(1-t)b_2 + t^3b_3

여기서 b의 값을 알면 함수의 모양을 예측할 수 있는데, 함수 p가 Bezier curve 입니다.

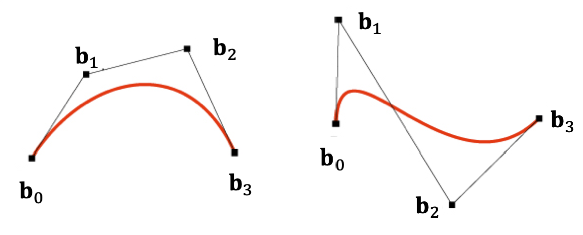
231211-203320

이 때의 $b_i$ 를 control point라고 부릅니다.

베지어 곡선의 특징은 다음과 같습니다.

End point interpolation

항상 $p(0) = b_0$ , $p(1) = b_3$ 입니다.
즉, 시점과 종점을 바로 알 수 있습니다.
Convex hull

항상 control points가 만드는 가장 작은 다각형(볼록한 모양) 내부에 베지어 곡선이 위치합니다.

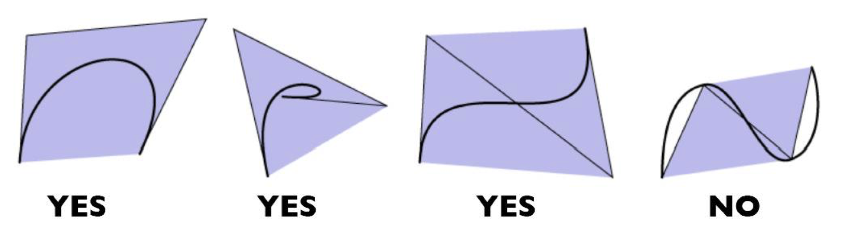
이 특성은 곡선이 교차되는 지점을 구할 때, 계산 범위를 한정지어 효과적으로 계산할 수 있도록 도와줍니다.
Affine inveriance

동일한 control points는 반드시 1개의 베지어 곡선만 생성합니다.
즉, control points를 transform 하는 경우에는 동일한 transform이 베지어 곡선에 적용되는 효과를 갖습니다.
Tangent vectors

시점, 종점의 탄젠트 벡터는 각 시/종점과 인접한 control point의 차이의 3배로 표현됩니다.

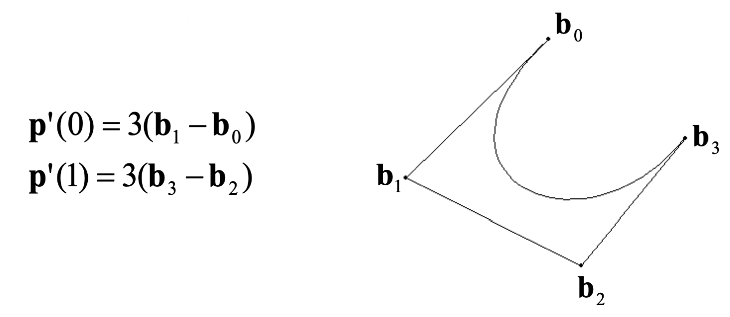
여기서 Spline Interpolation의 또 다른 문제였던 연결지점이 부자연스러울 경우를 예방할 수 있겠죠?

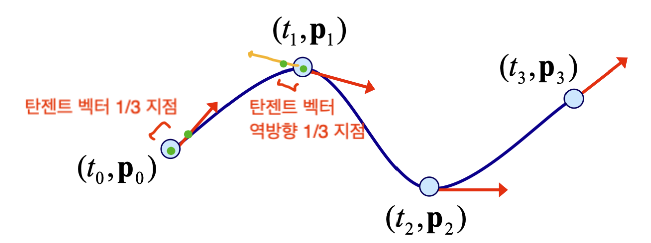
끝 점의 탄젠트 벡터의 방향을 일치하도록 설정하면 됩니다.
다르게 표현하면, 각 곡선 조각의 끝에 탄젠트 벡터가 있다면, 이를 이용해서 조각에 해당하는 베지어 커브를 그릴 수 있습니다.
Subdivision

베지어 곡선위의 임의의 점으로 곡선을 분할하면 분할된 곡선 역시 베지어 곡선이 됩니다.
De Casteljau's algorithm

시점 $t_k=u$ 일 때의 위치는 u:1-u로 내분하는 방식으로 구할 수 있습니다.