🫧

Clustering

여러 군집화 방법에 대해 알아봅니다.읽는데 17분 정도 걸려요.

Clustering

군집화란 여러개의 점(데이터)들의 집합이 주어졌을 때, 거리에 따라 점들을 그룹으로 묶는 행위를 의미합니다.
점들을 그룹으로 묶을 때는 유사도(거리)를 기준으로 cluster를 생성하게 되는데요, 사용되는 거리의 단위에는 아래와 같은 것들이 있습니다.

  • Euclidean

    • L2L_2 norm
      일반적인 두 점 사이의 거리 ((xa−xb)2+(ya−yb)2\sqrt{(x_a - x_b)^2 + (y_a - y_b)^2})

    • L1L_1 norm (Manhattan distance)
      차원별로 두 점 사이의 거리 (∣xa−xb∣+∣ya−yb∣|x_a - x_b| + |y_a - y_b|)

    즉, L1, L2 norm이 같은 경우는 같은 차원 축 위에 존재하는 경우밖에 없습니다. (L1의 값이 L2보다 같거나 더 큽니다)

    L2는 차원간 거리의 차이가 클 수록 페널티를 부여하는 효과가 있습니다.


    예로 들어, 점 x로 부터의 거리가 각 축별로 다음과 같다고 가정해봅시다.
    A = 2,3,4
    B = 1,3,5


    이 때 L1는 거리가 9로 같지만, L2는 B가 더 멀다고 판단합니다.
    (3축의 거리차가 더 크기에 더 큰 페널티 부여)

  • Cosine (for vector)
    cos(x,y)=x⋅y∣∣x∣∣⋅∣∣y∣∣cos(x,y) = \frac{x \cdot y}{||x|| \cdot ||y||}
    방향성이 얼마나 비슷한지를 거리로 사용합니다.
    내적 식과 동일합니다.

  • Jaccard (for sets)
    e.g. Jaccard 유사도가 1이다 → 두 원소가 완전 일치한다 → 거리는 0이다

  • Edit distance (for strings)
    문자열 x가 문자열 y로 변환되기 위한 과정의 횟수를 거리로 사용합니다.
    여기서 LCS 라는 개념이 등장하는데, LCS는 끊겨도 상관없는 올바른 순서로 존재하는 공통 문자 쌍의 개수를 의미합니다.
    e.g. x = abcde, y = bcduve → LCS(x, y) = bcde
    |x| - |y| - 2|LCS(x, y)| = 5 + 6 - 2*4 = 3 → distance = 3

    x = ab, y = ba의 경우에는 LCS가 a or b 로 2개 생길 수도 있습니다.
    이 경우의 x, y의 edit distance는 아무튼 2로 동일하긴 합니다.

단, 클러스터링을 하더라도, 특정 클러스터가 어떤 그룹인지는 알 수 없습니다.
사람이 직접 라벨링을 하거나, 데이터의 분포로 추측하는 수 밖에 없습니다.

Curse of Dimensionality

그럼 단순하게 거리계산을 이용한 클러스터링? 쉬워 보입니다.
하지만 현실은 차원의 저주 때문에 클러스터링이 제대로 이뤄지지 않습니다.

차원의 저주란 고차원에서 보면 매우 달라보이는 두 데이터가 비슷하게 분류되는 문제를 의미합니다.
예시와 함께 알아봅시다.

구간 [0, 1] 사이에 1만개의 서로 다른 점이 있다고 가정해봅시다.
0.1%, 즉 10개의 이웃한 점을 추출한다고 했을 때 각 차원별로 축의 몇%에 해당하는 범위의 점들이 포함될까요?

1차원에서는 일직선 위의 0.1%, 즉, 축위의 0~0.001 사이의 점들이 비슷한 정도 0.1%에 해당하는 점들입니다.
2차원에서는 평면위의 0.1%, 즉, 각 축위의 0~0.032 사이의 점들이 비슷한 정도 0.1%에 해당하는 점들입니다. (0.0322≈{^2} \approx 0.001)
n차원에서는 n차원의 0.1%, 즉, 각 축위의 0~0.0011/n^{1/n} 사이의 점들이 비슷한 정도 0.1%에 해당하는 점들입니다. ((0.0011/n^{1/n})n{^n} = 0.001)

즉, 차원이 높아질수록 각 축에서는 더 넓은 범위에서 비슷하다고 판단하게 됩니다.
10차원(n=10)의 경우에는 (0, 0, ... , 0)과 (0.5, 0.5, ..., 0.5)도 상위 0.1%로 비슷하다고 판단해 버립니다.

Clustrting Strategies

클러스터링 전략은 크게 2가지로 나뉩니다.

  1. 계층적 클러스터링

    1. bottom up
      각 점이 클러스터 1개를 생성사고, 가까운(비슷한) 클러스터끼리 병합하여 커지는 방식
    2. top down
      하나의 단일 클러스터로 시작하여 클러스터를 분리해나가는 방식

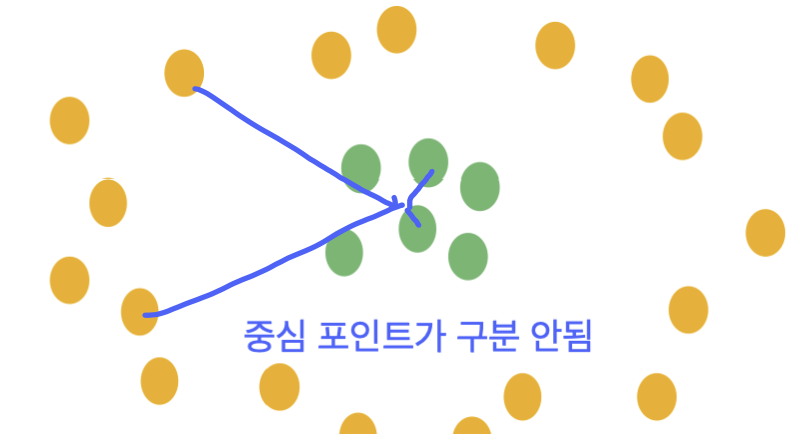
    231203-230112

    중심 포인트가 구분되지 않는다면 hierachical 방식이 더 좋습니다.

  2. 점 할당 클러스터링

    하나의 점을 향하는 점들끼리 클러스터링 하는 방식 (e.g. k-means)

    231203-230031

    중심 포인트가 구분된다면 point-assignment 방식이 더 좋습니다.

또한, 데이터가 유클리드 공간에 표현할 수 있는 경우에는 거리를 L1, L2 norm과 같은 유클리드 거리로 계산하지만,
유클리드 공간에 표현 불가능한 경우에는 거리를 Cosine, Jaccard, Edit-distance 등으로 거리를 계산합니다.

Hierachical Clustering

계층적 클러스터링 중에서 bottom-up 방식의 클러스터링에 대해 알아보겠습니다.
이 경우에는 클러스터링을 할 때, 다음과 같은 의문점을 해결해야 합니다.

  1. 클러스터를 어떤식으로 표현하는가?
  2. 가까운(비슷한) 클러스터의 기준이 무엇인가?
  3. 합치는 과정을 언제 멈추는게 좋은가?

이 경우에는 유클리드 공간과 비 유클리드 공간에서 정의되는 경우를 나누어서 살펴보겠습니다.

In Euclidean

1에 대한 해결방법으로 centroid 개념을 도입하면 됩니다.
Centroid란, 클러스터 내부 점들의 평균값으로 가상의 점을 생성하여 그 가상의 점을 centroid라고 합니다.

2에 대한 해결방법으로, 유클리드 공간의 경우 centroid간 거리가 가장 짧은 클러스터가 가장 가까운 클러스터가 됩니다.
즉, centroid가 가장 짧은 두 클러스터를 병합하면 됩니다.

3에 대한 해결방법으로, 아래와 같은 경우에 병합을 중단하는게 좋습니다.

  • 클러스터의 직경이 너무 커질 경우
  • 클러스터의 밀도가 너무 작을 경우
  • 클러스터의 직경이나 밀도의 변화가 급작스럽게 변할 경우

중단에 대한 평가법은 비 유클리드 공간에서도 동일하게 사용되기 때문에 비 유클리드 공간에서는 굳이 2번 언급하지 않겠습니다.

In Non-Euclidean

비 유클리드 공간에서는 centroid를 정의할 수 없습니다.
따라서 이를 대신할 방법이 2가지 정도가 존재합니다.

  • A - clusteroid
  • B - 클러스터 내부의 모든 점으로 표현

따라서 여기서 또 케이스를 나누어 살펴봅시다.

1-A에 대한 해결방법으로 clusteroid 개념을 도입합니다.
가상의 점인 centroid와 다르게 clusteroid는 실제로 존재하는 포인트 중 하나를 대표값으로 설정하는 방법입니다.
따라서 점들 중에서 어떤 점을 clusteroid로서 선택할지에 대한 여러 방법론이 존재합니다.

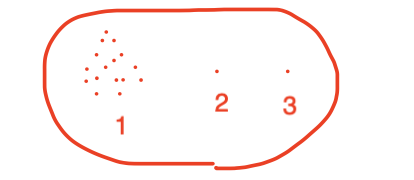
231204-123642

클러스터의 내부 점들이 아래와 같이 형성되었다고 가정해봅시다. (2, 3번은 outlier)

  1. inf-norm

    다른 점들까지의 거리의 최댓값이 가장 작은 점을 선택하는 방법입니다.
    이 경우에는 2의 점이 clusteroid로 선택이 될 것입니다.

  2. L1-norm

    다른 점들까지의 평균 거리가 가장 짧은 점을 선택하는 방법입니다.
    이 경우에는 1에 있는 점들 중 하나가 clusteroid로 선택이 될 것입니다.

  3. L2-norm

    다른 점들까지의 거리 제곱의 평균이 가장 짧은 점을 선택하는 방법입니다.
    이 경우도 2번과 유사하게 동작합니다.
    하지만, 먼 거리일수록 패털티를 크게 부여한다는 점에서 다르게 사용될 수 있습니다.

2-A에 대한 해결방법으로, 유클리드 공간에서의 2번 해결법과 동일합니다.
다만, centroid가 아닌 clusteroid를 사용한다는 차이점만이 존재합니다.

1-B에 대한 해결방법으로 별도의 대표값을 지정하는 것이 아닌, 클러스터 내부의 점들 그 자체를 평가 요소로 사용합니다.
그렇다면 이 경우에는 거리를 측정하는 방법을 찾는게 가장 중요한 요소가 되겠죠?

2-B에 대한 해결방법으로 아래와 같은 방법을 생각해볼 수 있겠습니다.

  • 클러스터 사이의 거리가 가장 짧은 점 2개를 기준으로 거리 측정
  • 클러스터 사이의 거리가 가장 긴 점 2개를 기준으로 거리 측정
    → 이 경우에는 클러스터를 병합했을 때의 생성되는 클러스터의 직경을 의미하며 작을 수록 좋습니다.
  • 모든 점들의 페어에 대한 거리의 평균으로 측정
    → 이 경우에는 클러스터간 점들의 평균 거리를 의미하며 역시 작을 수록 좋습니다.
  • 직경이나 평균 거리를 구한 뒤에 그 안에 들어있는 점들의 개수(밀도)를 측정
    → 이 경우에는 위 방식들과 다르게 새로운 클러스터를 마지한다고 가정하고 진행합니다. 밀도가 높을수록 좋습니다.

이렇게 방법이 많은데 그럼 무슨 클러스터링 방법을 써야 할까요?
답은, 알 수 없습니다.
데이터의 케이스가 굉장히 다양하기 때문이죠..

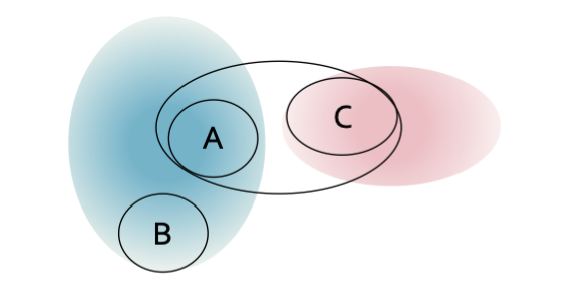
231204-125101

이런 경우에는 centroid 방식으로는 잘 동작합니다. (색칠된 영역으로 클러스터가 병합됩니다)
하지만, 클러스터 사이의 거리가 가장 짧은 점 2개를 기준으로 거리 측정하는 방식으로는 잘 동작하지 않을 것입니다. (A, C 클러스터가 병합해버림)

231204-125304

이런 경우에는 반대로 centroid 방식으로는 잘 동작하지 않을 것입니다.

여기서 알 수 있듯, 계층적 구조는 클러스터링에서 최적해를 보장하지 않는다는 것을 알 수 있습니다.

K-means (Point-assignment) Clustering

K-means 알고리즘은 point-assignment clustering 방식의 대표적인 알고리즘 입니다.
k개의 클러스터를 찾는 알고리즘인데, 위의 계층적 클러스터링 방식과 마찬가지로 최적해를 보장하지는 않습니다.

알고리즘의 동작 방식은 다음과 같습니다.

  1. 일단은 랜덤하게 k개의 중심을 정한다.
  2. 각 점들은 가장 가까운 중심으로 연결한다. (임시 클러스터 생성)
  3. 연결, 즉, 임시 클러스터가 생성되면 임시 클러스터의 점들의 실제 중심으로 중심을 이동시킨다.
    여담으로, 여기서 말하는 중심은 In Non-Euclidean - 1-A에 대한 해결방법 - L2-norm과 비슷하게 거리의 제곱이 최소화 되는 곳을 중심으로 합니다.
  4. 2, 3 과정을 반복하며 클러스터의 centroid가 안정(수렴)되면 종료합니다.

단, k-means 방식은 결과 또한 보장받을 수가 없는게, 초기값의 영향을 많이 받기 때문에 무한루프에 빠질 가능성이 있기 때문입니다.
아래의 예시가 그러한 경우입니다.

231204-130321

따라서 이런 경우를 방지하기 위해 실제 점을 초기값으로 잡거나, k-means++ 방식을 사용합니다.

K-means++


랜덤 중심을 정할 때, 이미 선택된 랜점 중심을 고려해서 고르자는 아이디어에서 출발하는 개선 알고리즘 입니다.
이미 선택된 랜덤 중심으로부터 거리가 멀 수록 선택 확률을 높이는 방식으로 동작합니다.

vs. Hierachical

계층적 클러스터링과 비교했을 때, K-means의 장점은 거리 비교 횟수가 적다는 것입니다.
계층적 클러스터링 방식은 점들마다 다른 점들의 개수 만큼의 비교 횟수가 필요합니다.
하지만, k-means 방식은 점들마다 centroid의 개수 만큼의 비교 횟수만이 필요하기에 빠르게 군집화를 달성할 수 있습니다.

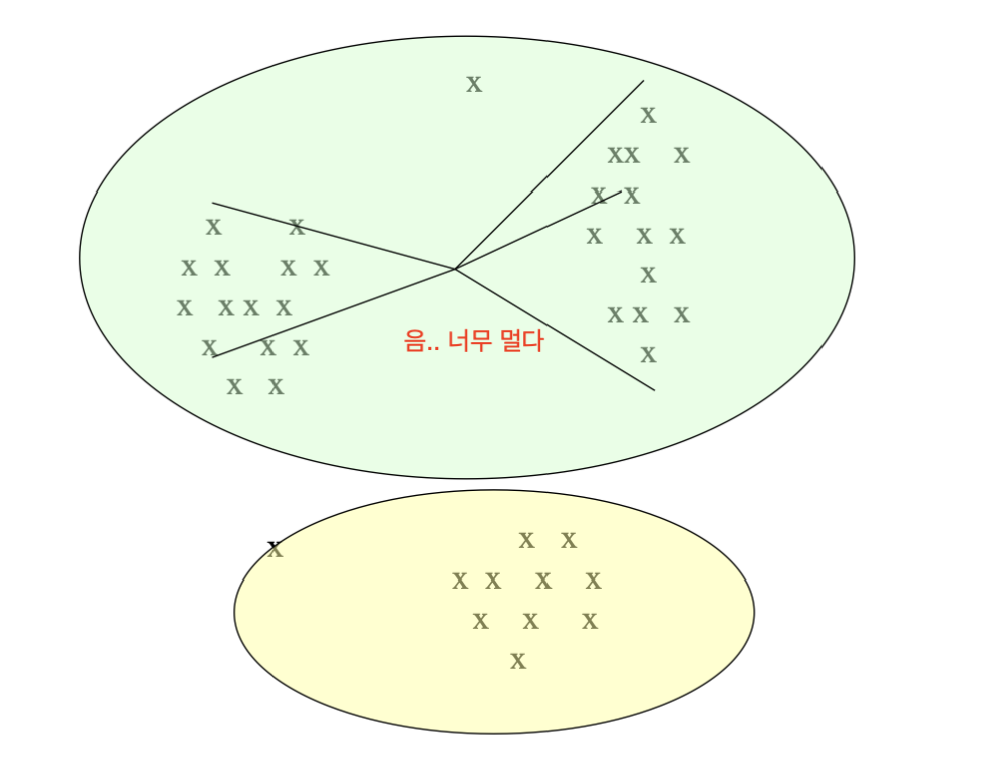
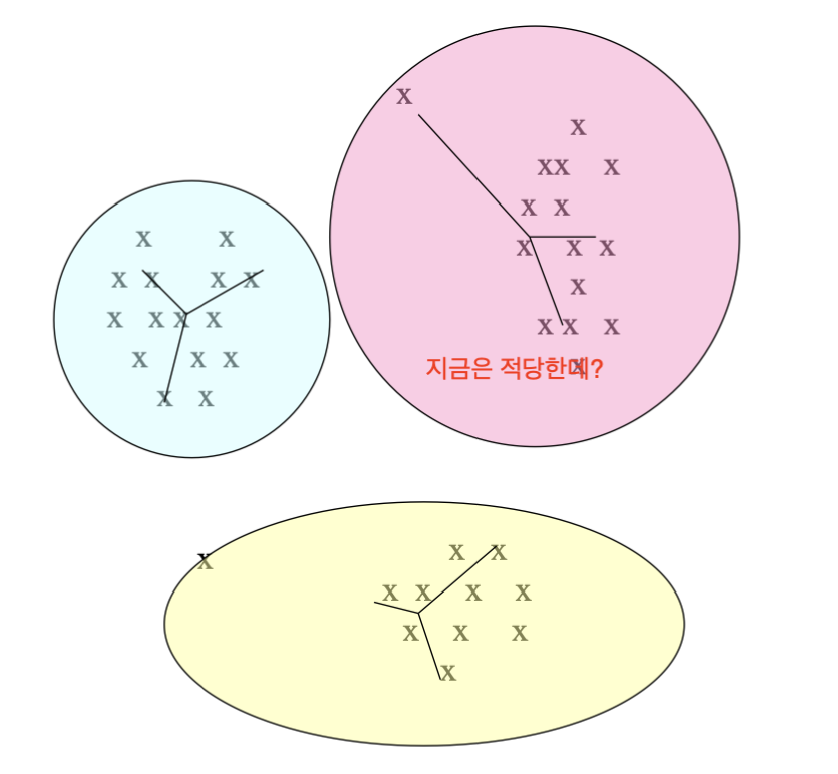
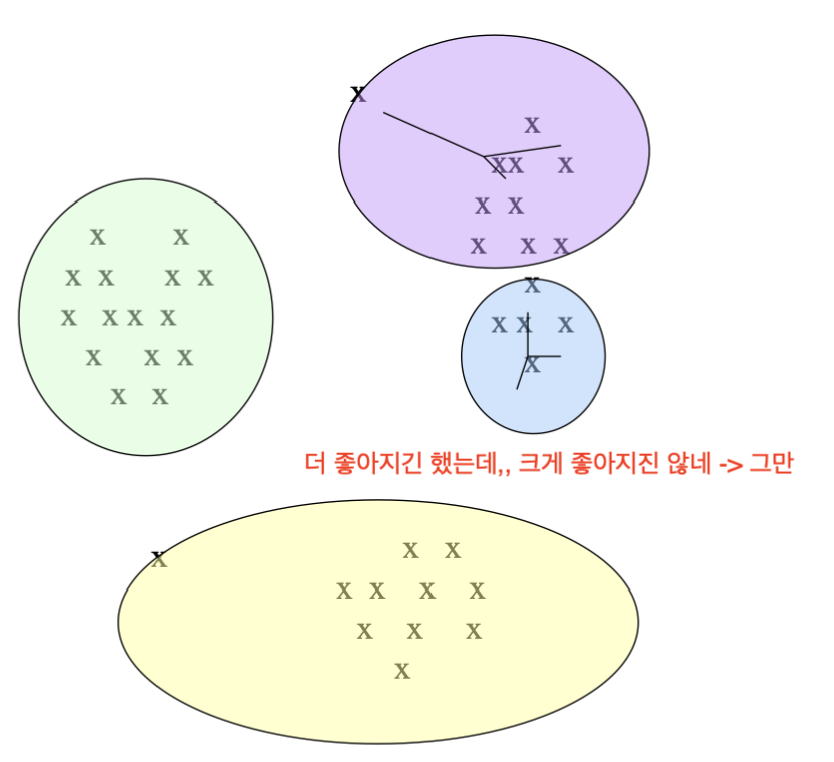
Getting the k right

그렇다면 k 개수는 어느정도로 설정하는 것이 좋을까요?

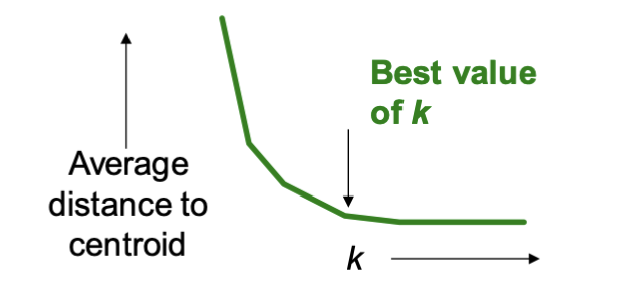
231204-131006

centroid 까지의 거리가 유의미한 수준으로 줄어드는 정도에서 멈추는 것이 좋습니다.
즉, 거리가 줄어들긴 해도 유의미한 수준으로 줄어들지 않는다면 그 시점의 k의 개수를 선택하는 것입니다.

231204-131019
231204-131033
231204-131046