웅덩이

검색 엔진을 개발할 때, 인터넷의 웹 페이지들을 사용자에게 제공함에 있어, 중요한 페이지를 우선적으로 노출시켜 주는 것이 중요합니다.
이 때, 어떤 페이지가 중요한지를 어떻게 알 수 있을까요?

PageRank

PageRank가 높으면 중요한 페이지로 인식을 하게 됩니다.
이제, 페이지에 PageRank를 매기는 방법을 알아봅시다.

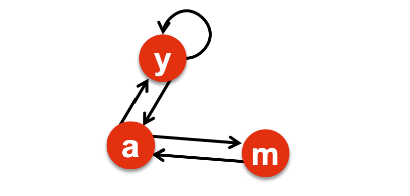
231206-230644

우선 인터넷은 방향 그래프의 형태로 표현 가능합니다.
여기서 중요한 페이지는 무엇일까요?

중요한 페이지는 아래와 같은 특징이 있습니다.

중요한(믿을만한) 정보는 중요한 정보를 서로 가리키는 경향이 있음
특정 query에 대한 링크를 많이 갖고 있는 페이지는 해당 query의 중요한 응답 페이지임

이를 in-link로 정리하면 다음과 같아집니다.

중요한 페이지는 in-link가 많음
같은 in-link 개수라도, 중요한 페이지로부터 오는 in-link가 많을수록 중요한 페이지임

in-link / out-link

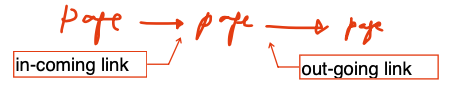
231206-231125

Surfer model

그렇다면 in-link의 개수와 세기를 이용해서 페이지의 중요도를 파악해야 하는데, 어떤 방식으로 파악하는 것이 좋을까요?
그에 대한 하나의 해답으로 surfer model이 있습니다.

동작 방식은 다음과 같습니다.

랜덤한 페이지들에 surfer를 배치
한 스탭마다 페이지의 out-link로 surfer 들을 이동
2번 반복
surfer들이 페이지들에 특정한 분포로 수렴하도록 이동함

여기서 중요한 점은 초기에 surfer를 어떻게 배치하더라도 결국은 특정한 분포로 페이지들에 분포하게 된다는 것입니다.
(마치 자연계의 생물 개체수가 일정 비율로 유지되듯...)

그렇다면 2번에서 surfer를 어떻게 이동시키는 걸까요?
위의 예시를 이용해서 알아봅시다.

231206-230644

$r_i$ 를 페이지 i의 rank라고 하고 페이지 y, a, m의 rank를 계산하면 아래와 같습니다.

r_y = r_y/2 + r_a/2 \\ r_a = r_y/2 + r_m \\ r_m = r_a/2

각 페이지로 in-link되는 페이지의 1/out-degree 의 합으로서 표현되며, 수식화하면 아래와 같습니다.

r_j = \sum_{i \to j} \frac{r_i}{d_i}

그렇다면 PageRank는 위에서 나온 3개의 식을 연립하여 계산하면 됩니다... 만,
해가 무수히 많이 나오는 문제가 있습니다.
따라서 $\sum{r_i} = 1$ 이라는 제약 조건을 달아서 계산하면 됩니다. (1말고 다른것도 가능하지만, 1이 쉬워서..)

하지만, 이 경우 시간복잡도가 $O(n^3)$ 이 나오기 때문에 현실세계에선 사용하기 어렵습니다.
따라서 행렬로 계산하는 것이 좋습니다.

1 \begin{bmatrix} r_y \\ r_a \\ r_m \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0\\ \frac{1}{2} & 0 & 1 \\ 0 & \frac{1}{2} & 0 \end{bmatrix} \begin{bmatrix} r_y \\ r_a \\ r_m \end{bmatrix}

r = M \cdot r

여기서 1은 $\sum{r_i} = 1$ 에서 나온 제약 조건입니다.

즉, 이렇게 하면 앞에서 글로만 적었던 Surfer model의 동작방식을 알고리즘화 할 수 있습니다.

Set r = [1/N, 1/N, 1/N]
r' = Mr
r = r'
Goto 2

참고삼아 방향성이 없은 graph 모델의 경우 PageRank는 아래와 같은 수식으로 구할 수 있습니다.

r_v = \frac{d_v}{2m}

여기서 $d_v$ 는 노드 v에 연결된 edge의 수를 의미하고, m은 전체 edge의 수를 의미합니다.

Degree(in-link)가 높다고 PageRank가 항상 더 높은 것은 아닙니다.

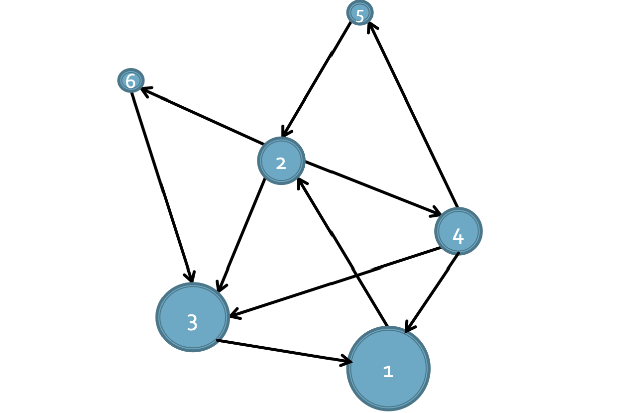
231206-233606

위 경우에는 3의 PageRank가 더 높을거 같지만, 1이 더 높게 측정됩니다.

Google formulation

기존 surfer model에는 치명적인 문제가 있습니다.
바로 Dead-end, Spider-trap 문제입니다.

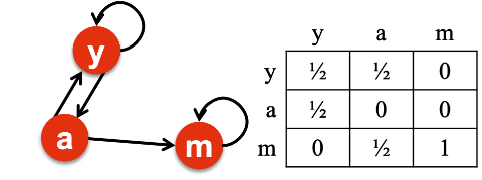
231206-233818

이 경우 페이지 m이 spider-trap입니다.
다른 페이지로의 out-link가 없고 특정 circle에 같히기 떄문이죠.
이련 경우에는 PageRank 계산시 $r_m = 1$ 이 되어버리고, 나머지는 0이되는 문제가 발생합니다.

231206-233954

이 경우 페이지 m이 dead-end입니다.
out-link가 아예 존재하지 않아 surfer가 이동하지 못하고 소멸하기 때문이죠.
이런 경우에는 PageRank 계산시 모두 0이되는 문제가 발생합니다.

이런 현실세계의 문제를 해결하기 위해 Google에서 개선한 알고리즘이 바로 이것입니다.

spider-trap을 예방하기 위해 일정 확률(대충 0.1~0.2)로 링크로 연결된 페이지가 아닌 아예 생뚱맞은 페이지로 surfer를 점프
dead-end의 경우(out-link가 없는 경우) surfer를 생뚱맞은 페이지로 점프

이를 반영한 PageRank 수식은 다음과 같습니다.

r_j = \sum_{i \to j} \beta \frac{r_i}{d_i} + (1-\beta)\frac{1}{N}

앞에 $\frac{r_i}{d_i}$ 부분은 위와 동일합니다.
다만, $\beta$ 의 확률로만 적용됩니다. (대략 0.8~0.9)

나머지 0.1~0.2의 확률로는 N개의 페이지 중 하나로 이동하는 방식을 적용한 것입니다!

그럼 여기서 의문점이 듭니다.

spider-trap은 해결한거 같은데 dead-end는요?

spider-trap인지 아닌지는 판단할 수 있는 방법이 없기 때문에 위와 같이 확률에 의존하여 해결하였지만,
dead-end인지 아닌지는 판단할 수 있는 방법이 존재합니다. (단순히 out-link의 개수가 0이면 dead-end)
따라서 dead-end의 경우에는 그냥 surfer를 다른곳으로 점프시키면 됩니다.

위 식을 행렬식으로 변환해볼까요?

\begin{bmatrix} r_y \\ r_a \\ r_m \end{bmatrix} = (0.8 \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0\\ \frac{1}{2} & 0 & 1 \\ 0 & \frac{1}{2} & 0 \end{bmatrix} + 0.2 \begin{bmatrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \end{bmatrix})\begin{bmatrix} r_y \\ r_a \\ r_m \end{bmatrix}