웅덩이

생김새가 비슷한 사이트를 묶거나, 표절 검사를 하거나, 비슷한 내용의 뉴스를 클러스터링 하는 등 여러 분야에서 사용될 수 있는 기술에 대해 설명합니다.

생김새가 비슷한 문서를 찾아내는 기술이지, 비슷한 토픽을 찾아내는 기술은 아닙니다.

아래의 단계를 거쳐 비슷한 문서를 찾게 되는데, 각 단계에 대한 세부적인 내용은 추후에 설명합니다.

Shingling을 통해 데이터(문서)를 집합으로 변환
Minhashing을 통해 큰 집합을 작은 시그니처로 변환
LSH를 통해 시그니처를 분류 후 비슷한 집합 찾기

Jaccard Similarity

세부내용 설명 전 개념 하나만 짚고 넘어가자.
유사도를 검사할 때, 다음과 같은 경우를 고려해보자.

A, B 모두 메이져한 게임들을 주로 플레이하고, A는 RPG를, B는 FPS를 주로 플레이한다고 가정하자.
이 때, 마이너한 장르의 게임을 예시로 들며 유사도를 검사하는데, A, B 모두 해당 게임을 보유하지 않는다고 두 사람의 유사도가 높다고 이야기 할 수 있을까?
두 사람은 그런 마이너한 장르의 게임에 관심이 없어서 갖고있지 않을 뿐인데, 둘 다 갖고있지 않다고 두 사람의 플레이스타일이 유사하다고 판단하는 것은 무리가 있다.

따라서 이런 유사도 파악의 오류를 해결하기 위해 Jaccard 유사도를 사용하여 유사도를 측정하게 된다.

Sim(C_1, C_2) = \frac{|C_1 \cap C_2|}{|C_1 \cup C_2|}

즉, 두 사람 중 한 사람이라도 해당 게임을 보유하고 있는 경우에만 두 사람이 동시에 해당 게임을 보유하는가로 유사도를 검사하는 것이다.

Shingling

문서의 유사도를 측정할 때 그 기준이 되는 토큰을 생성하는 방법입니다.
k-shingle 과 같은 용어를 사용하는데, 이는 k개의 문자로 이루어진 shingle을 의미합니다.
실제로 비슷한 문서를 싱글링 했을 때 집합의 원소도 일치하는 부분이 매우 많습니다.

예로 들어 "The dog which chased the cat" 이라는 문장이 있다고 했을 때, 여기서 2-shingle를 구하면 다음과 같습니다.

th(보통 소문자로 변환), he, e_, _d, do, og, ...

하지만, 2-shingle로 하면 th, he, do와 같이 문장으로 볼 때는 상당히 유니크한 의미를 갖는 문장이 이렇게 아무데서나 나올법한 shingle이 되어버립니다.
따라서 보통은 8~10-shingle로 하는 것이 적당합니다.

Tokens

10-shingle을 사용하는 경우에는 최대 $27^{10} \approx 200조$ 개의 싱글이 생성되게 됩니다.
이를 메모리상에서 관리하는 것은 현실적으로 불가능한 일입니다.

따라서 싱글을 해싱하여 4bytes의 자료형으로 변환하여 Token으로서 사용하게 됩니다.
4bytes로 최대 약 42억개의 서로 다른 싱글을 표현할 수 있습니다.
물론 다른 싱글에 대해 같은 토큰이 생성될 수 있지만, 그리 빈번한 경우는 아닐 것이며, 효율상 이 방법이 더 좋습니다.

즉, 같은 토큰을 보유한 문서가 있다면, 그 문서들은 같은 싱글을 갖고있다는 얘기이므로, 유사도가 있다고 판단할 수 있겠습니다.

Minhashing

Minhashing을 알아보기 전, 데이터를 표현하는 행렬을 읽는 법을 알고가자.

(token)	$C_1$	$C_2$
a	0	0
b	1	0
c	0	1
d	1	1

a 토큰(싱글)은 문서(Column) 1, 2에서 모두 없다는 뜻이고, b는 문서 1에서만 갖고있다는 뜻으로 해석하면 된다.
참고로 위의 경우 두 문서의 Jaccard 유사도는 1/3이다. (a는 둘 다 없기에 비교대상이 아니다)

Permute the rows

우선 행을 핸덤으로 뒤죽박죽 섞는다.
섞는다는 것은 실제로 맊 섞는다는 것이 아닌, 탐색 순서를 섞는다는 것을 의미하는데, 구현 관점에서 해싱을 돌리는 것과 같다.
예시를 보며 이해해보자.

(row)	$C_1$	$C_2$	$C_3$
1	0	1	1
2	1	0	1
3	0	1	0
4	0	0	0
5	1	0	1

$h_1(x) = x \% 5$ 해시함수를 적용하면 탐색 순서는 다음과 같아진다.

5(0) → 1(1) → 2(2) → 3(3) → 4(4)

$h_2(x) = (2x+1) \% 5$ 해시함수를 적용하면 탐색 순서는 다음과 같아진다.

2(0) → 5(1) → 3(2) → 1(3) → 4(4)

Create signature

탐색 순서에 맞게 처음으로 1(토큰 보유)을 만나는 탐색 순서를 기록한다.

$h_1$ 를 적용한 탐색시 생성되는 Singature matrix
[1, 2, 1]

$h_2$ 를 적용한 탐색시 생성되는 Singature matrix
[1, 3, 1]

즉, $C_1$ 에 대한 시그니처는 11, $C_2$ 는 23, $C_3$ 은 11이 된다.

여기서 중요한 특징이 있는데, 시그니처의 길이가 길어질 수록(무작위 순서에 의한 탐색 횟수가 늘어날 수록) 시그니처가 일치할 확률이 Jaccard 유사도와 확률이 같아진다.
그 이유를 간단한 예시로 이해해보자.

우선, $C_2$ 과 $C_3$ 의 Jaccard 유사도는 1/4이다.
그런데 이 때, Singature가 같아지는 경우는 무엇일까? 바로 최초로 1이 나오는 시점이 같다는 이야기이다.
즉, 같은 row에 대해 둘 다 1이 들어가 있는 row를 고를 확률과 같아진다.
둘 다 0인 경우를 제외하면 4개 중에 둘 다 1인 row는 1개 존재하기에 Jaccard 유사도와 동일한 1/4 확률을 갖는다.

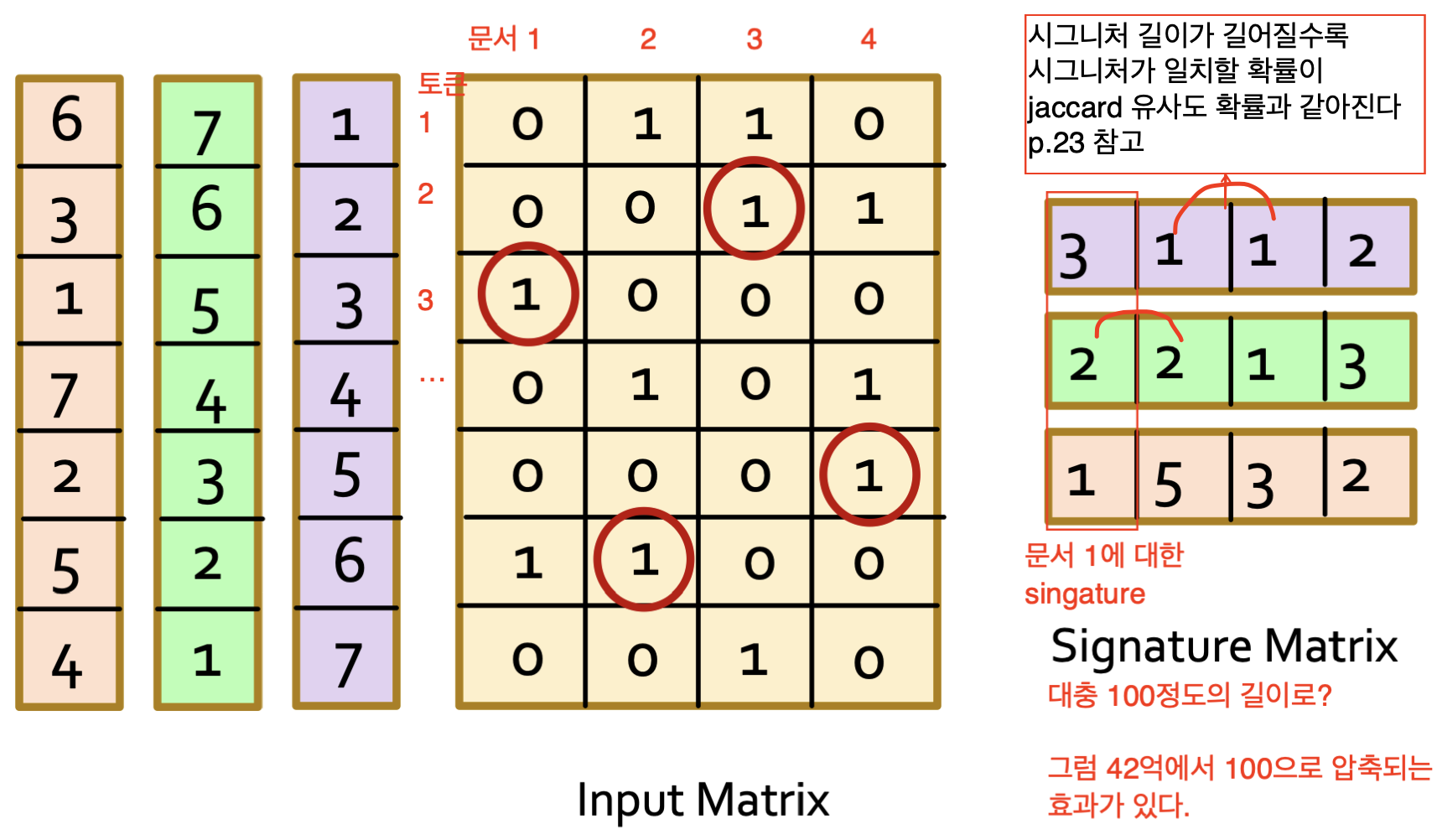
231020-235719

이해를 돕기 위해 다른 예시도 보자.

원래대로라면 생성되는 모든 토큰(42억개)에 대해 유사도를 검사 했어야 했다.
하지만, 시그니처를 만드는 과정에서 무작위 순서로 탐색을 진핼할 때, 탐색개수를 제한을 걸면 검사 시간을 줄일 수 있다.
예로 들어 해시함수의 결과를 50까지만 검색한다면 42억개의 항목에 대해 검사를 진행하지 않아도 된다.

이 때 검사 개수를 줄인 만큼 서로다른 해시를 여러 번 진행하면 신뢰도 역시 어느정도 확보할 수 있다.
예로 들어 서로 다른 해시함수 100개를 적용한다면, 시그니처의 길이가 100으로 결정되는데, 이 길이는 충분히 신뢰도를 확보할 수 있을 것이다.
즉, 42억개에서 100개로 압축되는 효과가 발생하는 것이다.

위의 사진을 예시로 실제 Jaccard 유사도와 시그니처 유사도를 비교해보며 시그니처 길이가 신뢰도에 어느정도 영향을 주는지 알아보자.

Column 1, 2
Jaccard Similarity: 1/4
Singature Similarity: 1/3

Column 2, 3
Jaccard Similarity: 1/5
Singature Similarity: 1/3

Column 3, 4
Jaccard Similarity: 1/5
Singature Similarity: 0

implement

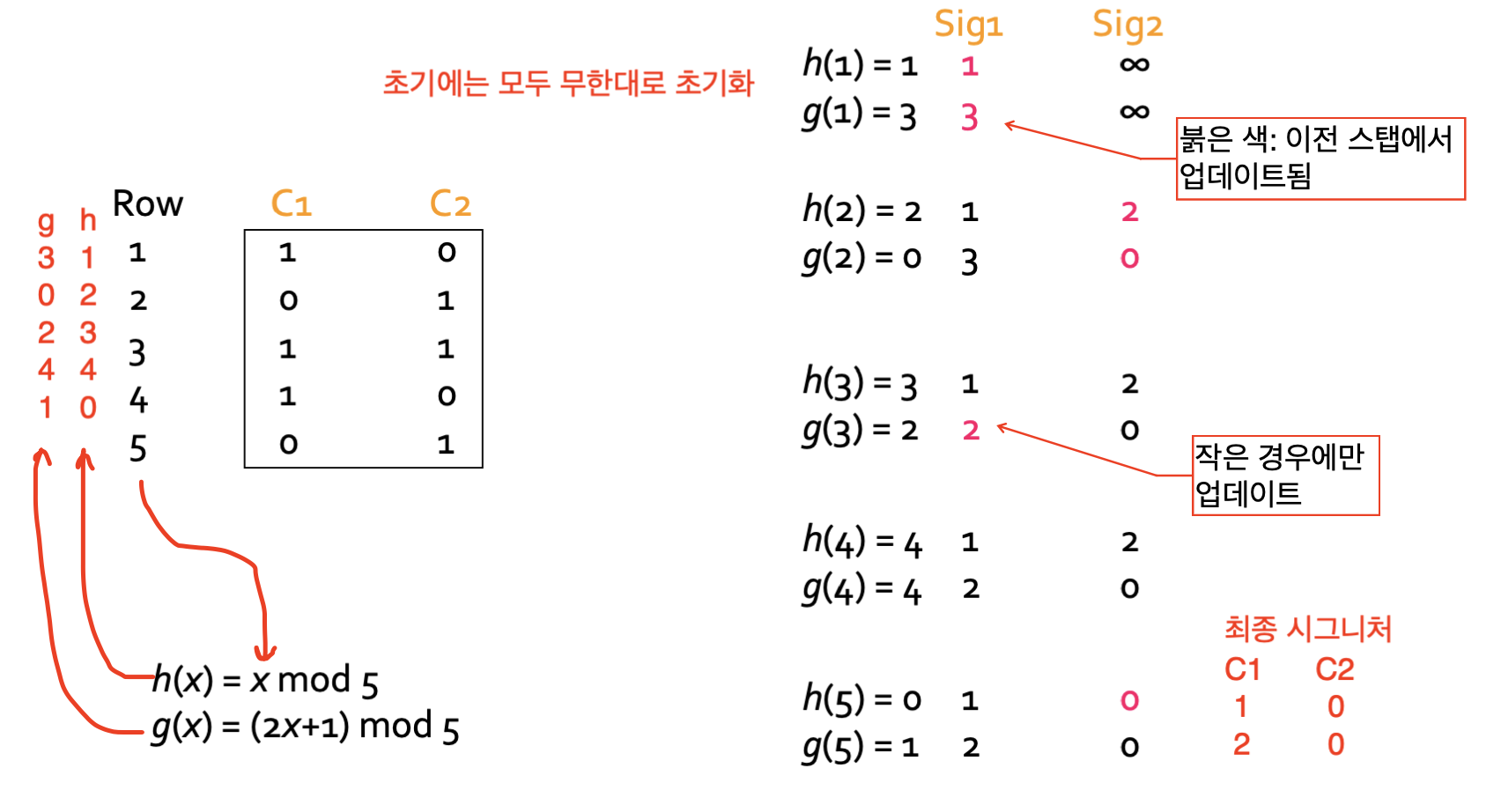
의사코드로 구현해보고 시그니처 생성과정을 살펴보자.

의사코드

// 처음에 무한대로 초기화
for (all i and c) M(i, c) = inf;

// 각 행에 대해 반복하는데, 여기에 탐색개수 50개와 같은 제한을 걸 수 있음
for (each row r) {
  for (each hash function h_i) {
    compute h_i(r);
  }
  for (each column c) {
    // 탐색지점에 1이 있는 경우
    if (c has 1 in row r) {
      for (each hash function h_1) {
        // 저장된 시그니처보다 새 탐색값이 작은 경우에만 업데이트
        if (h_i(r) is smaller them M(i, c)) {
          M(i, c) = h_i(r);
        }
      }
    }
  }
}

231021-001859