Frequent Itemset
빈발 항목 집합을 구하는 방법을 알아봅니다.읽는데 17분 정도 걸려요.Naive Algorithm
우선 나이브한 방법으로 빈발 항목 집합을 찾는 방법부터 알아보자.
처음에는 frequent pair를 찾는 것을 목표로 하고, 이후에 원소의 개수가 더 많은 집합을 찾는 방식으로 확장하자.
간단하게 요약하면 아래의 두 단계에 걸쳐 모든 pair를 생성한다.
- 가능한 모든 조합의 쌍 생성
n개의 아이템이 들어있는 Basket에서는n(n-1)/2개의 조합 쌍이 생성된다. - 해당 조합 쌍이 동시에 등장하는 경우 1씩 카운트하며 개수를 센다.
이 방식은 구현이 제일 간단하지만 치명적인 문제가 있다.
개수를 4bytes의 int형으로 저장한다고 가정하면 n개의 아이템이 존재하는 Basket에 대해 2n(n-1)bytes의 메모리 공간이 할당되어야 하는데, 이런 크기의 메모리 공간을 할당할 수 없을 뿐더러, 존재하지도 않은 페어의 메모리 공간을 할당해야만 하는 문제점이 있다.
Triples
이런 한계를 극복하기 위해 원소를 triples로 관리하는 기법도 있다.
[i, j, c] 로 관리하는 기법인데, "{i, j} 페어가 c번 등장함" 이라는 의미로 관리하는 것이다.
이렇게 하면 하나의 페어당 12bytes가 들어가긴 하지만, 존재하지도 않은 페어에 대한 메모리 공간 할당은 방지할 수 있다.
하지만 메모리 주소 관리를 위해 별도의 해시 테이블을 할당해야 하기에 그다지 메리트가 크지는 않다.
Triples 방식이 더 효율적으로 작동하기 위해서는 가능한 모든 페어 조합 수의 1/3 수준으로 실제로 등장하는 페어수가 존재해야 한다.
A-Priori Algorithm
페어가 메인 메모리에 올라갈 정도로 적다면 나이브한 방식을 사용하는것이 좋다.
Basket을 한 번만 읽어도 되는, 1pass만에 빈발 항목 집합을 찾을 수 있으니 속도가 빠르기 때문이다.
pass
Basket(파일)을 처음부터 끝까지 읽는 횟수로, Disk I/O의 cost가 큰 만큼 pass 횟수에 따라 알고리즘의 성능을 평가하는 요소로 작동한다.
하지만, 그렇지 않은 대다수의 경우에는 다른 방식을 고안해야 한다.
A-Priori 알고리즘의 경우에는 2pass로 pair를 찾을 수 있지만, 그 대신 메모리 효율성이 극대화되어 매우 큰 파일도 메모리에 적재할 수 있다.
하지만 이게 어떻게 가능한 것일까?
기본적인 아이디어는 이렇다.
이 파일에는 아이템이 a, b, c 이렇게 존재한다고 해보자.
만약 {a, b} 가 10번 등장했다면, 진 부분집합 {a}, {b} 역시 10변 이상 등장했을 것이다.
반대로 말하면 {a}, {b} 가 10번도 안나왔다면, {a, b} 역시 10번도 안나올 것이다.
따라서 빈발 항목 집합을 세기 전에 우선 threshold보다 큰 경우에만 빈번하다고 기준을 정의하고 시작한다.
Pass 1
pass 1에서는 우선 파일을 읽어보며 개별적인 아이템 개수부터 세어본다.
이 때, 아이템 개수가 threshold보다 큰 경우에만 다음 pass에서 고려하게 된다.
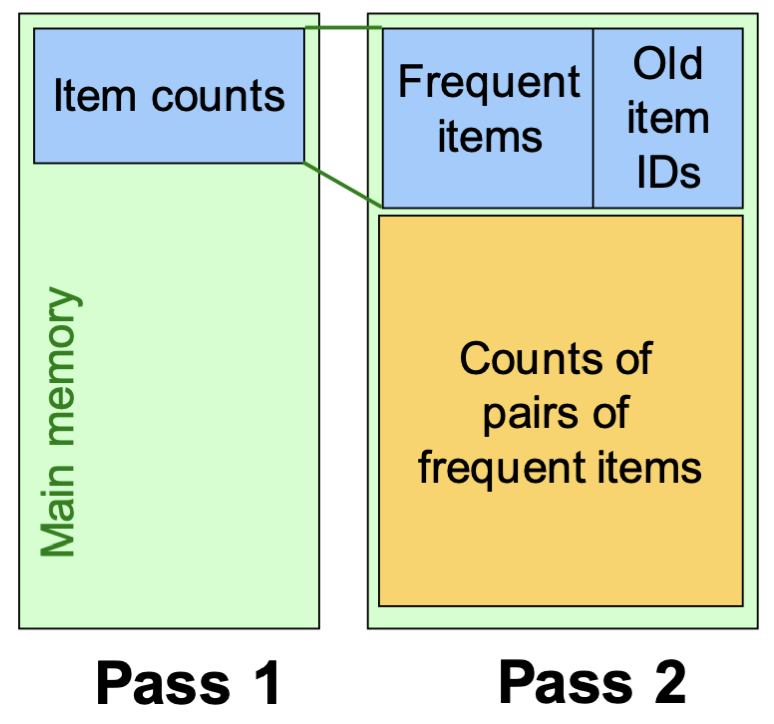
참고로 pass 2에서 빈번하게 등장한 아이템에 접근하기 위해 빈번하게 등장한 아이템들의 주소를 저장하기 위해 메모리 공간을 약간 할당한다.
Pass 2
pass 2에서는 pass 1에서 통과한 아이템들을 이용해서 페어를 생성한다.
그리고 나이브한 방법과 마찬가지로 파일을 읽으면서 등장 횟수를 카운트한다.
이 방식이 훨씬 효율적인게, 만약 pass 1에서 읽어야 할 아이템의 개수가 1/10 으로 줄었다면,
pass 2에서 생성되는 pair의 개수는 1/100 수준으로 줄어든다.
따라서 메모리 효율성이 거의 100배 증가하는 것이다.
Frequent Triples
pair에서 확장되어 원소의 개수가 3개, 4개인 경우의 처리 방식도 알아보자.
근데 사실 별 거 없다. 그냥 앞에서 봤던 방법의 반복이다.
빈번하게 등장한 페어를 이루는 아이템들로 triple을 만든다.
이후 각 triple의 진 부분집합이 빈번하게 등장한 pair인 경우에만 파일을 읽어보며 세어보면 된다.
예시들 들어 이해해보자.
= {{b} {c} {j} {m} {n} {p}}
threshold보다 많이 등장한 원소는 아래 4개라고 해보자.
= {b, c, j, m}
을 이용해서 다름 pass 진행= {{b, c} {b, j} {b, m} {c, j} {c, m} {j, m}}
threshold보다 많이 등장한 원소는 아래 4개라고 해보자.
= {{b, c} {b, m} {c, j} {c, m}}
을 이용해서 다름 pass 진행= {{b, c, m} {b, c, j} {b, m, j} {c, m, j}}
이 때 {b, c, j} {b, m, j} {c, m, j}의 부분 집합은 에 포함되지 않으니 세어볼 필요 없음 (반드시 threshold보다 적게 등장할 것)
즉, A-Priori 알고리즘은 k-pass 단계에서 k-tuple의 집합을 생성하게 되는데,
일반적으로 k=2일 때, 메모리 사용량이 가장 많다.
PCY Algorithm
Park-Chen-Yu 알고리즘으로 A-Priori 알고리즘의 pass 1에서 메모리의 빈 공간을 활용하여 탐색 효율을 높인 알고리즘이다.
그 이후의 과정은 A-Priori와 같으니, pass 1에서의 메모리 관리 방법에 대해서만 알아보자.
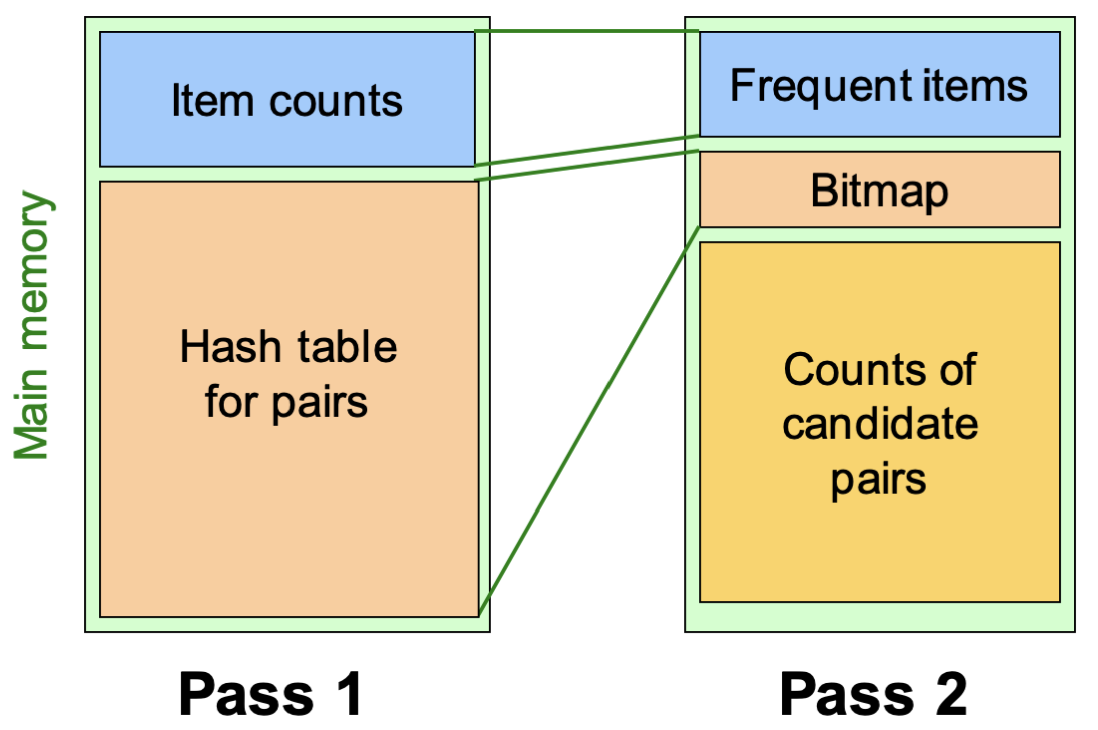
Bucket's Hash Table
pass 1에서 개별적인 아이템 등장 횟수를 카운트 할 때, 동시에 아이템으로 만들 수 있는 pair의 개수도 동시에 카운트 하는 것이다.
이 때 페어를 해싱하여 버킷으로 만들고, 그 버킷을 Hash table for pairs에 최대한 가득 채운다.
예로 들어 a, b, c의 개수를 세어보면서 {a, b} {b, c} {a, c}를 해싱한 주소에 등장할 때 마다 1씩 카운트 하는 것이다.
만약 {a, b} {a, c} 의 해시 결과가 같은데, 해당 pair을 해시한 곳의 값이 threshold보다 작다면 pass 2에서 {a, b} {a, c} 를 셀 필요가 없다는 뜻이된다.
그럼에도 불구하고 pass 2에서는 파일을 한 번 더 탐색을 해야만 하는데, 버킷만으로 pair가 threshold보다 크다고 단정지을 수 없는 이유는 해시의 특성 때문이다.
다른 입력에 대해 같은 출력이 나올 수 있는 해시는 여러 pair가 하나의 버킷에 카운트 될 수 있음을 시사한다.
즉, 버킷이 threshold보다 작다면 해싱후 그 버킷을 가리키는 pair는 세어볼 필요가 없지만,
threshold보다 큰 경우에는 threshold보다 작은 값이 여러개 모여 threshold보다 커졌을 가능성이 있기 때문에 다시 파일을 읽어보며 확인을 해봐야 하는 것이다.
Bit-vector (bitmap)
아무튼, pass 1에서 pair의 해싱을 통한 버킷이 저장된 해시 테이블을 만들어 추후 파일 탐색시 검사해야 할 pair의 수를 줄이게 되는데,
해시 테이블을 암축하지 않으면 pass 2로 넘어갈 수 없다. (메모리에 꽉 차게 할당했기 때문)
어떻게 압축해야 필요한 정보를 유지할 수 있을까?
우리가 필요한 정보는 n번째 버킷이 threshold보다 많이 등장했는지(1) 아닌지(0) 이다.
따라서 해시 테이블에 n번째 버킷이 threshold보다 크다면 1, 아니면 0으로 압축할 수 있다.
4bytes(32bits)에서 1bit로 압축되는 셈이다.
그리고 이제 pass 2에서 {b, c}를 파일에서 몇 번 등장하는지 세어보기 전에 우선 해싱을 하여 bitmap에 해당 해시의 위치가 1이면 실제로 세어보고 0이면 셀 필요 없이 threshold보다 작다는 뜻이 된다.
Random Sampling
지금까지 알아본 빈번 항목 집합을 찾는 방식은 k-tuple의 개수를 세어보기 위해서는 k-pass를 거쳐야만 했다.
이번부터 알아볼 알고리즘은 단 2-pass만에 세어볼 수 있는 방식을 알아볼 것이다.
랜덤 샘플링 기법은 파일을 메모리에 올릴 수 있을 만큼만 적당히 샘플링 해와서 모든 카운트 과정을 메모리 내부에서 해결하는 것이다.
하지만, 샘플링 비율만큼 실제 데이터 양도 줄어들기 때문에 threshold도 샘플링 비율만큼 줄여서 측정한다.
하지만 이 경우에는 False Positive, False Negative 문제가 발생할 수 있다.
False Positive
실제로는 빈번하지 않은데 샘플링된 데이터에서는 빈번하다고 나온 경우
False Negative
실제로는 빈번한데 샘플링된 데이터에서는 빈번하지 않다고 나온 경우
False Positive의 경우에는 pass 2에서 빈번 집합의 경우 실제로 빈번하게 등장하는지 검사해 봄으로써 해결할 수 있다.
하지만 False Negative의 경우에는 찾아낼 방법이 없다.
threshold를 더 작게 설정하는 방식으로 False Negative가 나올 확률을 줄일수는 있겠지만, 해결책은 아니다.
SON Algorithm
기본적인 방식은 랜덤 샘플링과 동일하다.
차이점은 SON Algorithm음 모든 파일을 다 읽는다는 것이다.
즉, 한 번 읽을 때 샘플링한 작은 청크를 읽지만, 이 과정을 여러번 반복해서 전체 파일을 읽어온다는 차이점이다.
이 방식은 False Negative도 없다고 확신할 수 있다.
왜냐하면 실제로 빈번한 집합이라면 읽어오는 모든 청크에 대해 최소 1개의 청크에서는 빈번하게 등장할 것이기 때문이다.
하지만 모든 청크를 결국 메모리에 1번은 올려야 하기 때문에 시간이 오래 걸린다는 단점이 있다.
Toivonen's Algorithm
시작은 랜덤 샘플링과 같다.
하지만 랜덤 샘플링에서 샘플을 파일의 1/100 수준으로 샘플링 한다면 threshold도 1/100 수준으로 설정할텐데 이 경우에는 좀 넉넉하게 1/125 정도로 설정한다는 차이가 있다.
추가로 pass 1에서 Negative Border 라는 개념을 도입하여 False Negative를 방지한다.
이 외에는 랜덤 샘플링 방식과 동일하다.
Negative Border
Negative Border에 포함되는 집합은 본인은 빈번하지 않지만, 본인의 진 부분집합은 빈번하게 등장한 경우 포함된다.
예시를 들어 알아보자.
모든 집합이 {} {a} {b} {c} {a b} {b c} {a c} {a b c} 만 존재한다고 가정해보자.
Case 1{a} {b} 만 빈번하게 등장함 → {a b} {c} 를 Negative Border로 추가.
{a b} 의 경우에는 본인의 진 부분집합이 빈번하게 등장했으니 본인도 빈번하게 등장했을 가능성이 있다.
따라서 추가 검사를 진행해봐야 하는 것이다.
{c} 의 경우에는 진 부분집합이랄게 없기 때문에 추가 검사를 진행해 봐야 하는 것이다.
Case 2{a} {b} {c} 만 빈번하게 등장함 → {a b} {b c} {a c} 를 Negative Border로 추가.
빈번하게 등장한 집합의 다음 스탭만 의심해야지, 나아가서 {a b c} 까지는 검사하지 않는다.
Case 3{} (아무것도 빈번하지 않음) → {a} {b} {c} 를 Negative Border로 추가.
샘플링을 너무 못했을 가능성이 높기에 일단 원소 1개짜리는 추가 검사를 해봐야 한다.
이후 pass 2에서 빈번 항목 집합과 Negative Border에 대해 검사를 진행한다.
False Positive의 경우에는 랜덤 샘플링과 마찬가지로 여기서 걸린다.
False Negative의 경우에는 Negative Border에 포함된 집합을 검사하면서 나오게 될텐데,
만약 Negative Border에 있는 집합이 실제로는 빈번하게 등장했다면 False Negative가 존재한다는 뜻이 된다.
이런 경우에는 다른 샘플로 pass 1부터 다시 시도하게 된다.
따라서 정확히는 2 pass안에 끝나지 않을 수는 있다.