웅덩이

Dimensionality Reduction

차원 축소 방법에 대해 알아보기 전에, 왜 차원축소를 하는걸까요?
다음과 같은 이유들이 있다고 생각합니다.

차원의 저주 해결
데이터 용량 절약
잠재된 관점(축)의 발견

그렇다면 차원 축소는 어떤 원리를 이용해서 하게 되는 걸까요?
아래의 예시를 봐봅시다.

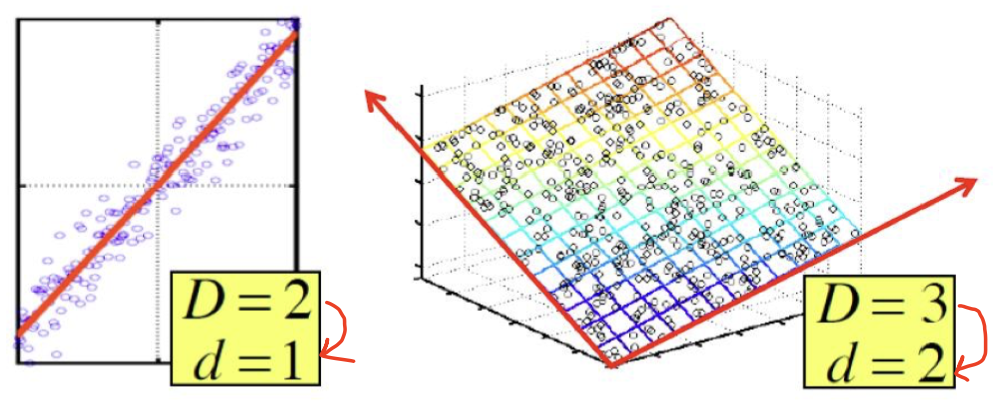
231204-135530

좌측은 2차원 데이터인데 하나의 직선 위에 데이터들이 많이 밀집된 형태를 보입니다.
우측은 3차원 데이터인데 하나의 평면 위에 데이터들이 많이 밀집된 형태를 보입니다.

만약, 직선이나 평면에 데이터들을 적절하게 투영(projection)할 수 있다면?
데이터를 표현하기 위해 2, 3개의 파라미터를 사용해야 했던 것에 반해, 1, 2개의 파라미터 만으로 데이터를 표현할 수 있을 것입니다.

그렇지만, 무턱대고 투영하는 것은 좋지 않습니다.
최대한 데이터의 손실이 적도록 투영하는게 옳은 방법이겠죠?

데이터의 손실이 적도록 차원을 축소하기 위해서는 새로운(낮은) 차원의 축을 잘 선택해야 합니다.
축을 잘 선택하는 방법은 아래와 같은 순서로 진행하면 왠만하면 차원 축소할 때 데이터의 손실이 적을 것입니다.

데이터의 분산이 가장 큰 방향의 축을 선택
1에서 선택한 축의 수직인 방향의 축을 선택
1, 2에서 선택한 축의 수직인 방향의 축을 선택... (반복)

Rank

축을 선택하는 방법은 대강 알 거 같습니다.
그러면 얼마나 축을 뽑는게 좋은걸까요?

답은 행렬의 rank 에 해당하는 만큼 축을 뽑으면 됩니다.

Rank

rank는 선형 독립적인 행의 개수를 의미합니다.

예시와 함께 알아봅시다.

A = \begin{bmatrix} 1 & 2 & 1 \\ -2 & -3 & 1 \\ 3 & 5 & 0 \\ \end{bmatrix}

rank(A) = 2 입니다.
왜냐하면 3행은 1행 - 2행 으로 표현되기 때문에 3행은 선형 종속적인 행이기 때문입니다.

즉, 기존 basis [1 0 0], [0 1 0], [0 0 1] 의 3축에서 [1 2 1], [-2 -3 1] 의 2축으로 차원을 축소할 수 있습니다.
그렇다면 A는 아래와 같이 변형되겠죠?

A_{with\_new\_basis} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & -1 \\ \end{bmatrix}

SVD

3차원은.. 좀만 노력하면 분해할 수 있지만, 30차원이 넘어간다면?
아마 특정 공식에 의존하여 분해하는 것이 좋을 것입니다.
차원을 직접적으로 축소하는 방법은 아니지만, 하나의 행렬을 의미가 담긴 3개의 행렬로 분해하는 방법이 바로 SVD, 고윳값 분해 입니다.

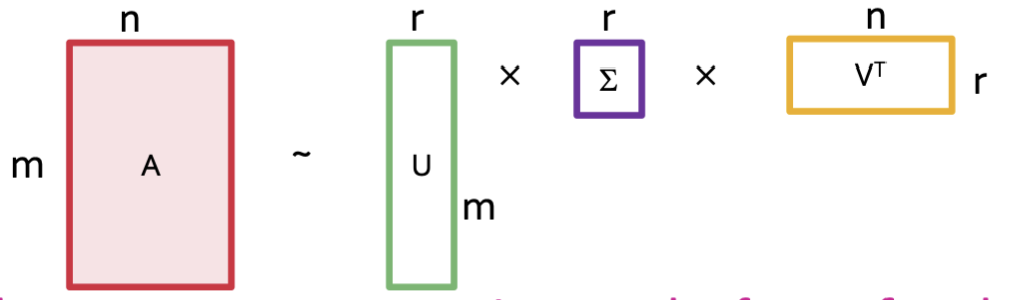
231204-142024

행렬 A는 $U \sum V^T$ 로 데이터 손실 없이 분해됩니다.
다만 차원을 줄이기 위해 r을 보다 작은 값으로 분해하여 약간의 데이터 손실과 함께 차원을 축소하는 것이죠.

아무튼, SVD는 위의 $U \sum V^T$ 형태의 3개의 행렬로 분해하는데, 각각 행렬마다 중요한 특징이 있습니다.
그 특징을 아래의 예시와 함께 살펴보겠습니다.

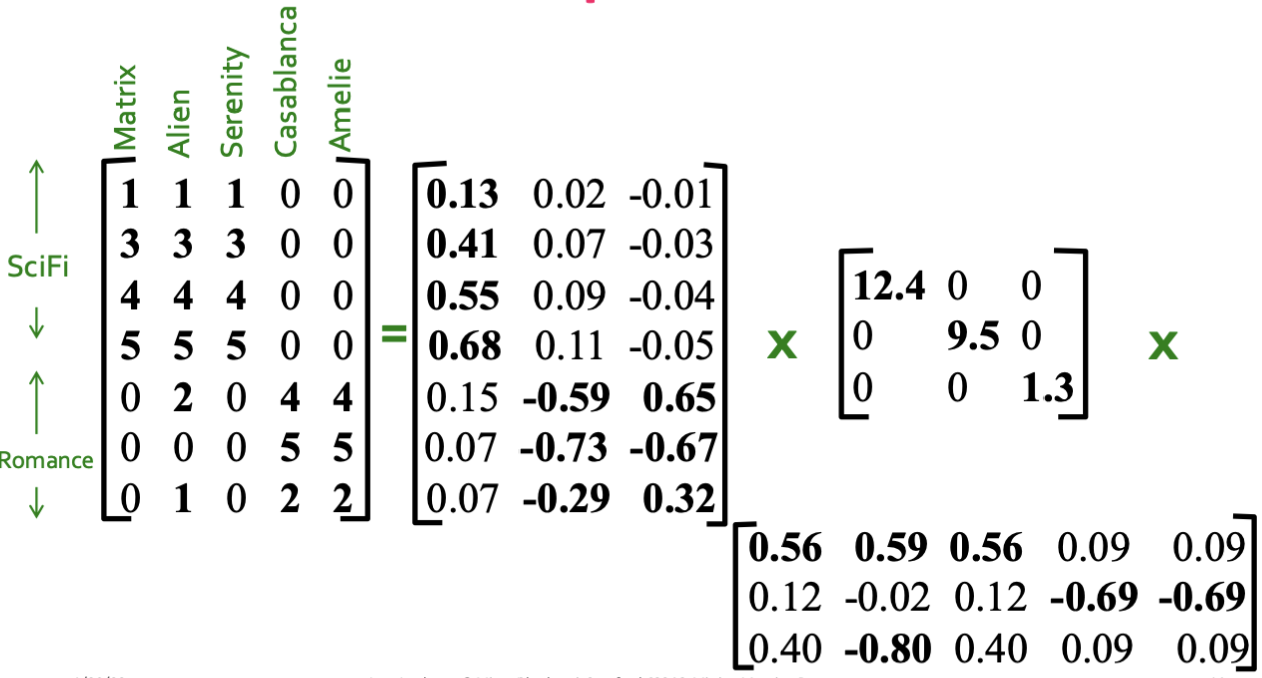
231204-143118

우선 $A$ 부터 살펴보겠습니다.
예시로 든 행렬은 유저가 평가한 영화 평점에 대한 행렬입니다.
예로 들어, 4행의 유저는 SciFi한 영화에는 5점을 남겼지만, Romance 영화는 관심도 없다는 의미겠네요.

다음은 $\sum$ 을 살펴보겠습니다.
$\sum$ 은 대각 행렬로, 원소가 좌상단부터 우하단으로 반드시 내림차순 정렬되어 있습니다.
그렇기 때문에 SVD시 $U \sum V^T$ 가 유일하게 결정됩니다.

여기서 $\sum$ 은 concept의 세기에 대한 정보를 담고 있습니다.

Value	Concept
12.4	Sci-fi
9.5	Romance
1.3	Romance-Alien

즉 데이터들이 Sci-fi, Romance 한 concept에 대해 분산이 크지만,
Romance-Alien 과 같은 잡스러운(?) concept에 대한 분산은 낮음을 알 수 있습니다.
(차후에 이를 이용해 차원 축소를 하게 됩니다)

다음은 $U$ 를 살펴보겠습니다.
이 행렬은 유저에 대한 concept 정보를 담고 있습니다. (별로 안중요함)

마지막으로 $V^T$ 를 살펴보겠습니다.
이 행렬은 영화에 대한 concept 정보를 담고 있습니다. (별로 안중요함)

D.R. with SVD

이제 고윳값 분해 방식과 의미를 알았으니 차원을 실제로 축소해봅시다.

바로 위에서 다음과 같이 언급했었습니다.

즉 데이터들이 Sci-fi, Romance 한 concept에 대해 분산이 크지만,
Romance-Alien 과 같은 잡스러운(?) concept에 대한 분산은 낮음을 알 수 있습니다.

분산이 크다는 것은 해당 축으로 투영시켰을 때, 데이터 손실이 적다는 것을 의미한다고 했었습니다.
즉, $\sum$ 의 값이 작은 부분을 제거한다면?
영향력이 적은 차원을 제거하는 꼴이 되어버려서 차원 축소를 달성할 수 있습니다!

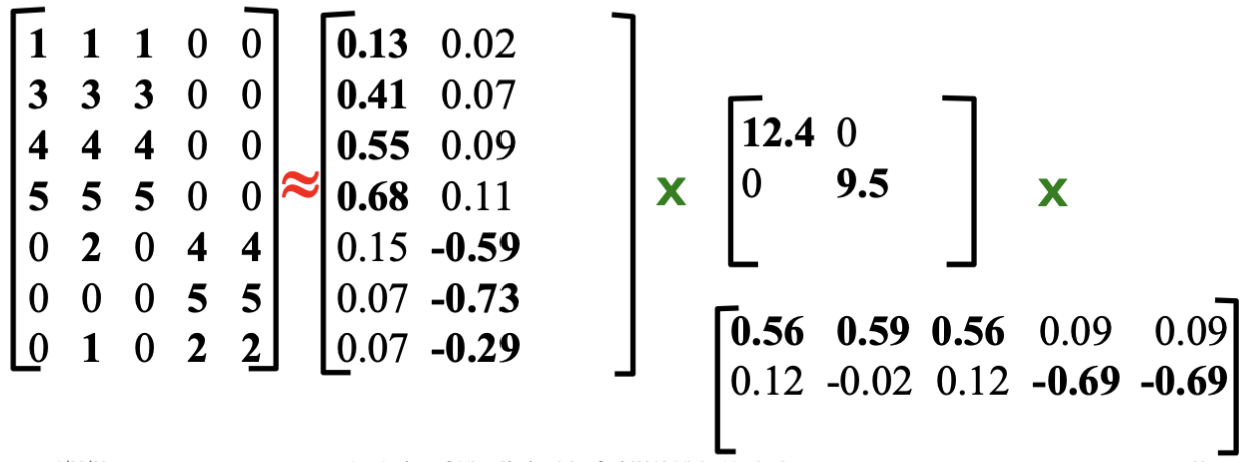
231204-144815

이렇게 SVD로 분해된 세 행렬을 계산하면 다음과 같이 복원할 수 있습니다.

231204-144924

상당히 유사하지만, 데이터 손실 때문에 완벽하게 복원되지는 않았습니다.
즉, 데이터의 손실이 발생할 수 있는 점을 염두하여 차원을 축소해야 합니다.

그렇다면 차원축소는 얼마나 하는것이 좋을까요?

정해진 답은 없지만, 일반적으로 SVD된 $\sum$ 행렬의 에너지(대각선 제곱의 합)의 90% 이상 남기는 것이 좋다고 알려져 있습니다.
예로 들어서 차원 축소 전의 $\sum$ 에너지는 아래와 같습니다.

12.4^2 + 9.5^2 + 1.3^2 = 245.7

Romance-Alien concept를 제거한다면 에너지는 아래와 같이 감소합니다.

12.4^2 + 9.5^2 = 244.01

즉, Romance-Alien concept 차원을 제거하여 축소한다고 해도 원본의 99%에 해당하는 에너지가 해당되기에 차원을 축소해도 데이터 손실이 거의 없습니다.
하지만, 여기에서 Romance concept까지 제거한다면?

12.4^2 = 153.76

62.6%의 에너지밖에 남지 않습니다.
즉, 차원을 많이 줄일수는 있지만, 복원했을 때 유의미한 데이터를 얻을 수는 없을 것입니다.

Application

이제 실제 예시와 함께 분석하는 방법을 알아봅시다.

231204-144815

위와 같이 관리되고 있는 추천 시스템 데이터에서 "Matrix" 와 같은 SciFi concept의 영화를 좋아하는 유저를 찾고싶다고 해봅시다.

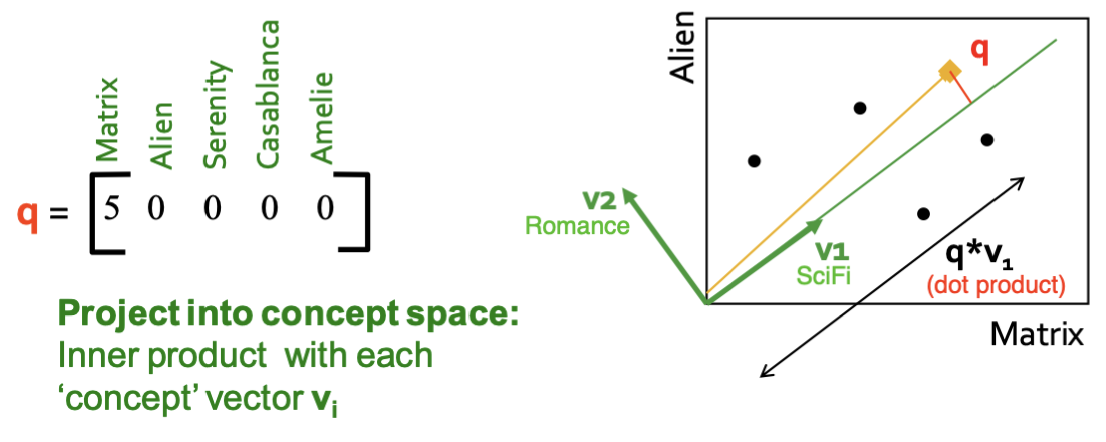
231204-150645

그럴 때는 유저 벡터를 concept-space에 투영해서 그 방향(경향)을 비교하는게 좋습니다.
그리고 그 투영을 구하는 방법은 $q \cdot V_{concept}$ 이죠.

예로 들어 아래와 같은 유저 p, q의 영화 성향이 같은지 다른지를 판단해봅시다.

p = \begin{bmatrix} 5 & 0 & 0 & 0 & 0 \end{bmatrix}

q = \begin{bmatrix} 0 & 4 & 5 & 0 & 0 \end{bmatrix}

Jaccard 유사도, LSH와 같은 방식을 사용한다면, 두 사람은 전혀 다른 취향을 가진 사람이라고 판단할 것입니다.
하지만, $q \cdot V$ 을 이용하여 concept 벡터를 만들어 비교해본다면 어떨까요?

p_{concept} = \begin{bmatrix} 5 & 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0.56 & 0.12 \\ 0.59 & -0.02 \\ 0.56 & 0.12 \\ 0.09 & -0.69 \\ 0.09 & -0.69 \end{bmatrix} = \begin{bmatrix} 2.8 & 0.6 \end{bmatrix}

q_{concept} = \begin{bmatrix} 0 & 4 & 5 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0.56 & 0.12 \\ 0.59 & -0.02 \\ 0.56 & 0.12 \\ 0.09 & -0.69 \\ 0.09 & -0.69 \end{bmatrix} = \begin{bmatrix} 5.2 & 0.4 \end{bmatrix}

p, q 유저의 성향이 비슷하다고 판단되었습니다.
심지어 SVD 이후 차원까지 축소했는데도 말이죠!

이렇듯 취향을 판단하면서, 데이터를 압축해야 할 경우에는 SVD가 유리하게 작동합니다.
또한, 차원을 낮추면서 근사하는 방식에는 SVD가 최적해를 도출한다고 증명이 되었습니다.

하지만, 압축한 데이터에 대해서는 해석할 수 없으며, 원래 행렬의 대부분의 값이 0으로 채워진 경우에는 SVD를 하면 오히려 원소의 개수가 늘어난다는 단점도 있습니다.