결정 트리 & 단순 베이즈 분류기

결정 트리

의사결정 지식을 트리의 형태로 표현한 것으로, 구성요소는 다음과 같습니다.

구성요소	역할
내부노드	비교 속성
간선(edge)	속성 값
단말노드	부류(class), 대표 값

이런 결정 트리를 학습하는 알고리즘의 종류에 대해 알아보도록 하겠습니다.

정보 이득(IG)

데이터로부터 결정 트리를 생성하는 알고리즘으로, 모든 데이터를 포함한 하나의 노드로 구성된 트리에서 시작하여, 반복적인 노드 분할 과정을 거치며 서브 트리를 만들어갑니다.

트리는 간단하게 표현될수록(depth가 낮을수록) 좋은데, 이를 달성하기 위해서는 분류력이 높은$^*$ 속성을 상위 노드에 배치하는 것이 좋습니다.
($^*$분류력이 높다: 분류된 결과들이 비슷한 부류일수록 분류력이 높음)

이 때, 분할 속성을 결정할 때, 분류력이 높음을 수치화할 수 있을까요?
이 척도로 엔트로피 개념이 사용됩니다.

엔트로피는 비동질(불순도) 정도의 척도로, 클수록 비동질적이라는 뜻입니다.
즉, 엔트로피가 작을수록 동질성이 크다는 의미인데, 정보량 측정 목적의 척도로 사용됩니다.

정보량(I) 및 정보 이득(IG)은 아래와 같이 수식화 할 수 있으며, 정보 이득이 클수록 엔트로피의 차이가 크다는 뜻이고, 이는 우수한 분할 속성으로 분할되었다는 의미입니다.

여기서 p는 부류별 확률이고, 위 수식을 해석하면 다음과 같습니다.
부모 엔트로피가 $I$이고, 자식 트리의 엔트로피 가중 평균이 $I_{res}$일 때, 그 차이가 커야 부모 노드(속성)을 잘 선택해서 분류했다는 뜻입니다.

예를 들어 이해해봅시다.

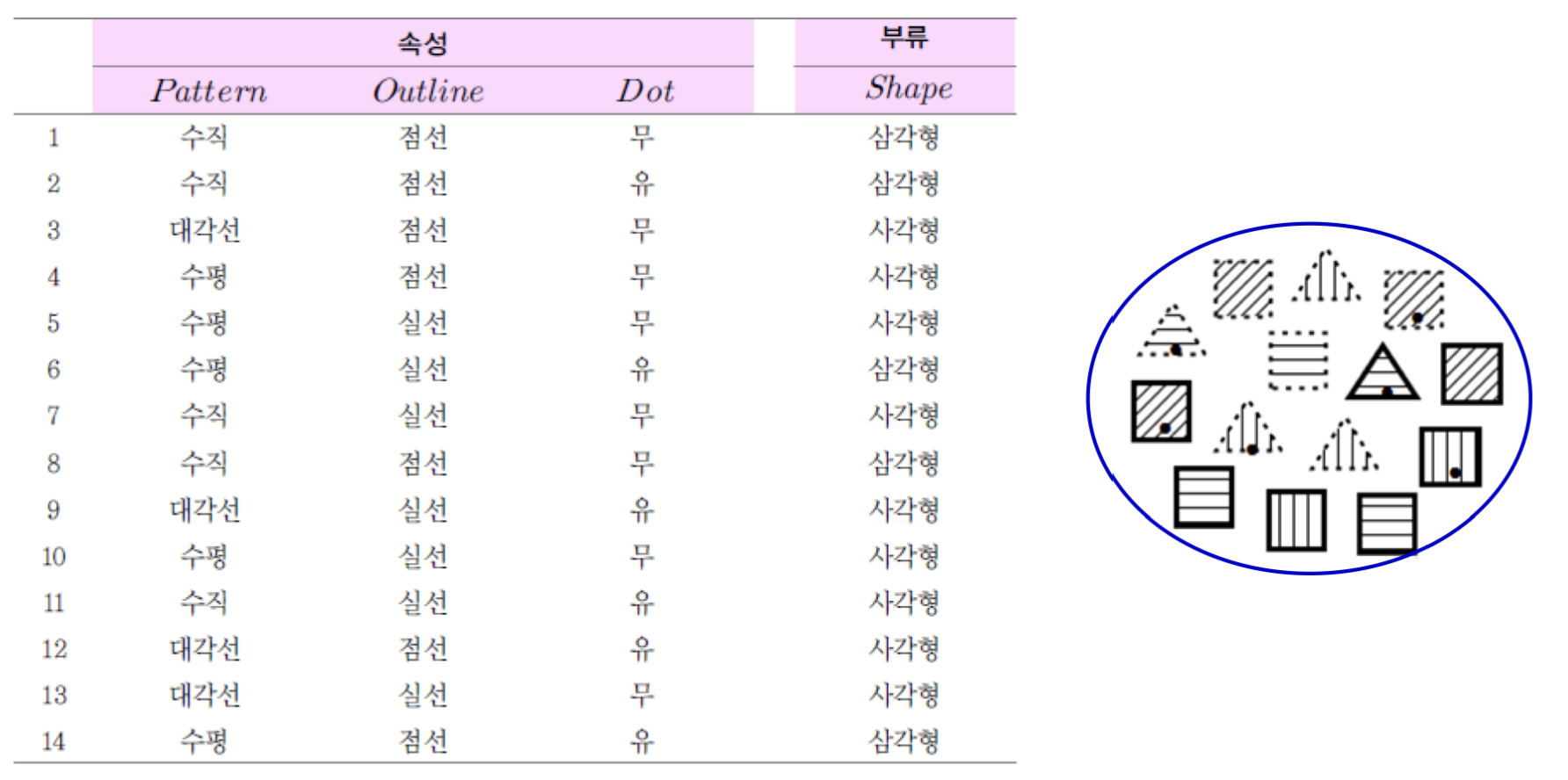
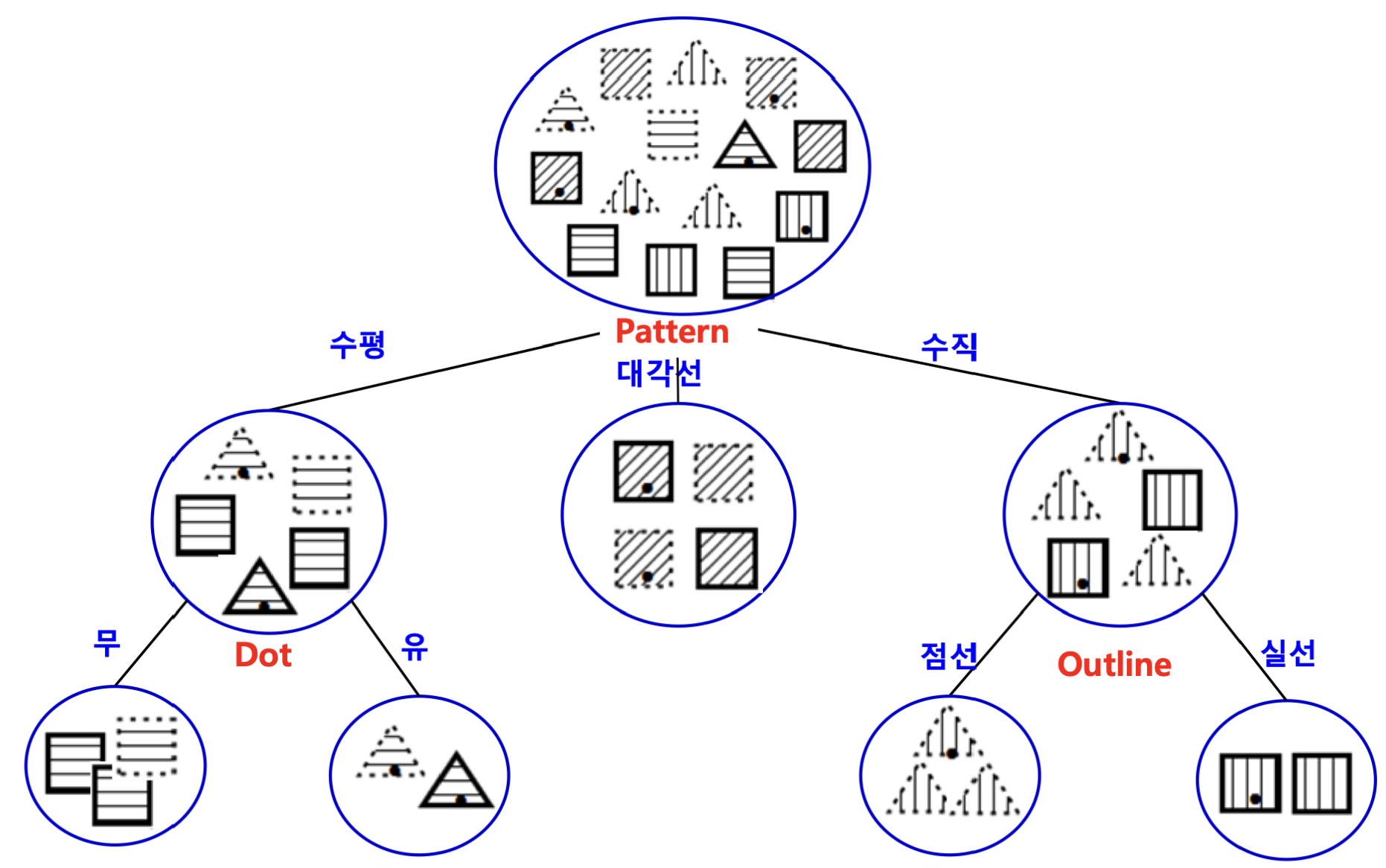
이런 데이터를 분류한다고 가정해봅시다.
이 때의 I는 아래와 같이 계산할 수 있습니다.

• Case 1: Pattern으로 분류

  

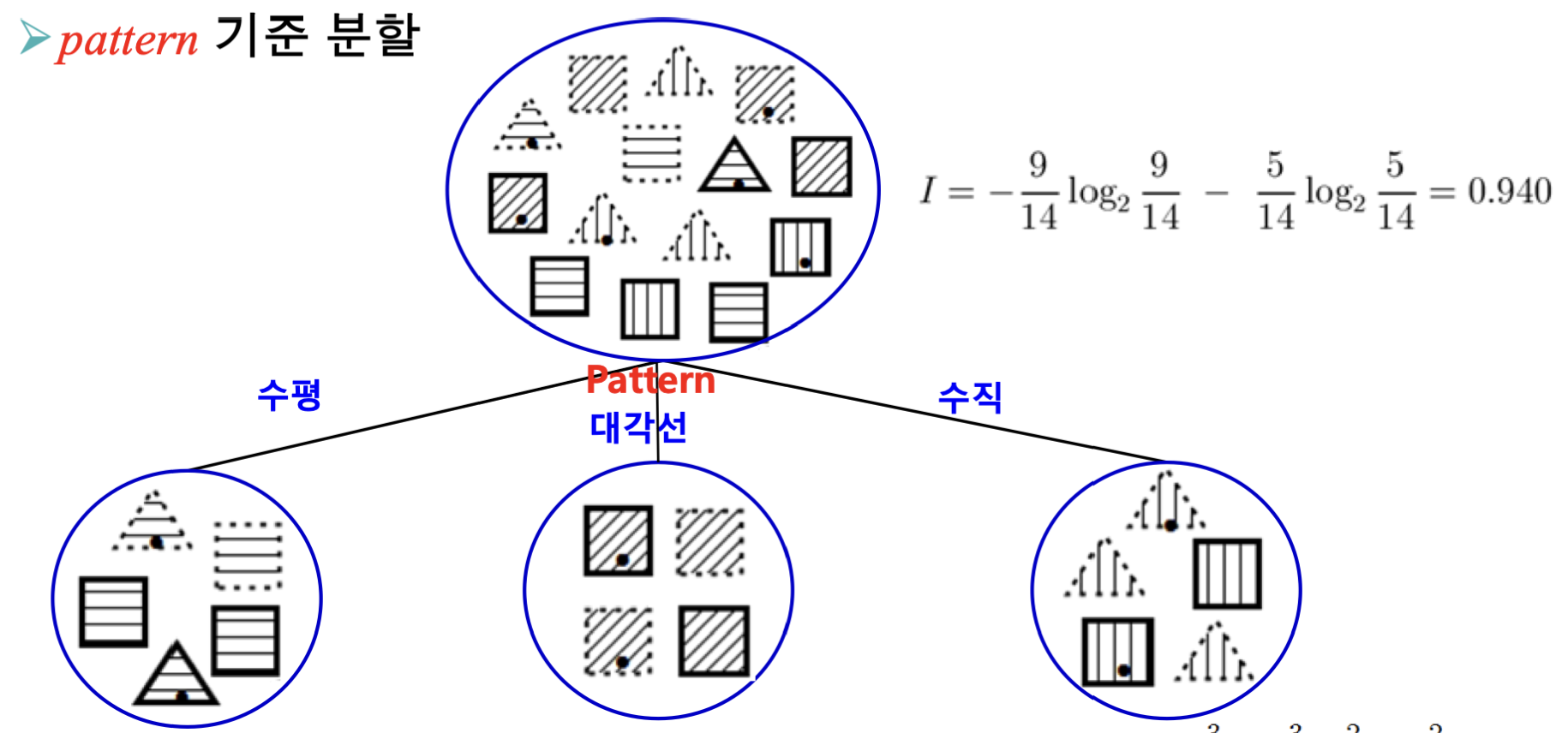
  Pattern이 수평, 대각선, 수직인지에 따라 분류할 경우 $I_{res}$를 계산해봅시다.

  $$I_{horizontal} = - \frac{2}{5}log_2\frac{2}{5} - \frac{3}{5}log_2\frac{3}{5} = 0.971 \\ {}\\ I_{digonal} = - \frac{0}{4}log_2\frac{0}{4} - \frac{4}{4}log_2\frac{4}{4} = 0 \\ {}\\ I_{vertical} = - \frac{3}{5}log_2\frac{3}{5} - \frac{2}{5}log_2\frac{2}{5} = 0.971 \\ {}\\ I_{res}(Pattern) = \frac{5}{14} \cdot 0.971 + \frac{4}{14} \cdot 0 + \frac{5}{14} \cdot 0.971 = 0.694$$

  즉, 분류 기준이 Pattern인 경우 IG = 0.246이 나옵니다.

• Case 2: Outline으로 분류

  

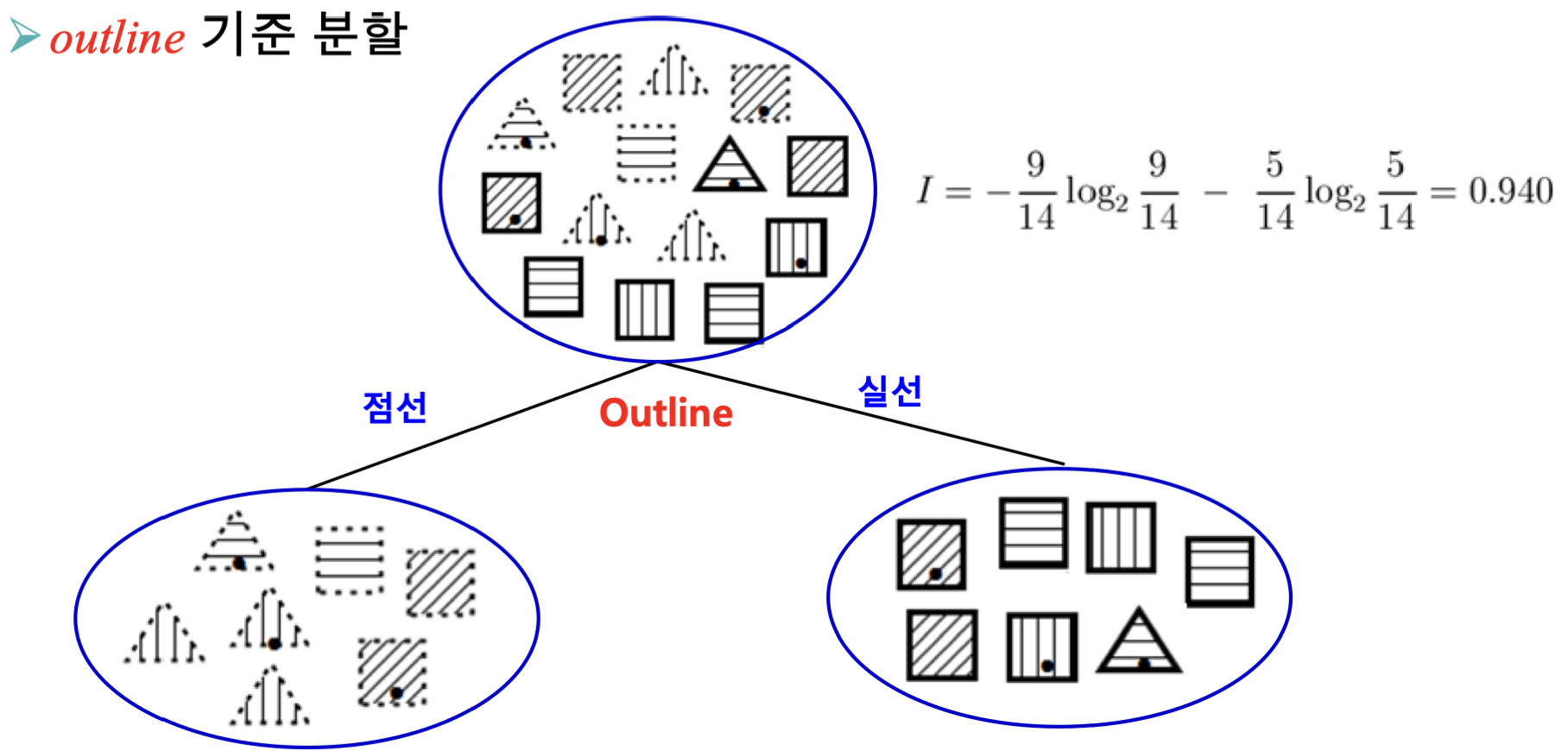
  Outline이 점선, 실선인지에 따라 분류할 경우 $I_{res}$를 계산해봅시다.

  $$I_{dashed} = - \frac{4}{7}log_2\frac{4}{7} - \frac{3}{7}log_2\frac{3}{7} = 0.985 \\ {}\\ I_{solid} = - \frac{1}{7}log_2\frac{1}{7} - \frac{6}{7}log_2\frac{6}{7} = 0.592 \\ {}\\ I_{res}(Outline) = \frac{7}{14} \cdot 0.985 + \frac{7}{14} \cdot 0.592 = 0.789$$

  즉, 분류 기준이 Outline인 경우 IG = 0.151이 나옵니다.

• Case 3: Dot으로 분류

  

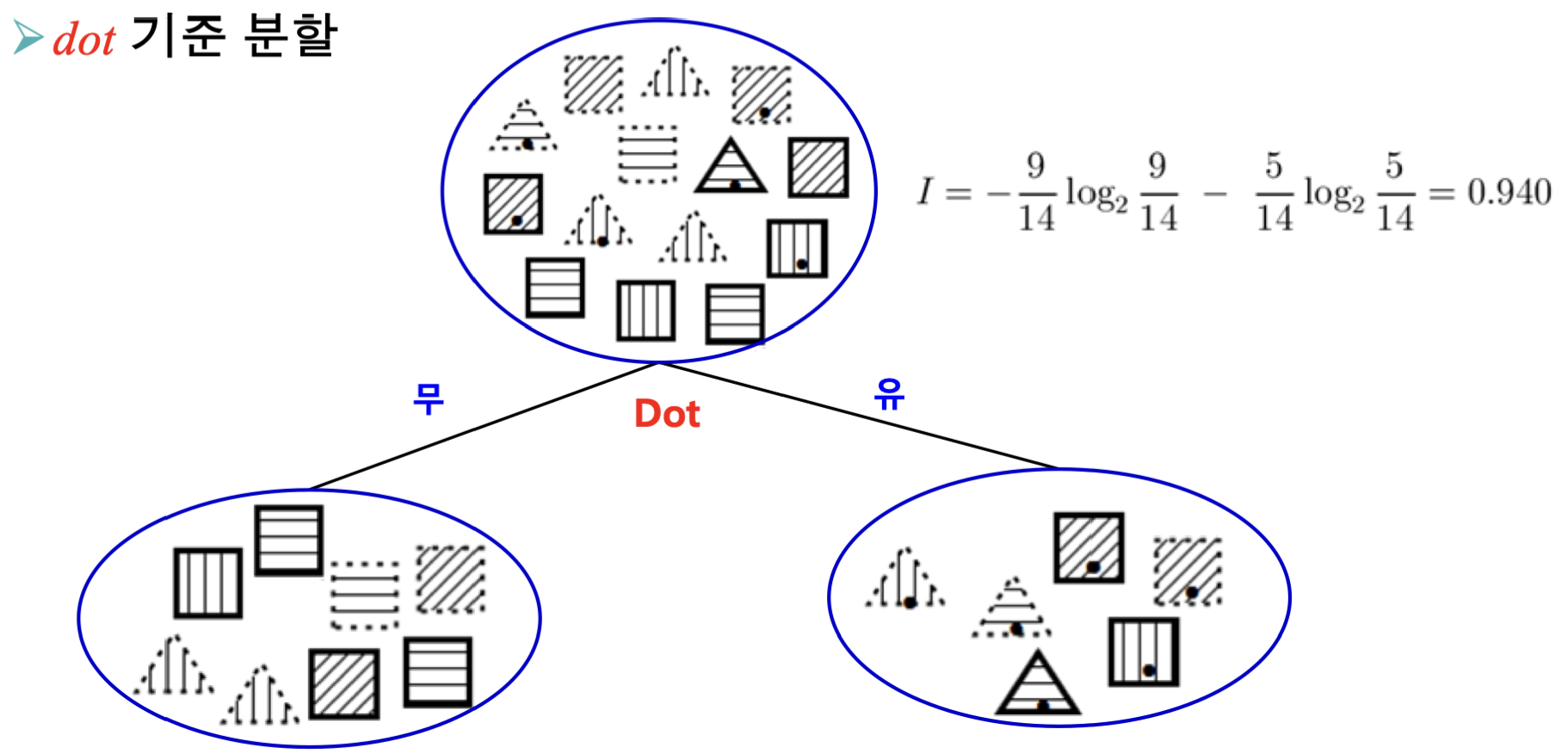
  Dot이 있는지, 없는지에 따라 분류할 경우 $I_{res}$를 계산해봅시다.

  $$I_{no} = - \frac{2}{8}log_2\frac{2}{8} - \frac{6}{8}log_2\frac{6}{8} = 0.811 \\ {}\\ I_{yes} = - \frac{3}{6}log_2\frac{3}{6} - \frac{3}{6}log_2\frac{3}{6} = 1 \\ {}\\ I_{res}(Dot) = \frac{8}{14} \cdot 0.811 + \frac{6}{14} \cdot 1 = 0.892$$

  즉, 분류 기준이 Dot인 경우 IG = 0.048이 나옵니다.

즉, 이 경우에는 첫번째 분류 기준으로 Pattern을 선택하는 것이 합리적입니다.
다음 분류기준을 선택할 때도 이와 동일한 방법으로 진행하면 되지만, 다음 분류기준을 Pattern으로 선택하는 것은 의미가 없기에 선택하지 않도록 주의합니다.

하지만, 정보 이득(IG) 척도의 단점 역시 존재합니다.
분류기준을 선택함에 있어 속성값이 많은 것을 선호한다는 것입니다.

예로 들어 학번같은 경우, 학번은 유니크하기 때문에 분류시 학번별로 노드가 만들어지고, 그에 따라 엔트로피가 아주 낮게 측정되어 학번이 분류기준으로 선택될 것입니다.
하지만, 학번으로 분류하는 것은 의미가 없죠.

뿐만 아니라, 학습 데이터 셋에 없던 속성값의 경우 분류가 불가능하다는 단점 또한 존재합니다.

정보 이득 비(IG Ratio)

속성값이 많은 것을 선호하는 문제를 해결하기 위한 개선된 알고리즘으로, 속성값이 많은 속성에 대한 불이익을 주는 방향으로 동작합니다.

여기서 I(A)는 고유 엔트로피로, 속성 A의 속성값을 부류로 간주하여 계산한 엔트로피를 의미합니다.
즉, 속성값이 많아질수록 엔트로피가 커지게 되므로, 학번을 분류기준으로 삼았을 때의 오류를 해결할 수 있습니다.

앞의 Case - Pattern을 예로 들어봅시다.

같은 방식으로 다른 분류기준에 대해 계산하면 다음과 같은 결과가 나옵니다.

분류속성	속성의 개수	IG	IG Ratio
Pattern	3	0.247	0.156
Outline	2	0.152	0.152
Dot	2	0.048	0.049

지니 이득(Gini Gain)

다른 분류 알고리즘으로 지니 지수를 사용하는 방법도 있습니다.

지니 지수는 위와 같이 수식화하며, 순도가 높을수록 낮은값이 나오게 됩니다.
이를 이용한 지니 지수 이득은 아래와 같습니다.

부모의 지니 지수에서 분류된 자식 트리의 지니 지수의 가중평균을 뺌으로서 구할 수 있습니다.
마찬가지로 앞의 Case - Pattern을 예로 들어봅시다.

같은 방식으로 다른 분류기준에 대해 계산하면 다음과 같은 결과가 나옵니다.

분류속성	IG	IG Ratio	Gini Gain
Pattern	0.247	0.156	0.058
Outline	0.152	0.152	0.046
Dot	0.048	0.049	0.015

회귀(Regression)

단말노드가 부류(class)가 아닌 수치(대표)값에 해당하는 경우 사용할 수 있는 분류법입니다.

표준편차 축소 SDR를 최대로 하는 속성을 선택하는게 졸으며, SDR은 아래와 같은 수식으로 표현 가능합니다.

---

단순 베이즈 분류기

결정 트리의 학습 알고리즘과 다르게 부류(class) 결정 지식을 조건부 확률로서 결정하는 분류기 입니다.

조건부 확률

$$P(c|x_1, x_2, ..., x_n)$$

베이즈 정리

$$P(c|x_1, x_2, ..., x_n) = \frac{P(x_1, x_2, ..., x_n|c)P(c)}{P(x_1, x_2, ..., x_n)} \\ {}\\ 사후확률 = \frac{가능도 \times 사전확률}{증거}$$

단순 베이즈 분류기는 베이즈 정리를 이용해서 분류를 하는데, 단순의 정의는 다음과 같습니다.

가능도가 조건부 독립이라고 가정

즉, 베이즈 정리를 다음과 같이 정의합니다.

예를 들어 이해해봅시다.

여기서 수직이며, 점선이고, 점이 없을 때 삼각형일 확률을 구해봅시다.