기계학습 - 지도학습
지도학습에서 사용되는 개념에 대해 알아봅니다.읽는데 9분 정도 걸려요.기계학습
사례들(examples)을 일반화하여 패턴 또는 모델을 추출하는 과정으로 학습 데이터를 잘 설명할 수 있는 패턴을 기계 스스로 학습하는 것을 유도하는 것이다.
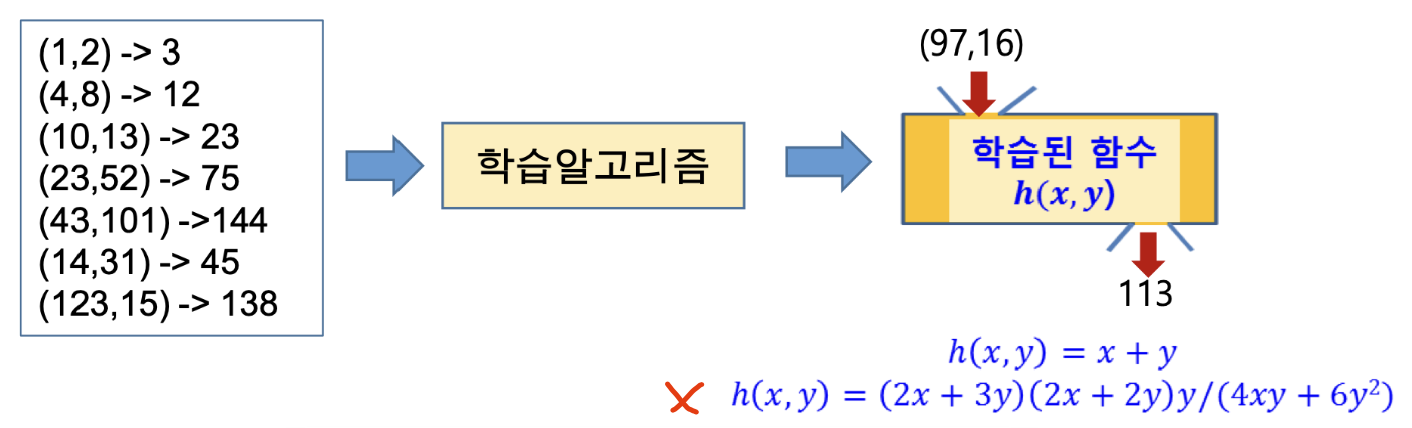
단, 오컴의 면도날(Occam's razor) 원리에 따라 가능하면 학습 결과가 간단한 형태로 표현되면 좋다.
기계학습의 종류에는 지도학습, 비지도학습, 반지도학습, 강화학습과 같은 방법이 있는데, 이번에는 지도학습에 대해서만 알아보자.
지도학습
주어진 학습 데이터 - (입력, 출력) 과 같은 데이터를 이용해서 학습하는 과정.
학습이 완료된 모델은 새로운 (입력) 이 있을 때 (출력) 을 유추할 수 있어야 한다.
출력이 불 연속적인 값이어야 한다면 데이터를 분류하는 방향으로 학습을 해야하고,
출력이 연속적인 값이어야 한다면 회귀하는 방향으로 학습을 해야한다.
분류 (Classification)
이상적인 분류기는 학습에 사용되지 않은 데이터에 대해서 분류를 잘 해야한다.
즉, 일반화의 능력이 좋은것이 이상적인 분류기이다.
데이터의 종류
- 학습 데이터
분류기를 학습하는데 사용하는 데이터 집합. - 테스트 데이터
학습된 모델의 성능을 평가하는데 사용하는 데이터 집합.
학습에 사용되지 않은 데이터여야 함. - 검증 데이터
학습 과정에서 학습을 중단할 시점을 결정하기 위해 사용하는 데이터 집합.
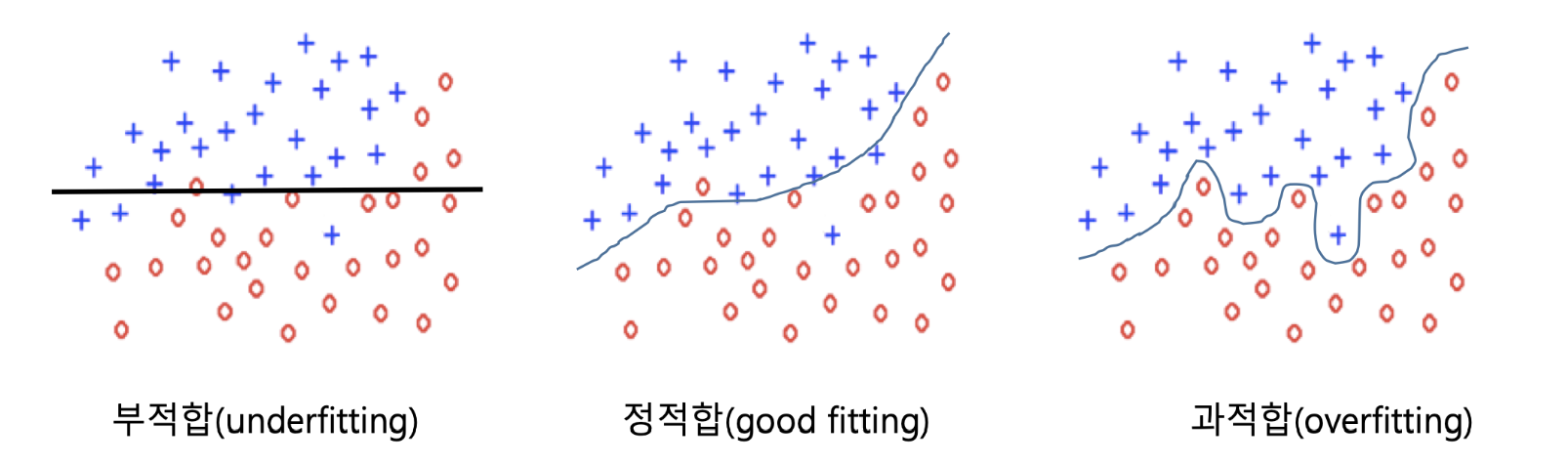
학습 데이터를 충분히 학습하지 않은 상태를 부적합 이라고 한다.
반대로학습 데이터에 대해 지나치게 잘 학습된 상태를 과적합 이라고 하는데, 학습되지 않은 데이터에 대해 좋지 못할 성능을 보일 가능성이 크다.
과적합을 회피하기 위해서 검증 데이터를 사용하게 된다.
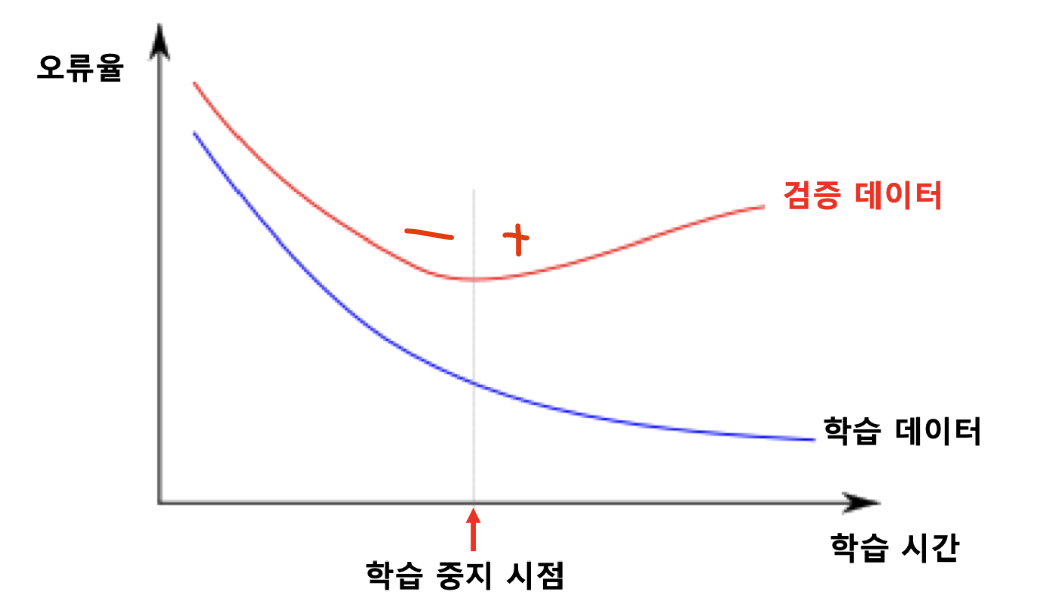
검증 데이터에 대한 오류가 증가하기 시작하면 학습 데이터에 대해 과적합이 일어나는 시점이기 때문에 이 때 학습을 중지하는 것이 좋다.
불균형 데이터 문제
특정 부류에 속하는 학습 데이터의 개수가 다른 부류에 비해 지나치게 많은 경우 정확도에 의한 성능 평가가 무의미해진다.
이게 무슨 의미냐면, A 부류의 데이터가 전체 데이터의 99%를 차지한다면, 분류기의 출력을 항상 A로 설정하는 경우 해당 학습 데이터에 대해 99%의 정확도를 보일 것이다.
하지만, 테스트 데이터에선 A/B가 각각 50% 비율로 들어있다면, 분류기의 정확도는 50%로 감소할 것이다.
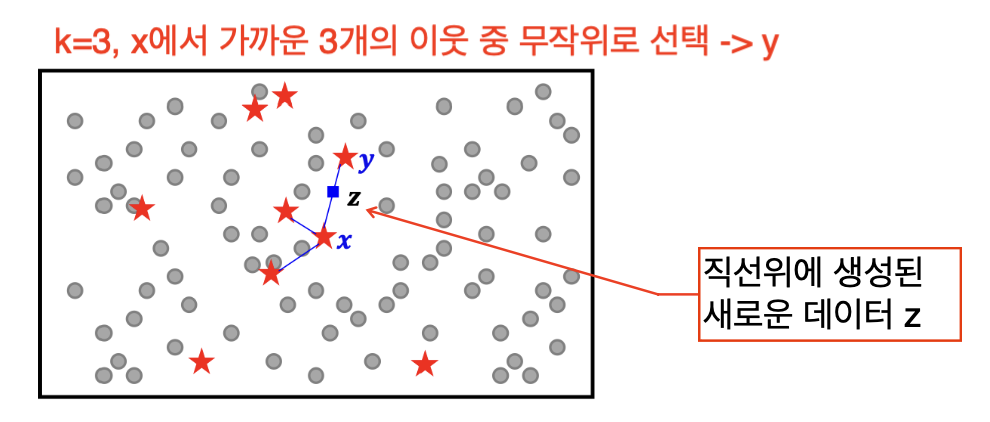
이런 경우 SMOTE 알고리즘을 이용해 어느정도 해결할 수 있다.
간단하게 설명하면 빈도가 낮은 학습 데이터의 k-근접 이웃을 이용해 새로운 데이터를 생성하여 빈도가 낮은 부류의 데이터 개수를 늘리는 알고리즘이다.
이진 분류기 성능 평가
이진 분류기는 두 개의 부류만을 갖는 데이터에 대한 분류기로 A/B 둘 중 하나로 분류하는 분류기이다.
이 분류기는 아래와 같은 예측-결과 표를 생성하는데,
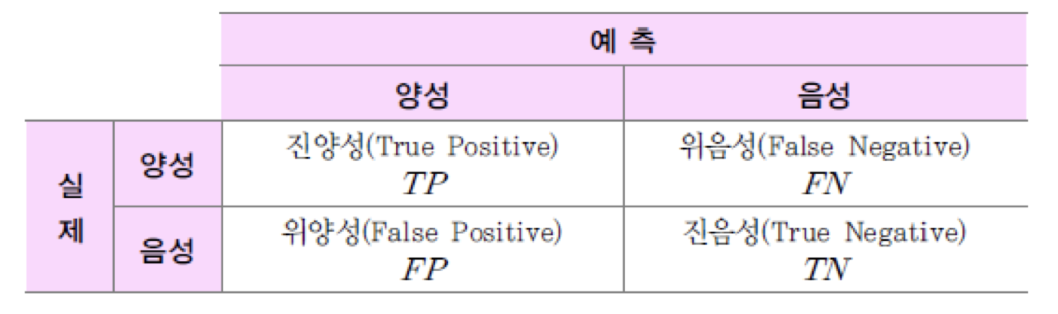
이것을 이용한 여러가지 지표로 성능을 평가한다.
-
민감도/재현율/진양성율
실제 양성일 때, 양성이라고 예측하는 확률이다.민감도 =
e.g. 불이났을 때, 불이 났다고 민감하게 알려주는 화재경보기
-
특이도/진음성률
실제 음성일 때, 음성이라고 예측하는 확률이다.특이도 =
e.g. 불이 안났을 때, 울리지 않는 화재경보기
-
정밀도
양성으로 예측을 했는데, 실제로 양성일 확률.정밀도 =
e.g. 화재경보기가 경보를 울렸는데, 실제로 불이 난 상황이었음
-
음성 예측도
음성으로 예측을 했는데, 실제로 음성일 확률.음성 예측도 =
e.g. 화재경보기가 안울렸는데, 실제로 불도나지 않았음
-
위양성율
1에서 특이도를 뺀 값.위양성율 = = 1 - 특이도
-
위발견율
1에서 정밀도를 뺀 값.위발견율 = = 1 - 정밀도
-
정확도
예측한대로 결과가 나올 확률.정확도 =
-
F1 측도
F1 = 2
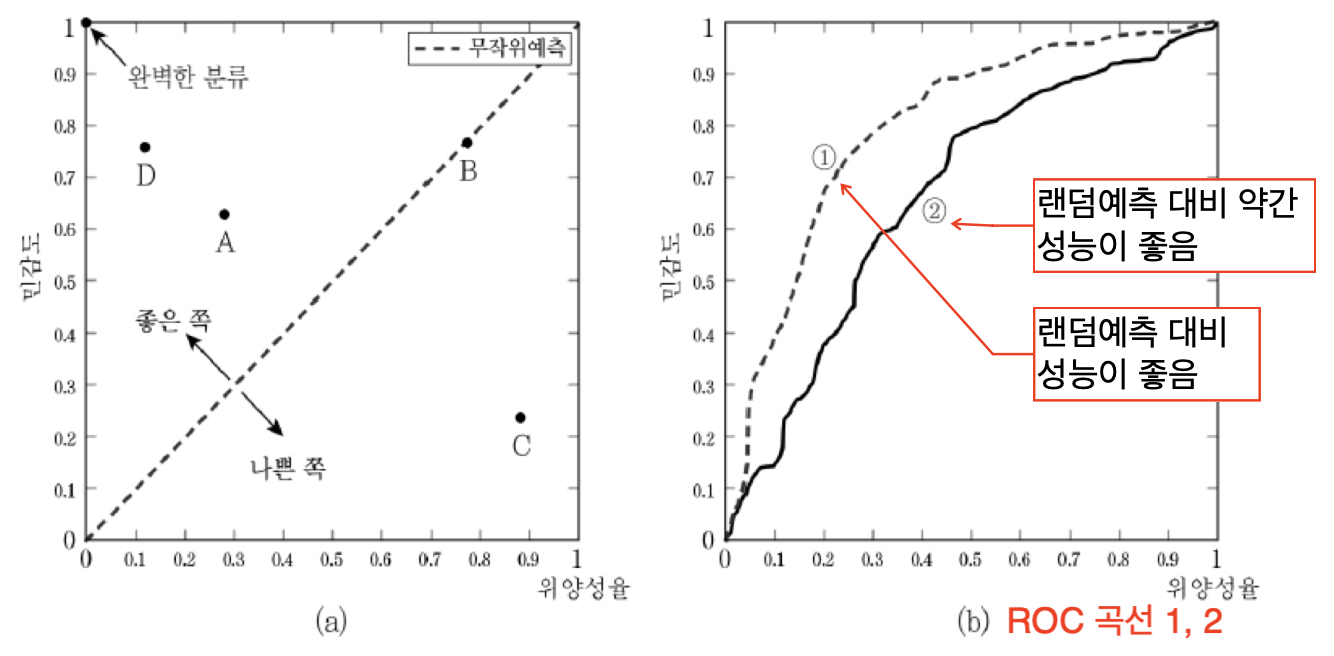
ROC 곡선
위양성률, 민감도 그래프로 ROC 곡선의 아래 면적, AUC(Area Under the Curve)가 클수록 바람직하게 분류한다는 뜻이다.
회귀 (Regression)
학습 데이터에 부합되는 출력값이 실수인 함수를 찾는 문제로, 앞에서 언급했 듯, 출력이 연속적이어야 하는 경우에 사용하는 방법이다.
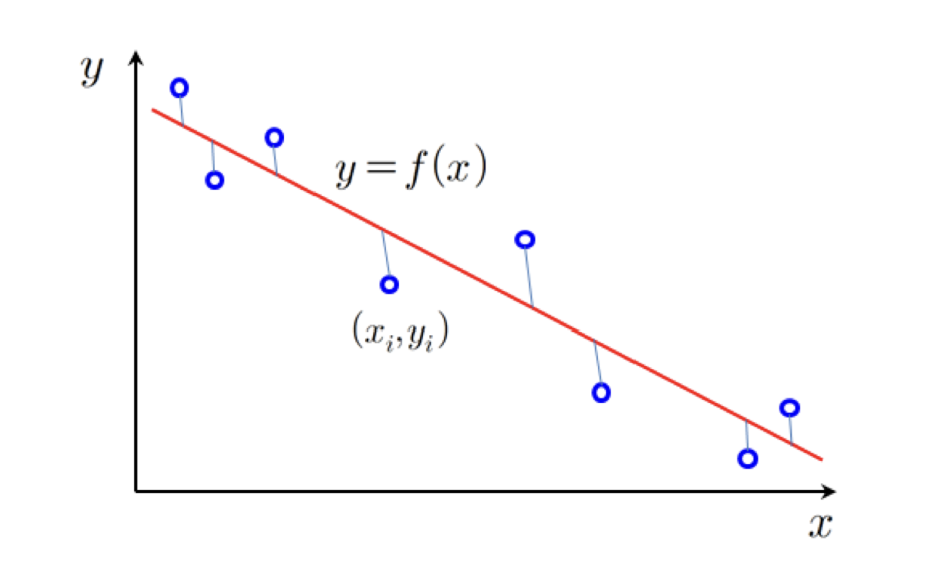
파란 점과 같은 학습 데이터가 주어졌을 떄, 해당 데이터를 가장 잘 설명하는 모델 를 찾기 위해서는 의 오차를 계산하는 함수 이 최소가 되도록 인자를 조정해야 한다.
회귀 성능 평가
학습 방향성과 같다.
테스트 데이터에 대한 오차값의 평균이 작을수록 좋다.
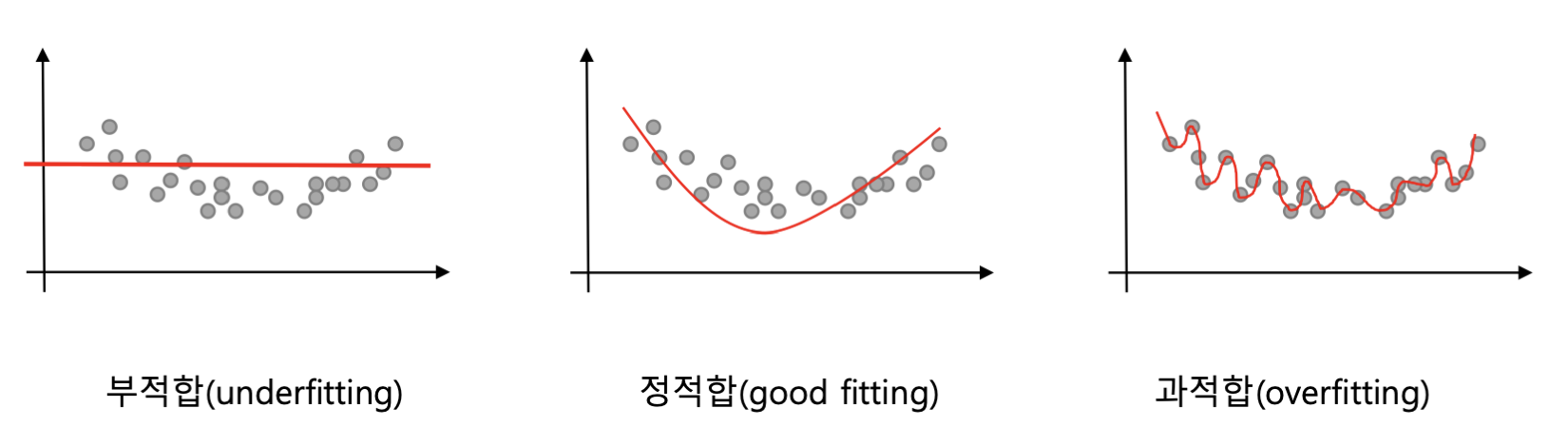
하지만 처음에 언급했 듯 과적합되는 현상은 피해야 한다.
이를 위해 모델의 복잡도를 일종의 패널티로써 성능 평가(목적함수)에 반영하여, 모델의 복잡도를 최소화 하는 방향으로 학습을 유도해야 한다.
로지스틱 회귀 (Logistic regression)
모델의 출력이 [0, 1] 사이의 값을 갖도록 조정해야 하는 경우 sigmoid 함수와 같은 로지스틱 함수를 이용해서 학습 데이터의 출력을 근사하는 방식을 사용할 수도 있다.
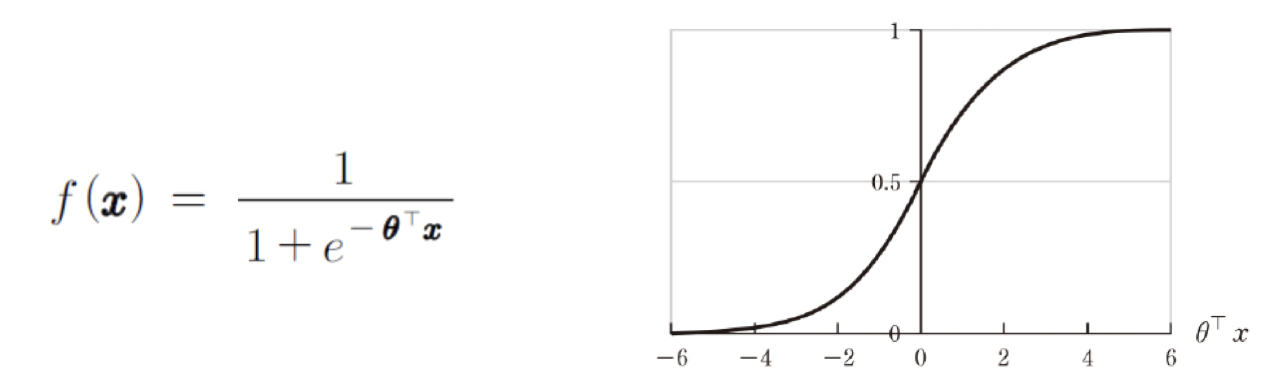
단, 이 때의 목적 함수는 교차 엔트로피(오차가 0~1 사이로 조정됨)가 적용된 함수를 사용해야 한다.
로지스틱 회귀는 경사 하강법을 사용하는 학습에서 자주 사용된다.