딥러닝 & CNN
딥러닝 및 CNN 방식의 종류와 모델들을 알아봅니다.읽는데 17분 정도 걸려요.딥러닝
일반적인 다수의 퍼셉트론을 이용해서 은닉층을 여럿 두었던 기존 신경망과 거의 유사하지만, 그 은닉층의 개수가 엄청 많은 신경망을 딥러닝 신경망이라고 합니다.
원시 신경망은 은닉층의 개수가 적었기에, 사람이 직접 특징을 추출해서 만든 특징 벡터를 이용해 학습을 시켰던 것에 반해,
딥러닝 신경망은 데이터 그 자체를 입력으로 주고, 특징 추출과 학습을 함께 수행할 수 있습니다.
즉, 스스로 데이터로부터 유의미한 특징을 추출하고 학습하기 때문에 성능이 우수합니다.
기울기 소멸 문제
단, 딥러닝시 문제가 있습니다.
컴퓨팅 파워가 많이 필요하단 것은 둘 째 치고, 학습하는 과정에서 역전파를 할 때, 역전파 하는 과정에서 전파될수록 기울기(gradient)가 점점 줄어들다가 소멸하는 문제가 있습니다.
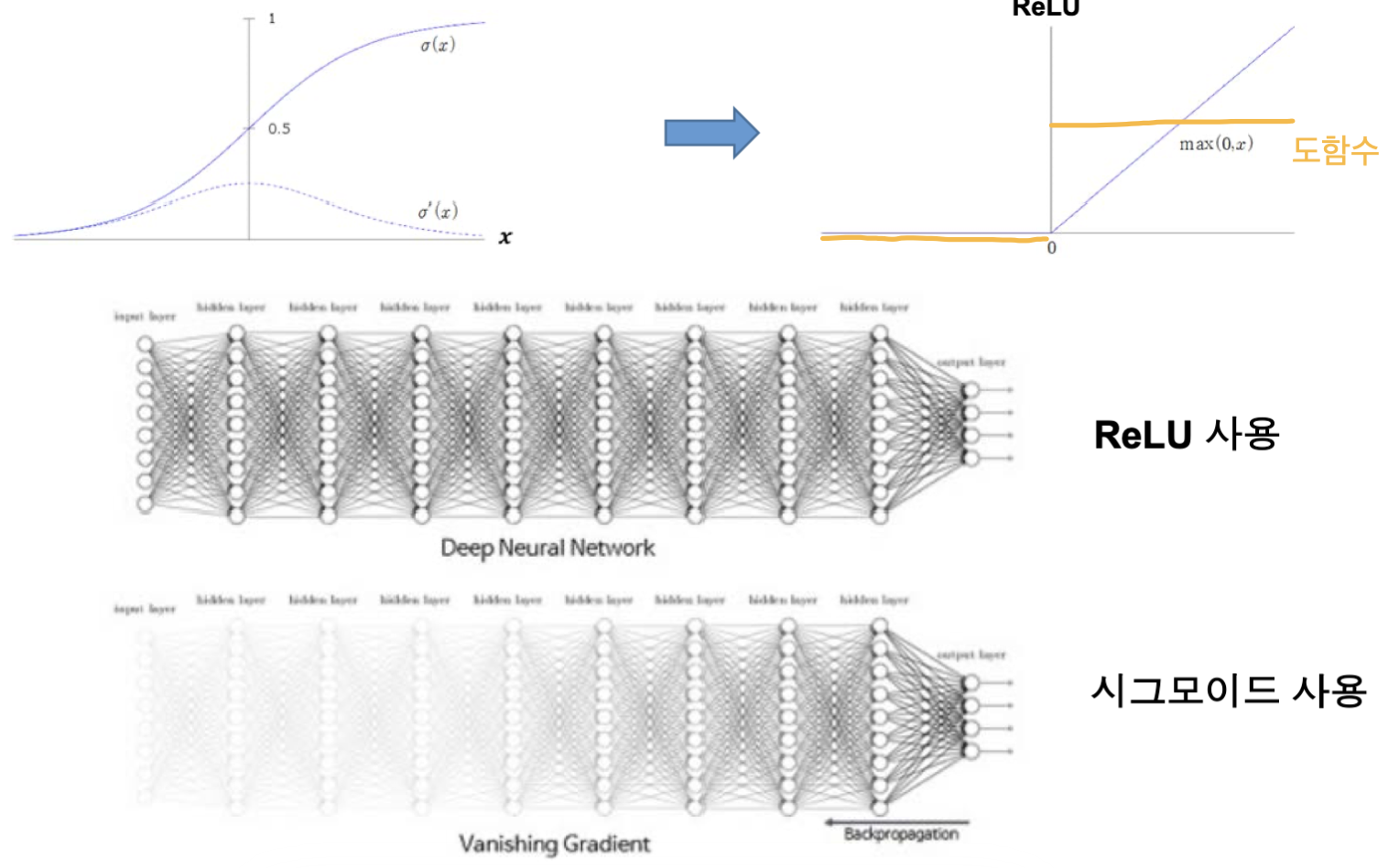
기울기 소멸 문제가 발생하는 이유는 sigmoid, typertangent와 같은 활성함수를 사용하기 때문에 발생하는 것인데, 이런 활성함수의 특징이 있습니다.
바로, 0에서 멀어질수록 도함수(기울기)의 값이 0에 가까워진다는 점입니다.
따라서 아무리 멀어져도 기울기가 0으로 수렴하지 않도록 ReLU 함수나 ReLU 파생 함수를 사용하곤 합니다.
가중치 초기화 문제
신경망을 학습하는 과정에서 경사하강법을 사용한다고 했었는데, 경사하강법의 문제가 있습니다.
바로 국소 최적해에 빠질 수 있다는 것입니다.
gradient의 반대 방향으로 이동하는 과정에서 더이상 움직이지 않는 지점까지 내려왔는데, 알고보니 그 지점보다 더 낮은 지점이 존재하는 것이죠.
즉, 학습에 있어, 초기에 가중치를 어떻게 초기화하느냐에 따라 학습 방향이 변하게 될 수 있다는 뜻입니다.
보통은 초기값으로 0에 가까운 무작위 값을 넣곤하는데, 균등 분포, Xavier 초기화, He 초기화 방법 등이 있습니다.
과적합 문제
학습을 너무 완벽하게 시켜도 문제입니다.
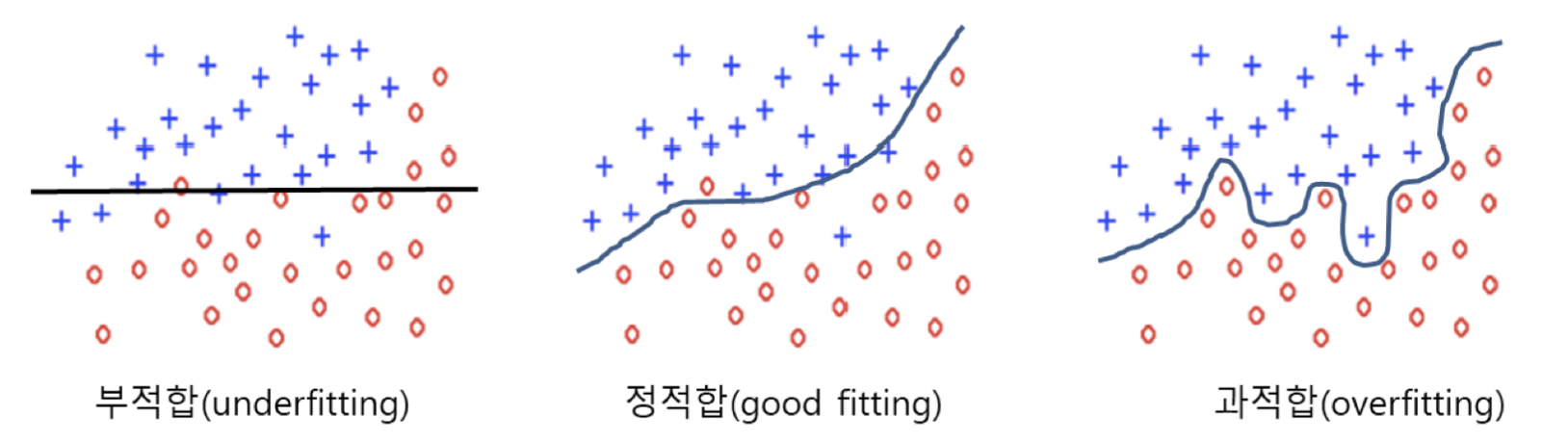
해당 모델은 학습 데이터를 완벽하게 분류할 수 있을 뿐, 테스트데이터에 대해서는 좋지 못한 성능을 보일 수 있기 때문입니다.
따라서 여러 과적합 완화 기법이 있습니다.
-
규제화 기법
오차함수에 error 뿐 만 아니라 모델 복잡도도 평가요소로 사용하는 방법입니다.
오차함수 = 오차 항 + 모델 복잡도 항
모델 복잡도는 가중치(weight)를 이용하여 정의할 수 있으며 아래와 같이 사용할 수 있습니다.
- L1-norm:
- L2-norm:
-
드롭아웃 기법
일정 확률로 노드들을 무작위로 선택해 선택된 노드 앞뒤로 연결된 가중치 연결선은 없는 것으로 간주하고 학습하는 기법입니다.
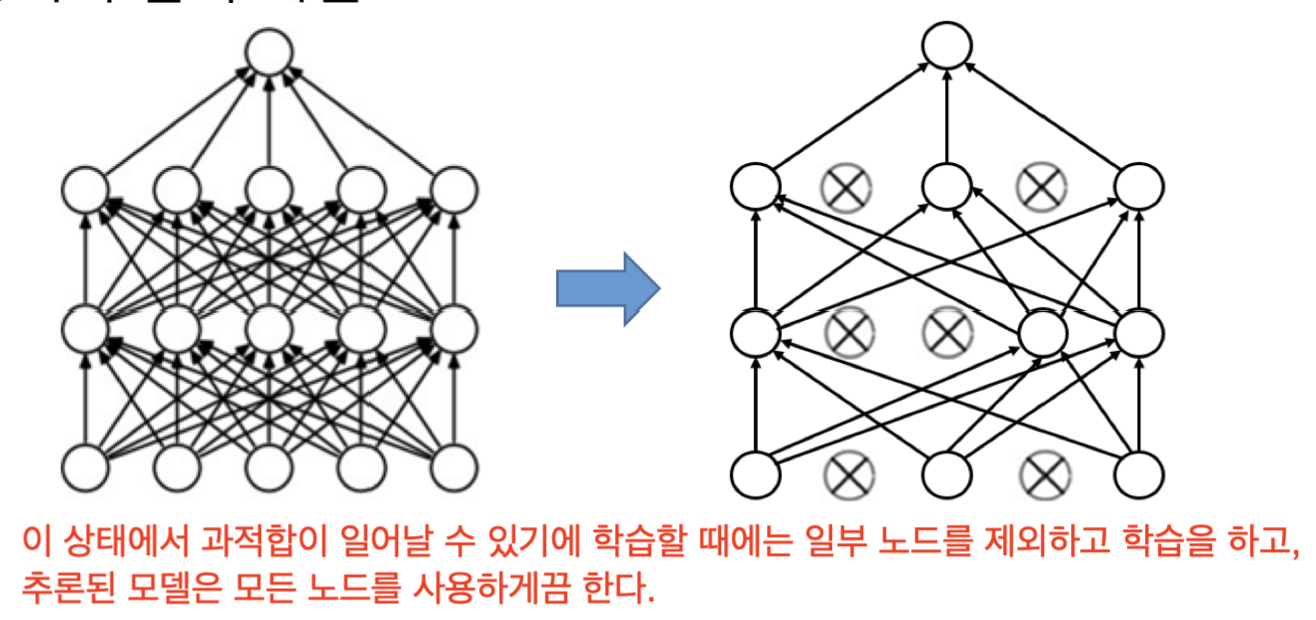
미니배치(mini-batch)나 학습주기(epoch)마다 드롭아웃할 노드를 선택하는데, 모든 노드는 한 번 이상은 특정 주기에 속해 학습되어야 합니다.
미니배치(mini-batch)전체 학습 데이터를 일정 크기의 데이터로 나누어 놓은 것으로, 학습 데이터가 큰 경우에 사용하는 것이 좋습니다.
단, 그레디언트를 계산할 때는 매 데이터마나 역전파해서 업데이트 하는 것이 아닌, 일정 수 이상의 데이터가 들어올 때 마다 평균을 계산해서 한 번에 업데이트 해야합니다.미니배치의 장점은 데이터에 포함된 오류에 대해 둔감하게 학습할 수 있기에 과적함 문제 완화에 도움이 됩니다.
-
배치 정규화
신경망의 각 층에서 미니배치의 각 데이터의 가중치 연산 결과의 분포를 정규화 하는 것으로, 간단하게 말하면 출력을 [-1, 1] 범위로 스케일링 하는 것입니다.
이게 도움이 되는 이유는 내부 공변량 이동 문제를 완화할 수 있기 때문인데요, 간단하게 설명하면 학습에 따라 가중치가 변하면 같은 학습 데이터에 대해 출력이 변하는 문제입니다.
하지만, 배치 정규화를 통해 출력을 정규화하면 같은 학습 데이터에 대해 시차가 있더라도 비슷한 출력을 내보낼 수 있게 되어 학습 효율이 올라갑니다.

연산 결과를 활성화 함수에 통과시키기 전에 배치 정규화 블록을 삽입하여 구현합니다.
컨볼루전 신경망 (CNN)
Convolution이란, 신경망에 컨볼루전을 처리하는 층이 추가된 딥러닝 신경망으로, 해당 컨볼루턴 층에서는 색상, 밝기, 에지 등등 특정 영역에 대한 특징을 추출하는 역할을 진행합니다.
(컴퓨터 비전의 그 컨볼루전임)
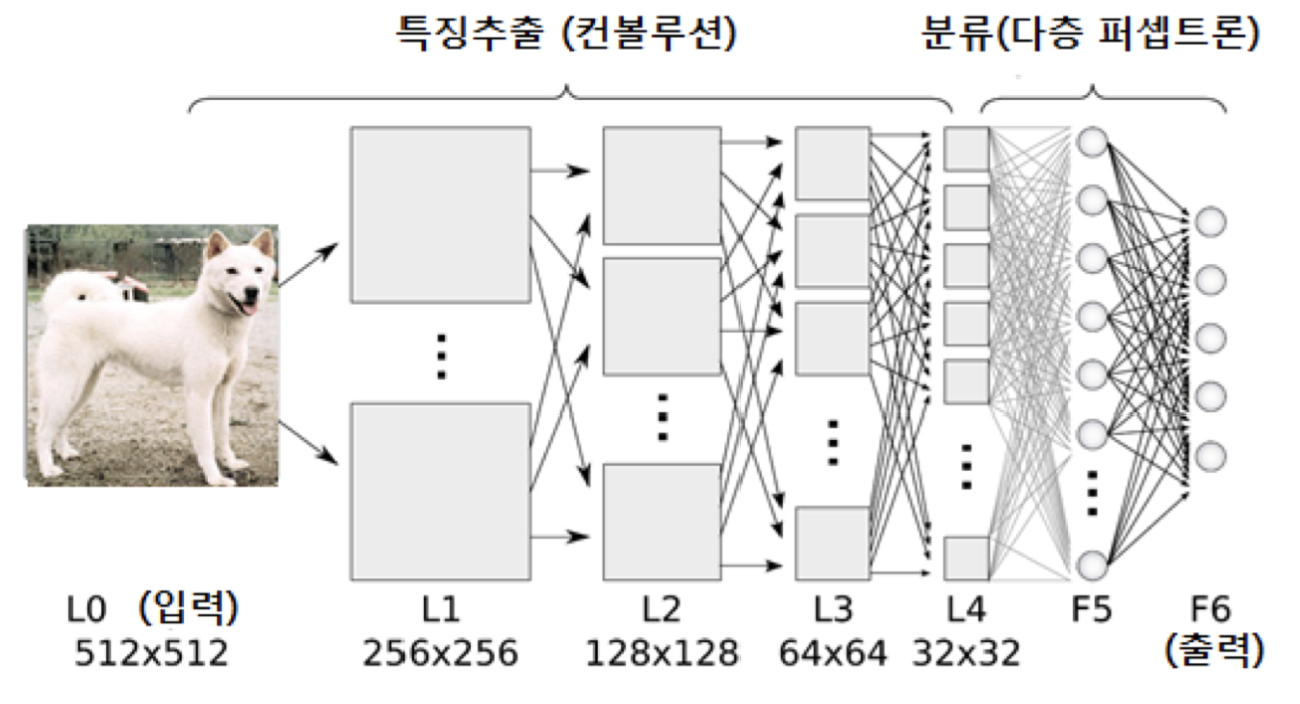
이런 컨볼루전은 여러개 두어 각 영역 특징들을 추출하고, 해당 특징을 이용해 딥러닝 신경망의 새로운 입력으로 사용해 의미있는 정보로 변환되게 됩니다.
컨볼루전
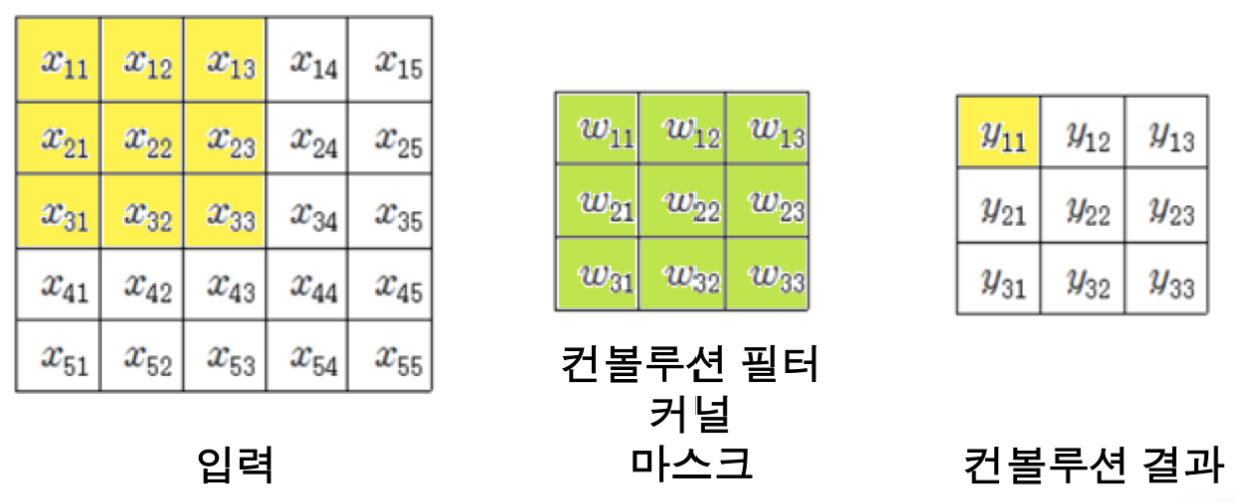
컴퓨터 비전과 비슷하게 일정 영역의 값에 가중치를 적용하여 하나의 값을 얻는 과정입니다.
단, 여기에 threshold에 해당하는 bias 도 더해진다는 차이점이 있습니다.
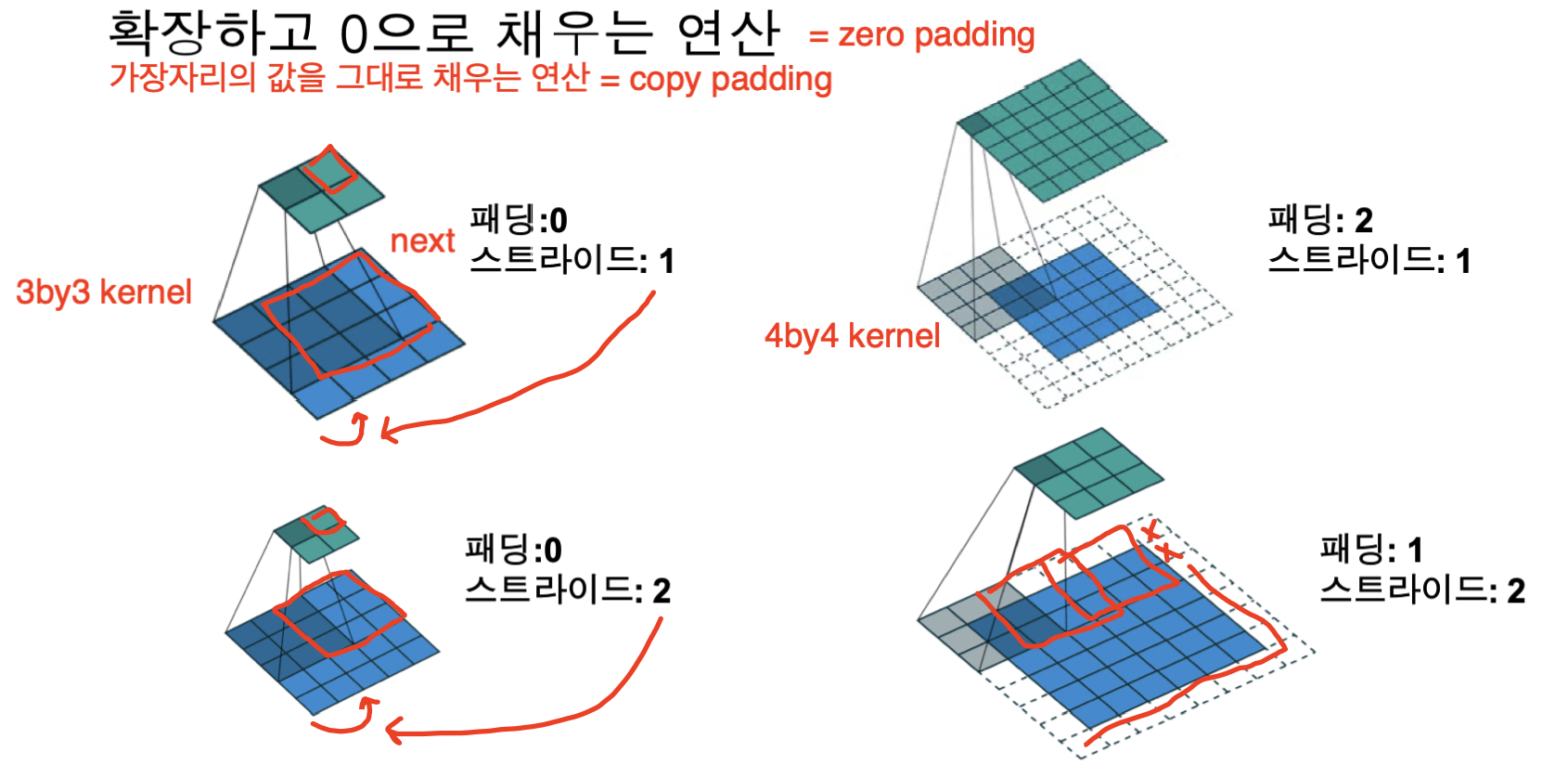
컨볼루전시 padding과 stride 요소에 따라 연산이 조금 달라지게 되는데요,
피연산 배열을 확장하는 것을 padding, 커널의 이동거리를 stride라고 합니다.
특징지도
컨볼루전 필터의 적용 결과로 만들어지는 2차원 행렬(N차원 배열)을 feature map 이라고 합니다.
단순히 컨볼루전의 연산 결과라고 생각해도 됩니다.
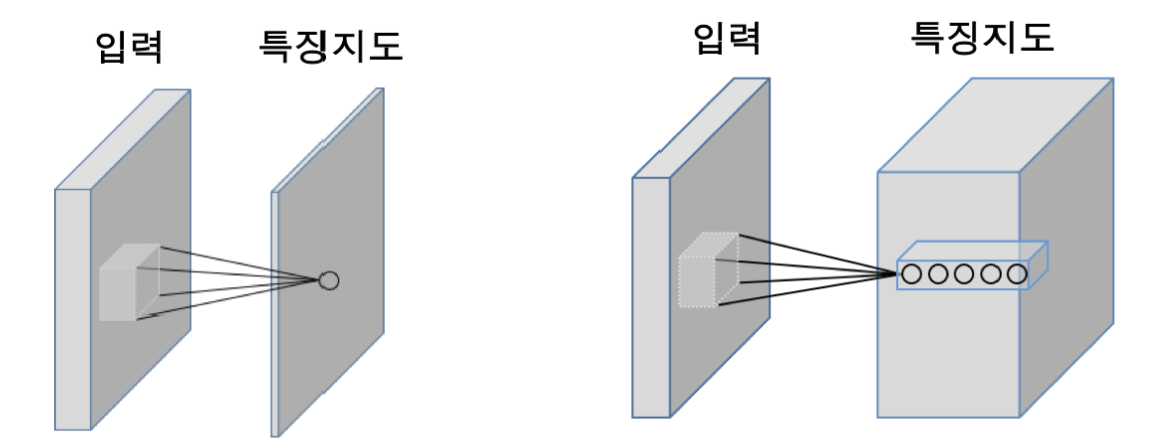
k개의 커널을 컨볼루전하면 k개의 2차원 특징지도가 만들어집니다.
커널은 RGB, 모서리, 경계선, 주파수 등등 필요한 정보를 추출할 수 있는 커널을 사용할 수 있습니다.
풀링
일정 크기의 블록을 통합하여 하나의 대푯값으로 대체하는 연산을 pooling 이라고 합니다.
특징지도의 크기를 축소함으로서 다음 단계에서 사용할 메모리 크기와 연산량을 감소하는데 사용되며,
특정 영역내의 특징을 결합하거나, 위치변화에 둔감한 특정을 선택하는 효과를 얻을 수 있습니다.
풀링 방식의 종류에 대해 알아봅시다.
-
최댓값 풀링
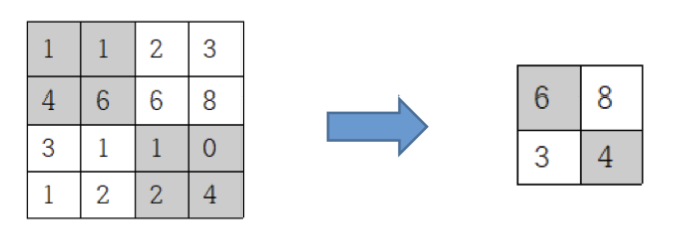
지정된 블록 내의 원소 중에서 최대값을 대푯값으로 선택하는 풀링입니다.
-
평균값 풀링

지정된 블록 내의 원소의 평균값을 대푯값으로 선택하는 풀링입니다.
-
확률적 풀링
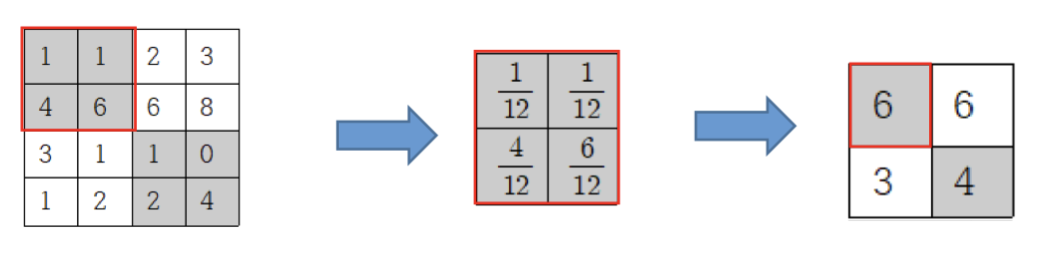
지정된 블록 내의 원소의 값의 크기에 비례하는 확률로 선택하는 풀링힙니다.
학습시에는 확률적으로 학습하기에 랜덤성이 부여되는 장점이 있고,
추론시에는 확률에 가중치를 둔 평균으로 구하는 방식으로 동작합니다.
CNN 구조
특징을 추출하는 컨볼루전 부분과 추출된 특징을 사용하여 분류, 회귀하는 다층 퍼셉트론 부분으로 구분됩니다.
컨볼루전 부분은 보통 아래의 층드로 구성된 블록들을 여럿 반복하여 배치합니다.
- Conv: 컨볼루전 연산
- ReLU: 활성화 함수
- Pool: 풀링
ReLU, Pool은 둘 다 쓰거나 둘 중 하나만 사용할 수도 있습니다.
다층 퍼셉트론 부분은 전 방향 연결되어있기에 FC(Fully Connected) 로 표현하며, 마지막 층은 출력을 정규화하기 위해 SM(SoftMax) 층을 둡니다.
이에 대한 예시는 다음과 같습니다.
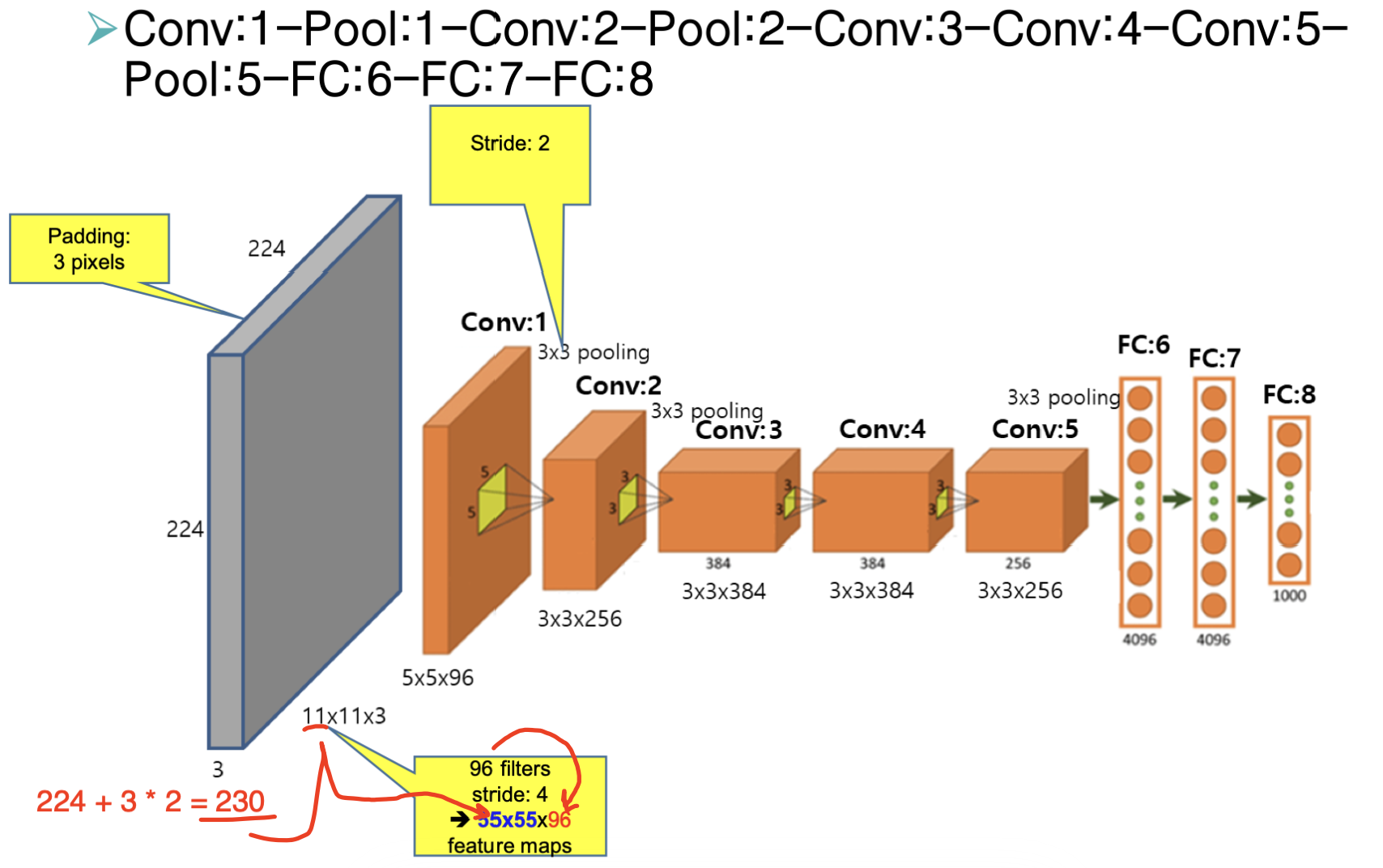
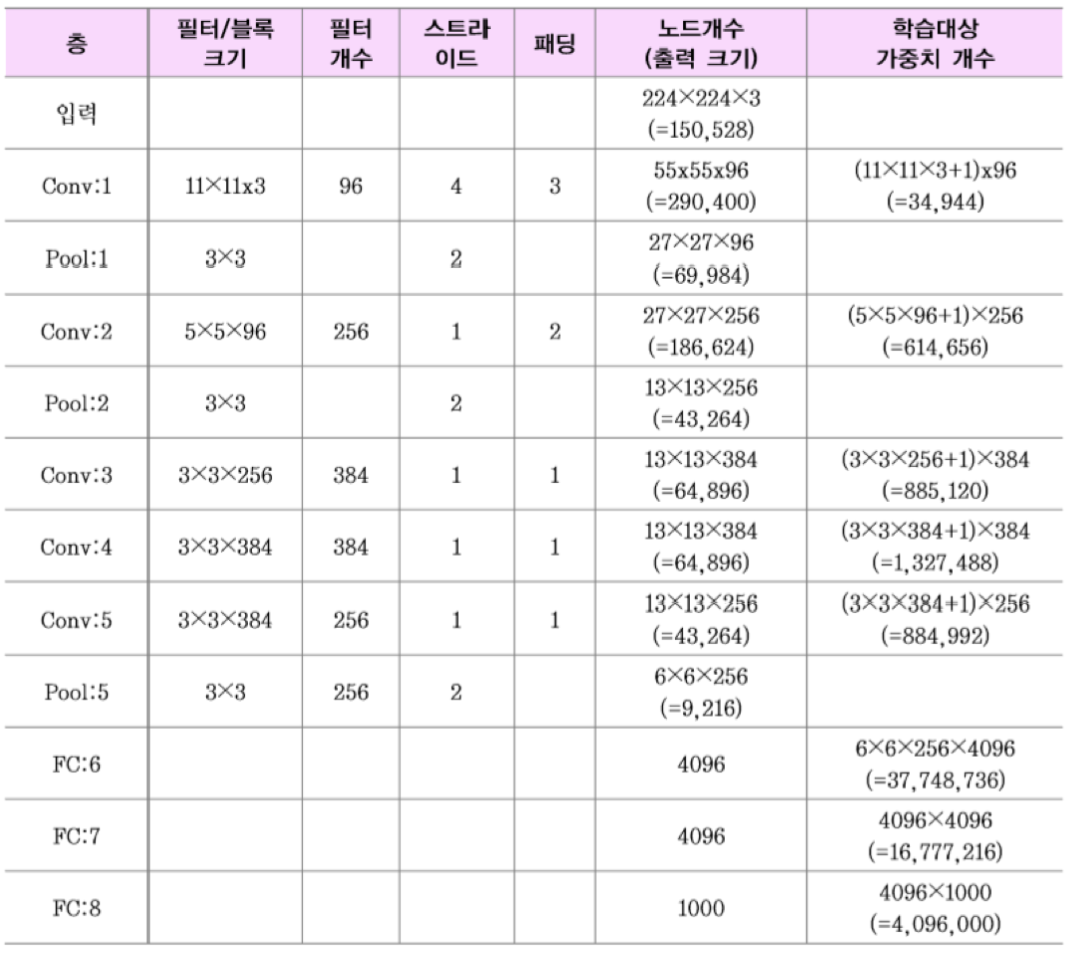
Pool을 제외하고는 가중치 연산이 필요합니다.
노드는 Conv에서 많은 경향이 있고, 가중치는 FC에서 많은 경향이 있습니다.
CNN 학습
CNN의 학습 방법은 여러 방법이 있지만, 제가 수식을 이해못한 관계로(...) 종류와 특징만 기술하도록 하겠습니다.
-
경사 하강법
그레디언트의 반대방향으로 학습률() 만큼의 보폭으로 이동하는 방식입니다. -
모멘텀을 고려한 경사 하강법
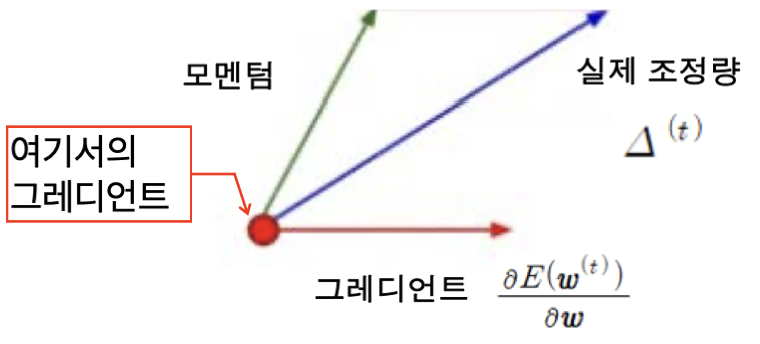
이전 그레디언트의 누적값을 반영하여 이동하는 방식입니다.
-
NAG
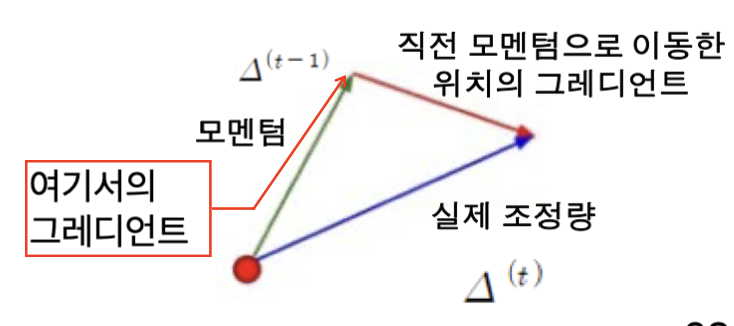
직전 모멘텀으로 이동한 위치에서의 그레디언트로 이동하는 방식입니다.
-
AdaGrad
가중치별로 별도의 학습률()을 적용하는 방식입니다.
예로 들어 x축보다 y축의 움직임이 크다면, y축에는 낮은 학습률을 적용하는 방식입니다. -
AdaDelta
AdaGrad의 변형으로 과거 그레디언트의 영향을 점점 줄이는 방식입니다. -
RMSprop
-
ADAM (best?)
CNN 모델 종류
전부 깊이 다뤄보지는 않고, ILSVRC 대회에서 좋은 성적을 거둔 모델 중 새로운 방식을 적용한 사례에 대해서만 알아봅시다.
LeNet
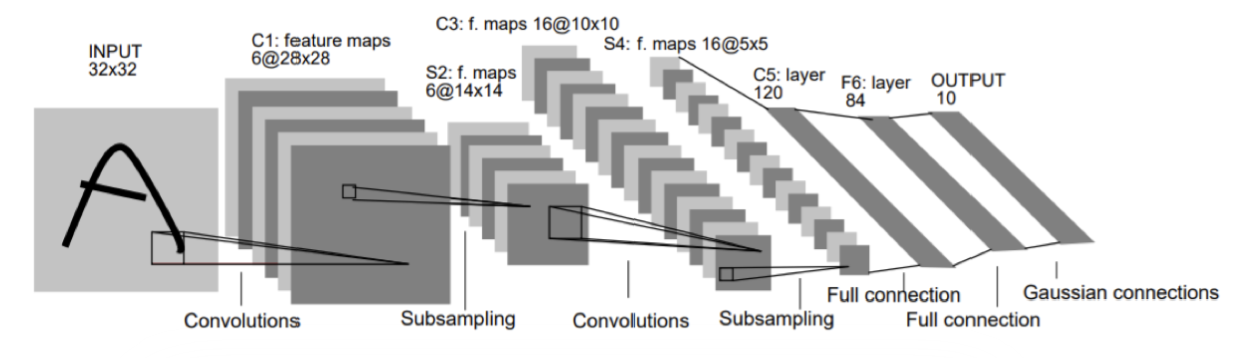
- 대회에서 최초로 컨볼루전을 사용
AlexNet
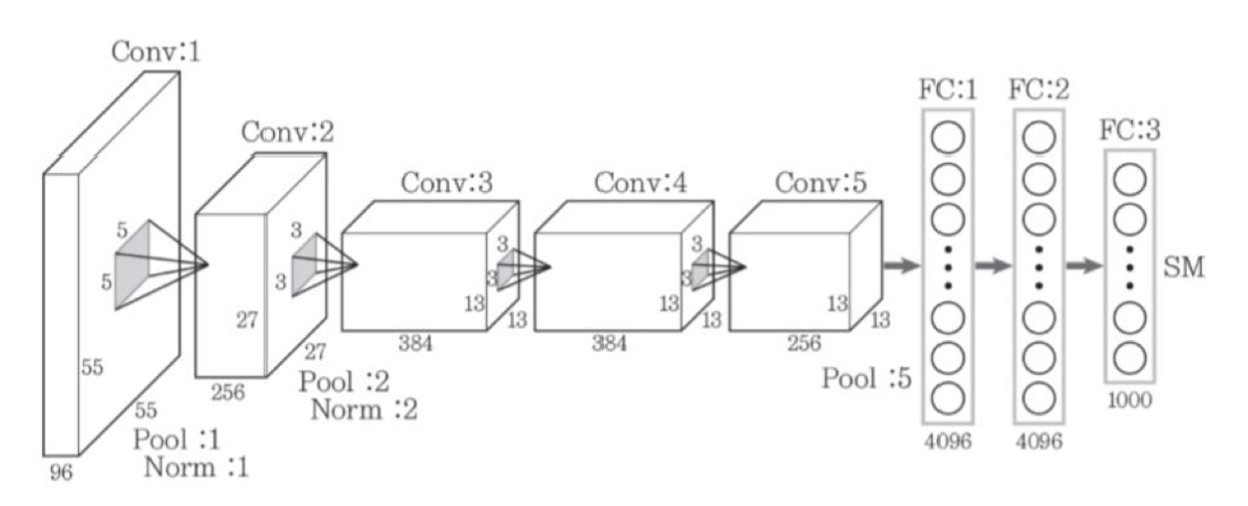
- 대회에서 최초로 ReLU 함수를 사용
- FC층에 드롭아웃 기법 적용
- 최댓값 풀링 사용
VGGNet
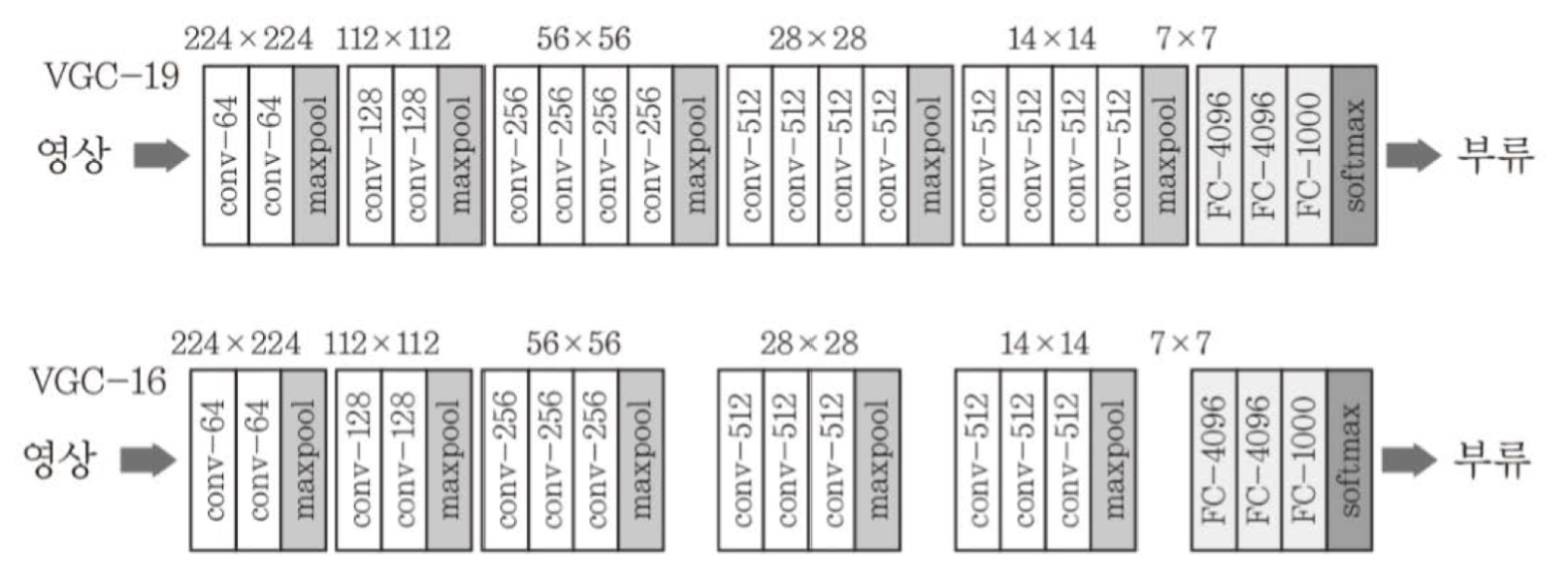
- 모든 컨볼루전 층에서 3by3 필터를 사용
3by3을 2번 적용하면 5by5를 적용한 효과를 낼 수 있고, 3번 적용하면 7by7을 적용한 효과를 낼 수 있습니다.
여기서 작은 필터를 여러번 사용하는게 큰 필터 한 번을 사용하는 것 보다 좋은 효과를 얻을 수 있었는데요,
그 이유는 가중치 개수가 적어지는 효과도 있고, 컨볼루전만 하면 선형 변환이라 중간에 ReLU 같은 비선형 변환을 사용해야 하는데, ReLU를 많이 사용할수록 복잡한 결정 경계를 표현할 수 있게되기 때문입니다.
GoogleNet
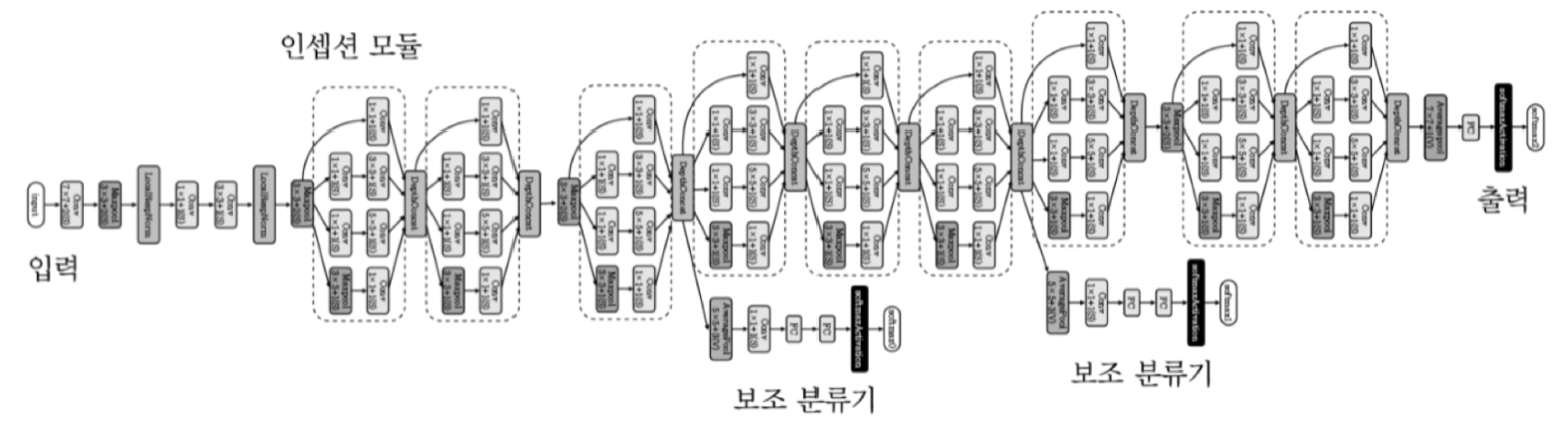
- 인셉션 모듈 사용
- 1by1 컨볼루전 사용
- FC층 단 1개 사용
- 보조 분류기 사용해 기울기 소멸 문제 완화
인셉션 모듈
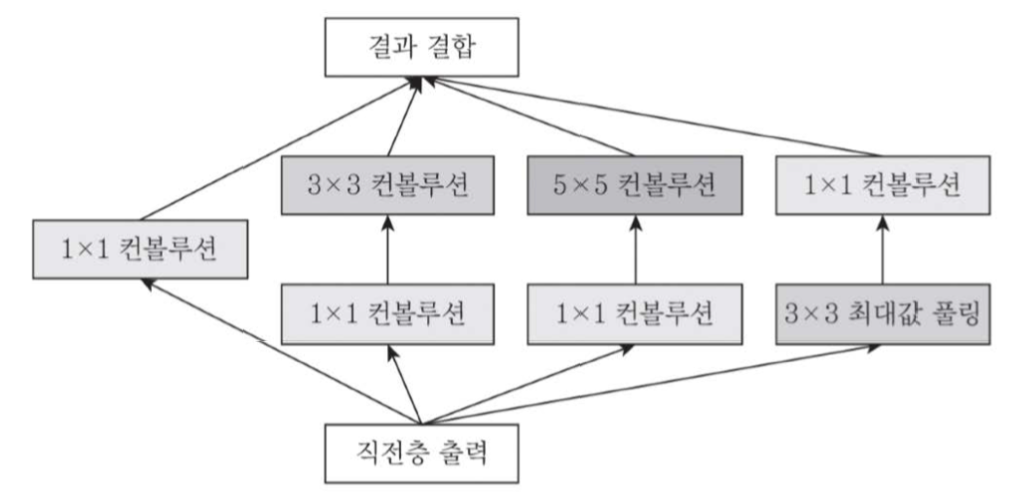
특징을 동시에 추출할 수 있습니다.
1by1 컨볼루전
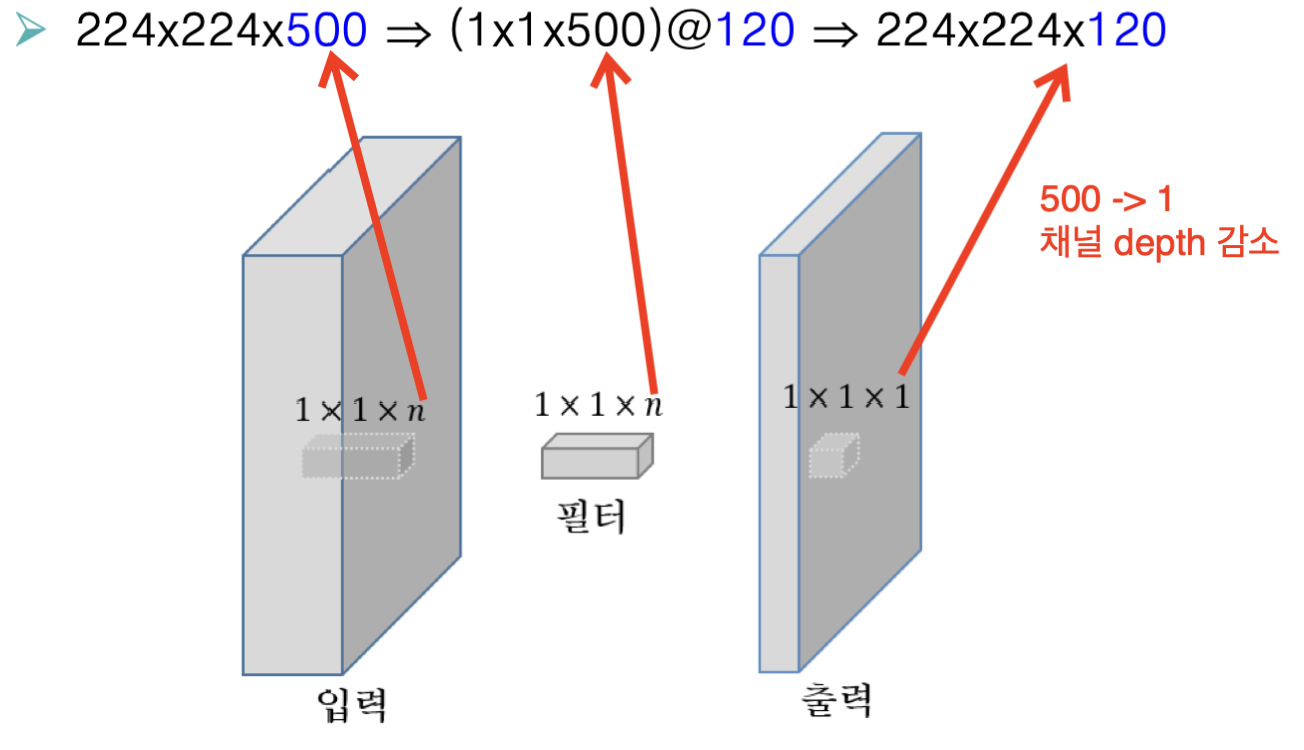
특징지도를 압축할 수 있습니다.
ResNet
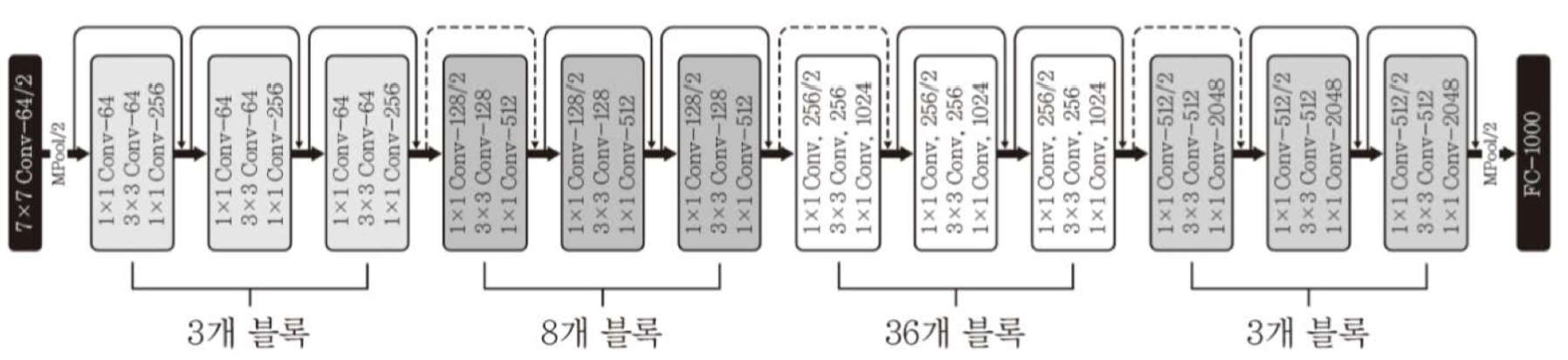
- 잔차 모듈 사용
잔차 모듈
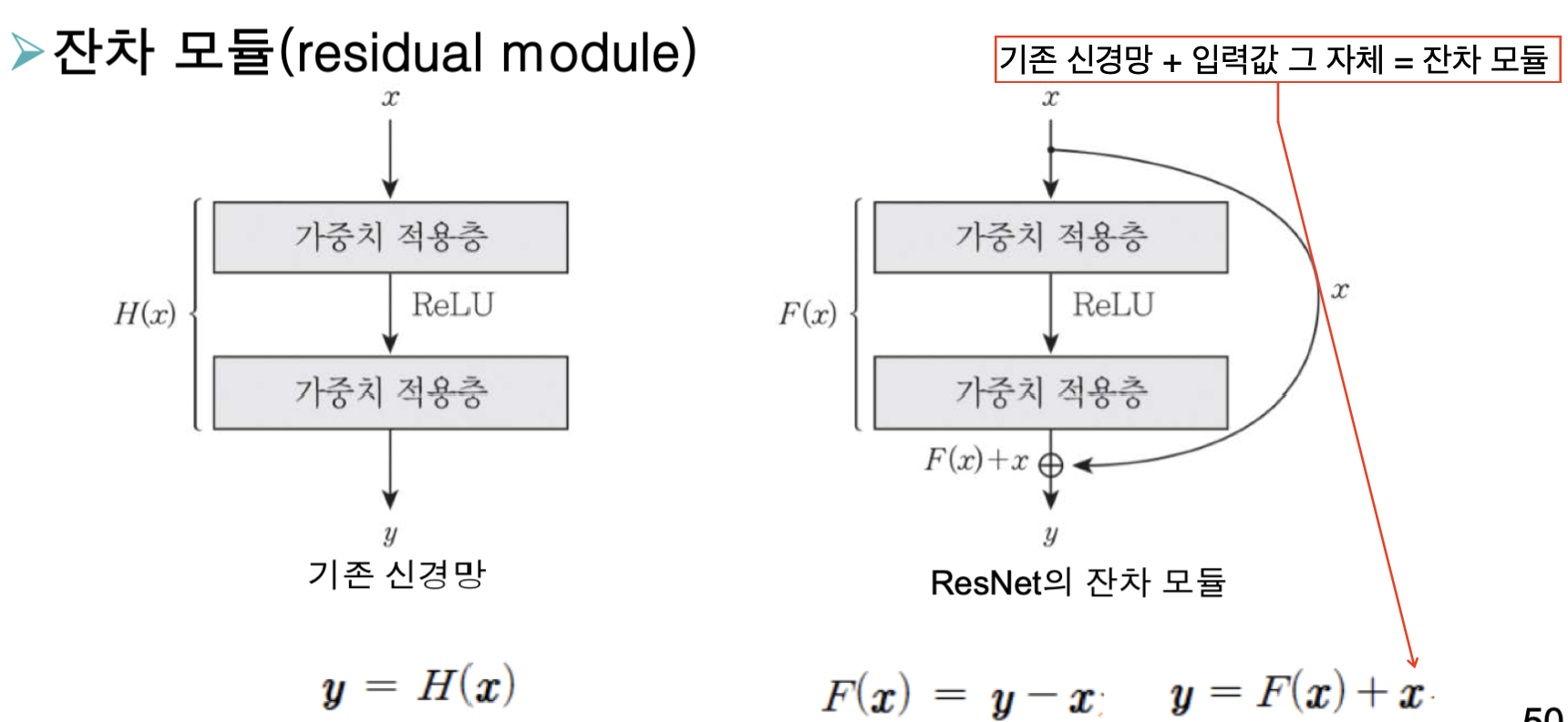
입력값을 그대로 넘기는 과정이 추가된 모듈로 이를 이용하면 기울기 소멸 문제를 완화할 수 있습니다.
뿐만 아니라, 작은 변화에도 민감하며, 다양한 경로를 통해 복합적인 특징을 추출할 수도 있습니다.
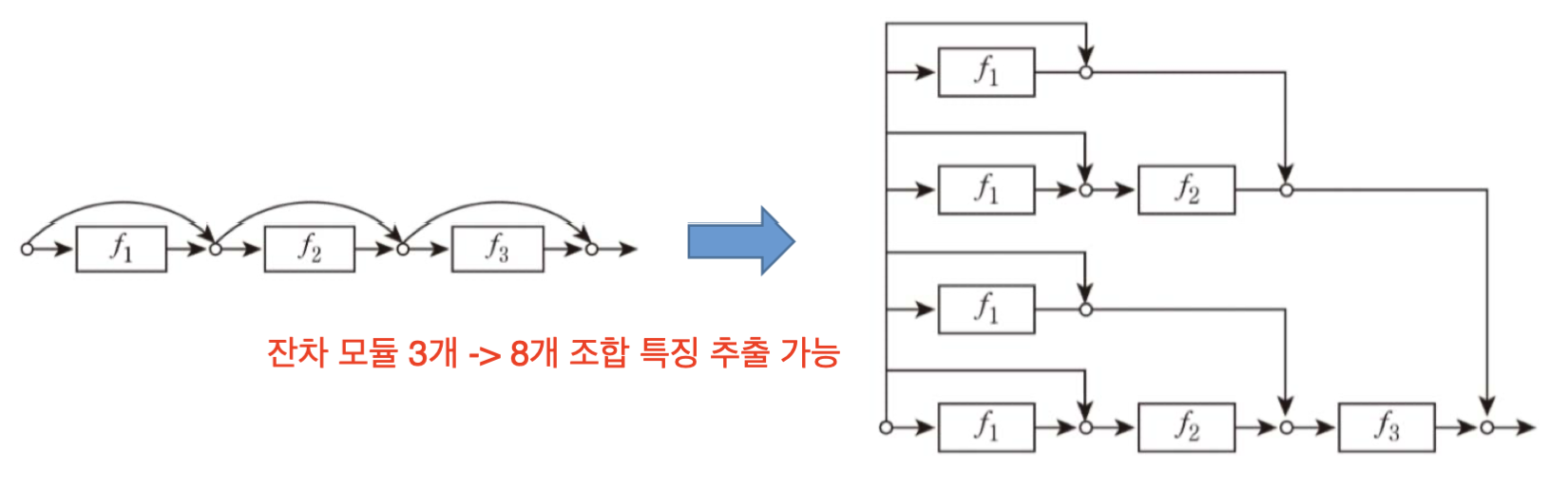
즉, 여러 층이 연결된 효과를 볼 수 있습니다.
때문에, 필요한 출력이 얻어지면 컨볼루전 층을 건너뛸 수도 있습니다.
DenseNet
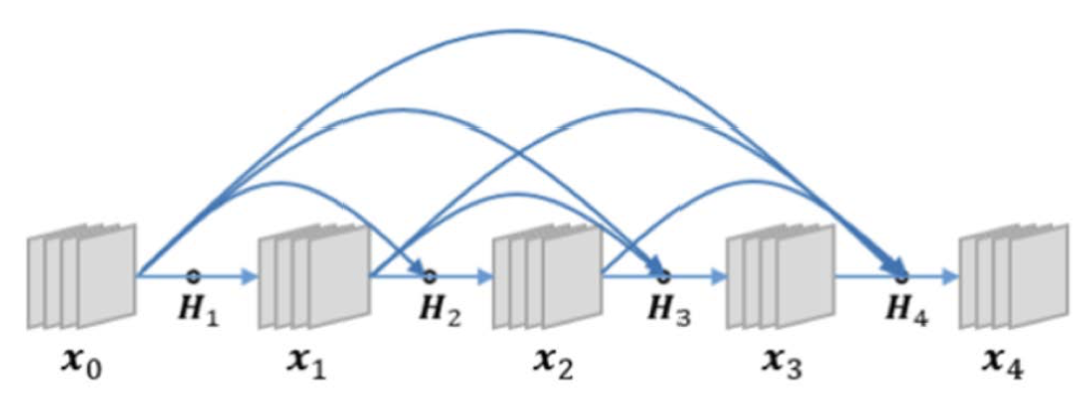
앞 층에서 올 수 있는 지름길 연결구성 방식이기에 연산 방식이 ResNet과 좀 다릅니다.
- ResNet: Conv-배치정규화-ReLU
- DenseNet: 배치정규화-ReLU-Conv
따라서 이전 단계의 동일한 특징 정보가 진차모듈을 통해 각 단계에 전달되기 때문에 새로운 특징을 만드는데 소극적이었던 ResNet과 달리
새로운 특징이 추출될 가능성이 높아졌습니다.

또한, 전이층을 두어 층이 과도하게 늘어나는 현상을 예방하고 학습 효율을 높였습니다.
DPN
ResNet + DenseNet 으로, DenseNet의 단점인 특징이 중복해서 추출될 수 있는 문제를 마이크로 블록을 사용하여 극복한 모델입니다.