웅덩이

인과성이 약하거나, 연관성이 애매하거나, '얼마나?'에 해당하는 정도가 모호한 문장을 정량화 하는 방법에 대해 알아봅니다.

확신도 (Certainty factor)

규칙과 사실의 신뢰정도를 [-1, 1] 구간의 값으로 표현합니다.

확신도	대응되는 단어
−1.0	절대 아니다 (definitely not)
−0.8	거의 확실히 아니다 (almost certainly not)
−0.6	아마 아니 것이다 (probably not)
−0.4	어쩌면 아닐 것이다 (maybe not)
−0.2 ~ 0.2	모르겠다 (unknown)
0.4	어쩌면 그럴 것이다 (maybe)
0.6	아마 그럴 것이다 (probably)
0.8	거의 확실하다 (almost certainly)
1.0	확실하다 (definitely)

추론에 대한 확신도는 각 명제에 대한 확신도를 계산하여 도출해야 합니다.

IF A THEN B ( $\{A \rightarrow B, \; A\} \vdash B$ )
기본적으로 정형식들의 확신도를 곱하는 방식으로 구합니다.

$cf(B) = cf(A) \times cf(A \rightarrow B)$
IF A and B THEN C ( $\{A \wedge B \rightarrow C, \; A, \; B\} \vdash C$ )
and의 경우 조건부에 해당하는 정형식의 확신도 중 작은 값을 고릅니다.

$cf(C) = min\{cf(A), cf(B)\} \times cf(A \wedge B \rightarrow C)$
IF A or B THEN C ( $\{A \vee B \rightarrow C, \; A, \; B\} \vdash C$ )
or의 경우 조건부에 해당하는 정형식의 확신도 중 큰 값을 고릅니다.

$cf(C) = max\{cf(A), cf(B)\} \times cf(A \vee B \rightarrow C)$

아래는 예시입니다.

231022-192422

만약, 여러 사실에 의해 동일한 사실을 추론하는 경우 추론 결과는 같지만, 확신도는 다르게 계산될 수 있습니다.
이런 경우, 확신도를 하나로 통합하는게 좋습니다.

231022-192640

어떤 사건이 일어날 가능성을 표현할 때 사용합니다.

사건 A, B가 동시에 일어날 확률을 가리키며, 아래와 같이 수식화 할 수 있습니다.

A: 첫 번째 주사위가 짝수
B: 두 번째 주사위가 홀수

$P(A,B) = P(A \cap B) = P(AB)$
$= 1/2 \times 1/2 = 0.25$

사건 B가 일어났을 때, 사건 A가 일어날 확률을 가리키며, 아래와 같이 수식화 할 수 있습니다.

A: 두 주사위의 합이 8
B: 첫 번째 주사위가 3

$P(A|B) = \frac{P(A,B)}{P(B)}$
$= \frac{1/36}{1/6} = 1/6$

베이즈 정리에 의해 조건부 확률의 조건부를 변형할 수 있습니다.

$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$

기존 집합론과 다르게 퍼지 이론은 0/1의 이분법적으로 분류하지 않고, 0~1로 모호하게(어느정도 포함되게) 구분함.
즉, 어느 정도(degree)의 문제는 퍼지 집합을 도입하여 해결.

원소가 모임(collection)에 어느 정도 속한다는 것을 표현한 것으로, 해당 집합은 부분적으로 참이 됨.
소속정도는 [0, 1] 범위의 실수값으로 표현함.

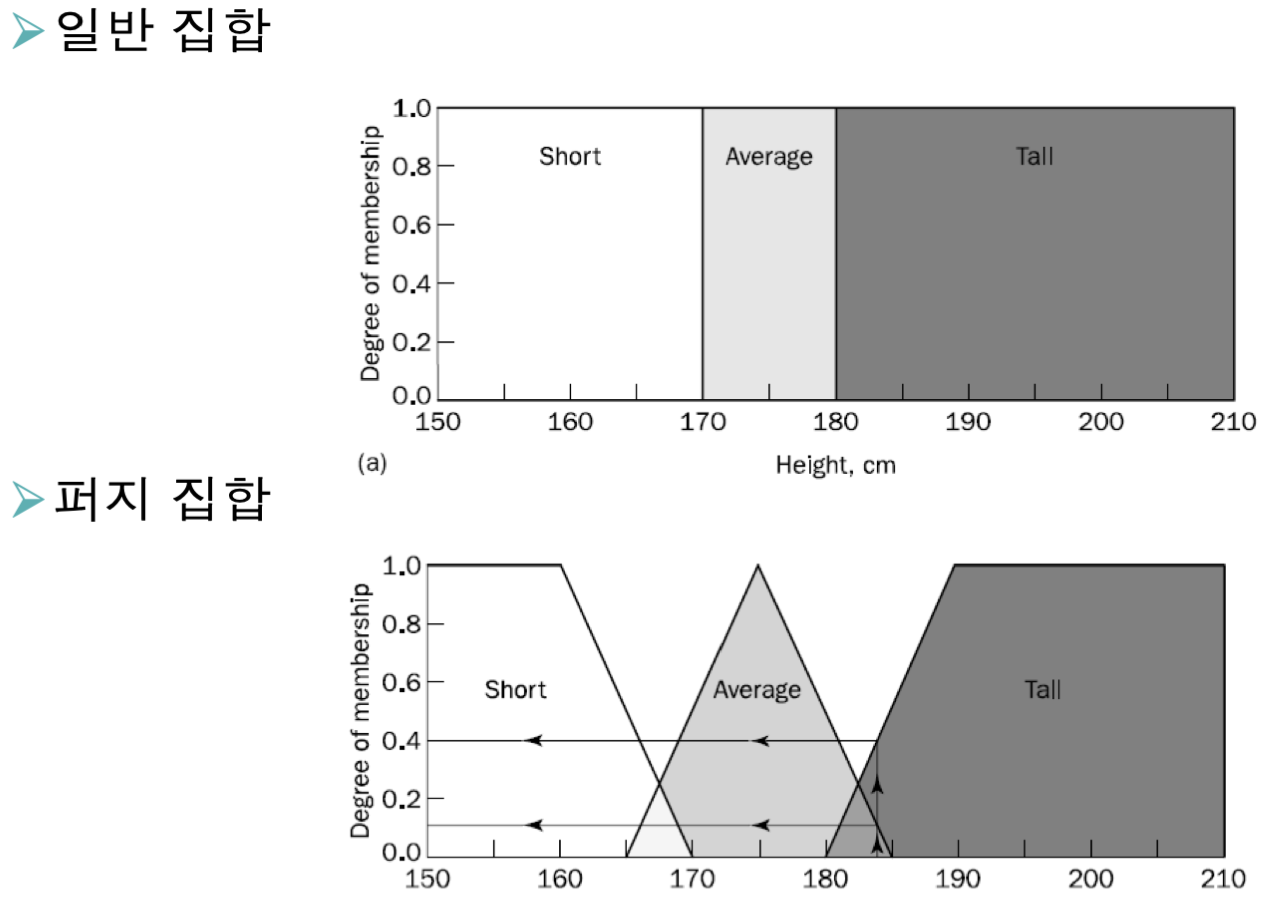
작다, 평균이다, 크다의 표현을 아래와 같이 다르게 할 수 있음.

231022-194330

소속함수로 표현된 언어항을 표함하는 규칙.

IF service = 나쁘다 OR food = 별로이다 THEN tip = 적다
IF service = 보통이다 THEN tip = 보통이다
IF service = 훌륭하다 OR food = 맛있다 THEN tip = 많다

언어항
'나쁘다', '맛있다', '많다'와 같은 자연어에 해당하는 항으로 소속함수로 표현될 수 있다.
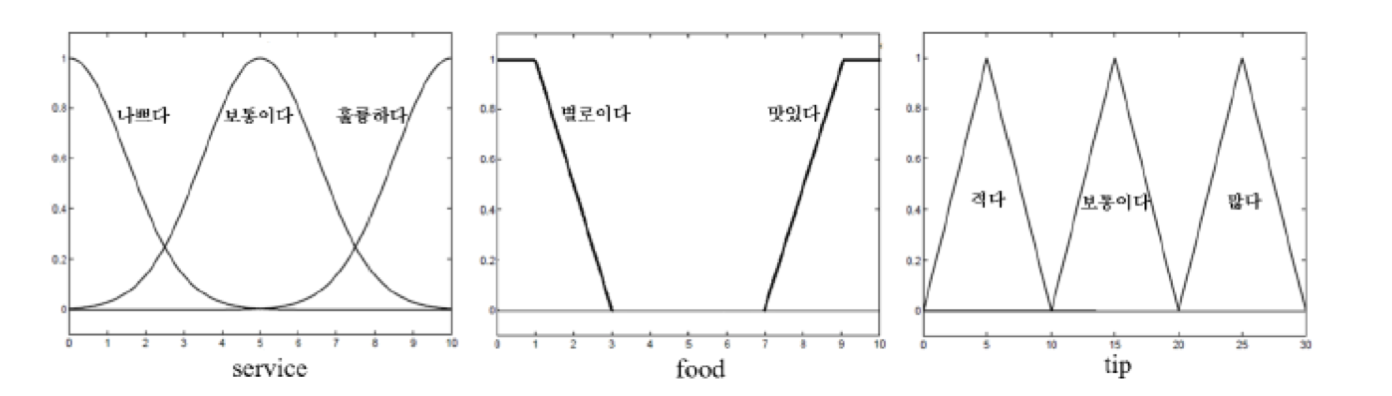
231022-194851

소속함수로 표현돤 언어항을 사용하는 퍼지 규칙들의 모음으로 수치적인 추론이 가능해진다.

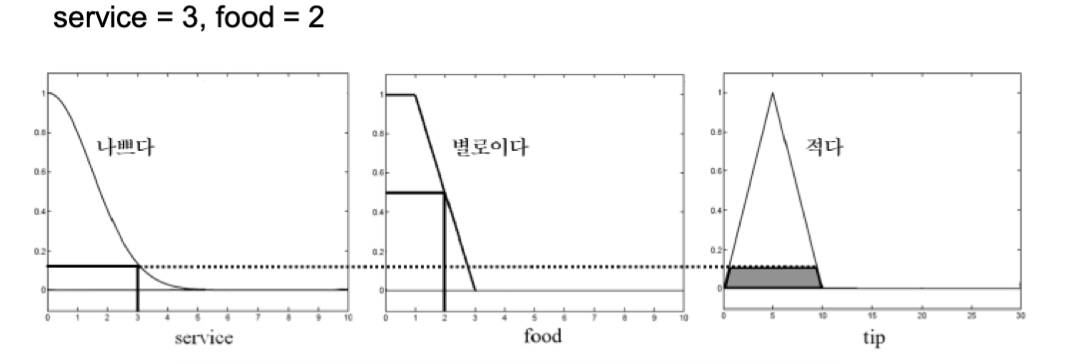
231022-195645

추론된 영역의 무게중심을 결과로 사용하면 비퍼지화가 가능하다.