명제 논리 & 술어 논리

말로 표현된 문장을 타당한 추론을 위해 기호를 사용하여 표현하고, 기호의 조작을 통해 참과 거짓을 판정하는 분야이다.

명제 논리

명제 (Proposition)

명제란, 참과 거짓을 분평하게 판정할 수 있는 문장으로 P, Q와 같은 기호로 표현된다.

중요한 점은, 명제 그 자체는 참, 거짓을 결정할 수 없고, 반드시 기호의 진리값을 설정해 줘야 한다는 점이다.
이게 무슨 말이냐면, 아래의 문장을 예로 들어 설명해보겠다.

오징어 다리는 10개 이다.

이 명제는 우리나라에서는 참이다.
하지만 북한에서는 오징어 라는 명사는 우리나라의 낙지를 가리키는 말 이기 때문에 북한에서는 거짓인 명제이다.

즉, 문장 자체의 내용에 대해서는 관심을 갖지 말고, 문장의 설정된 진리값에만 관심을 가져야 한다.

용어 설명

용어	의미
기본 명재	하나의 진술로만 이루어진 최소 단위의 명제
복합 명제	기본 명제들이 결합되어 만들어진 명제

논리식 (Logical expression)

명제를 기호로 표현한 형식으로 명제기호, T/F, 논리 기호를 사용하여 구성되는데, 가장 기본이 되는 논리 기호는 다음과 같다.

논리기호	이름	논리식	의미
$\neg$	부정 (negation)	$\neg P$	$P$가 아님
$\vee$	논리합 (disjunction)	$P \vee Q$	$P$ 또는 $Q$
$\wedge$	논리곱 (conjunction)	$P \wedge Q$	$P$ 그리고 $Q$
$\rightarrow$	함의 (implication)	$P \rightarrow Q$	$P$ 이면 $Q$
$\equiv$	동치 (equivalence)	$P \equiv Q$	$(P \rightarrow Q) \wedge (Q \rightarrow P)$

용어 설명

용어	의미
리터럴	명제 기호 또는 명제 기호의 부정
절	리터럴들이 논리합이나 논리곱으로만 연결 (논리합 절, 논리곱 절)
논리곱 정규형 (CNF)	논리합 절들이 논리곱으로 연결되어 있는 논리식
논리합 정규형 (DNF)	논리곱 절들이 논리합으로 연결되어 있는 논리식
정형식 (WFF)	진리값(T/F)과 명제, 그들과 논리 기호를 사용하여 구성된 논리식을 의미함

진리표 (Truth table)

논리기호에 따라 T/F를 결합하는 방법을 나타낸 표

$P$	$Q$	$\neg P$	$P \vee Q$	$P \wedge Q$	$P \rightarrow Q$	$P \equiv Q$
F	F	T	F	F	T	T
F	T	T	T	F	T	F
T	F	F	T	F	F	F
T	T	F	T	T	T	T

• 타당한 논리식 (Valid logical expression), 항진식
  모든 가능한 해석에 대해 항상 참인 논리식
  e.g. $P \vee \neg P$

• 항위식
  모든 가능한 해석에 대해 항상 거짓인 논리식
  e.g. $P \wedge \neg P$

• 츙족가능한 논리식
  참으로 만들 수 있는 해석이 하나라도 있는 논리식

• 충족불가능한 논리식
  참으로 만들 수 있는 해석이 하나도 없는 논리식. 즉, 항위식.

동치 관계 (Equivalence relation)

어떠한 해석에 대해서도 같은 진리 값을 갖는 두 논리식

• $\neg(\neg p) \equiv p$
• $p \vee F \equiv p$
  $p \wedge T \equiv p$
• $P \vee \neg P \equiv T$
  $P \wedge \neg P \equiv F$
• $\neg (p \wedge q) \equiv \neg p \vee \neg q$
  $\neg (p \vee q) \equiv \neg p \wedge \neg q$
• $p \rightarrow q \equiv \neg p \vee q$
• $p \vee (q \vee r) \equiv p \vee q \vee r$
  $(p \wedge q) \wedge r \equiv p \wedge q \wedge r$
• $p \vee (q \wedge r) \equiv (p \vee q) \wedge (p \vee r)$
  $p \wedge (q \vee r) \equiv (p \wedge q) \vee (p \wedge r)$

논리적 귀결 (Logical entailment)

정형식(Well-Formed Formula, WFF)의 집합 $\Delta$가 다른 정형식 $\omega$를 참으로 만든다면 두 관계를 아래와 같이 정의한다.

$\Delta \models \omega$
e.g. $\{P, \; P \rightarrow Q\} \models Q$

$\Delta$는 $\omega$를 논리적으로 귀결한다.
$\omega$는 $\Delta$를 논리적으로 따른다.
$\omega$는 $\Delta$의 논리적 결론이다.

추론 (Inference)

논리적 귀결을 도출하는 과정을 추론이라고 한다.

관측된 복수의 사실들을 일반화하여 일반적인 패턴(명제)를 도출하는 것을 귀납적 추론 이라고 하고,
참인 명제(사실)들로부터 새로운 명제(사실)을 도출하는 것을 연역적 추론 이라고 한다.

논리에서의 추론은 보통 연역적 추론을 가리키는데, 이걸 도출하는 테크닉에 대해 살펴보자.

• 긍정 논법
  $\{p \rightarrow q, \; p\} \vdash q$
  ({새이다 → 날 수 있다, 새이다} → 날 수 있다)

• 부정 논법
  $\{p \rightarrow q, \; \neg q\} \vdash \neg p$
  ({새이다 → 날 수 있다, 날 수 없다} → 새가 아니다)

• 삼단 논법
  $\{p \rightarrow q, \; q \rightarrow r\} \vdash p \rightarrow r$
  ({새이다 → 날개가 있다, 날개가 있다 → 날 수 있다} → 새이다 → 날 수 있다)

• 논리 융합 (Resolution)
  긍정, 부정, 삼단 논법을 포함한 일반화된 추론 규칙으로
  두 개의 논리합 절이 같은 기호의 긍정-부정 리터럴을 서로 포함하고 있을 때, 해당 리터럴을 제외한 나머지 리터럴의 논리합 절을 만들어 내는 것.

  논법	변환	WFF (논리 융합식, Resolvent)
  $p \rightarrow q, \; p$	$\neg p$ $\vee q$, $p$	$q$
  $p \rightarrow q, \; \neg q$	$\neg p \vee$ $q$, $\neg q$	$\neg p$
  $p \rightarrow q, \; q \rightarrow r$	$\neg p \vee$ $q$, $\neg q$ $\vee r$	$\neg p \vee r$ ($p \rightarrow r$)

  즉, 논리 융합을 사용하면 모든 추론 규칙을 일반화 할 수 있다.

• 정당성 (sound)
  $\Delta \vdash \omega \; \rightarrow \; \Delta \models \omega$ (아야 sound)

• 완전성 (complete)
  $\Delta \models \omega \; \rightarrow \; \Delta \vdash \omega$ (야아 complete 하네)

  정당성과 완전성을 동시에 만족하는 추론 규칙은 논리적인 귀결과 동일시 할 수 있다.

증명 (Proof)

• 구성적 증명 (Constructive proof)
  공리(참인 논리식)들에 추론 규칙을 적용하여 참을 만들어 보이는 증명.
  정리하다가 결론이 참으로 끝나면 된다.

• 논리융합 반박 (Resoultion refutation)
  증명할 정리를 일단 부정하고, 논리융합 방법을 적용해 모순이 발생함으로 보이는 증명.
  부정된 정리가 모순이니, 원상태의 정리는 참이 된다.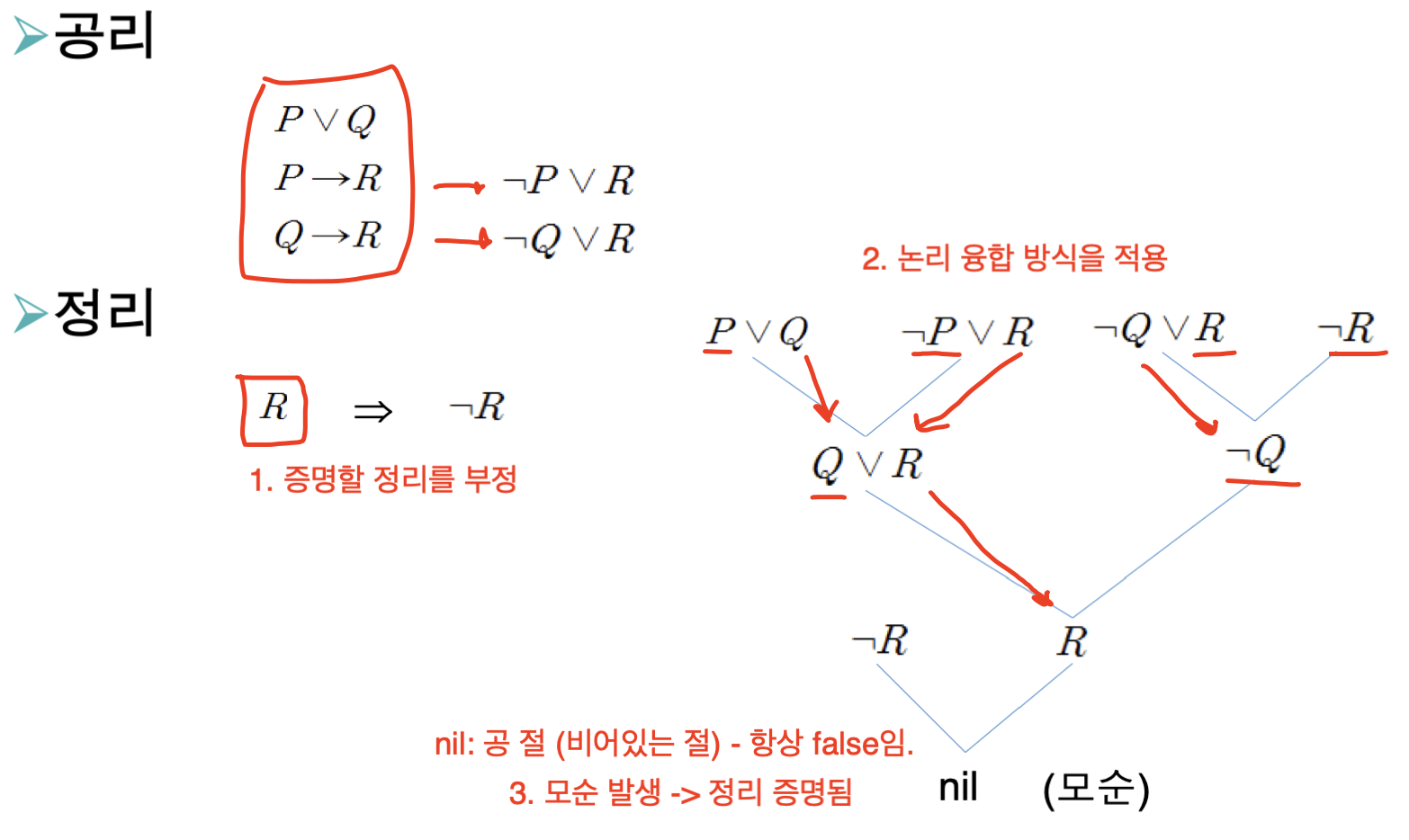

  

---

술어 논리

명제의 내용을 다루기 위해 변수, 함수 등을 도입하고, 이들의 값에따라 T/F가 결정되도록 명제 논리를 확장한 논리.

술어 (Predicate)

대상의 속성이나 관계를 기술하는 기호로, 대상에게 T/F를 부여하는 명제의 기본 형식이다.

문장	명제 논리	술어 논리
모든 사람은 죽는다	P	$\forall x(사람(x) \rightarrow 죽는다(x))$
소크라테스는 사람이다	Q	$사람(소크라테스)$
소크라테스는 죽는다	R	$죽는다(소크라테스)$

존재 한정사
Existential quantifier로 존재함을 알려준다. ($\exist$)

전칭 한정사
Universal quantifier로 모든 범위를 가리킨다. ($\forall$)

함수 (function) / 항 (term)

주어진 인자에 대해 T/F를 반환하는 것이 아닌, 일반작인 값을 반환하는 것을 함수라고 한다.
즉, 인자를 지칭하기 위해 쓰인다.

함수의 인자가 될 수 있는 것을 항 이라고 한다.
상수, 변수, 함수만이 항이 될 수 있다.

명제 논리식의 정형식(WFF)과 마찬가지로, 술어 논리식의 정형식 역시 비슷한 정의를 갖는다.
항, 논리 기호, 한정사로만 이루어진 식을 정형식이라고 부른다.

N차 술어 논리 (N-order predicate logic)

변수에만 한정사를 사용할 수 있도록 한 술어 논리를 일차 술어논리(FOL) 라고 한다.
엄밀히는, 술어기호의 인자로 사용될 수 있는 객체나 대상만을 변수화 할 수 있고, 이들 변수에만 전칭 한정사와 존재 한정사를 쓸 수 있도록 한 술어논리를 말한다.

변수, 함수, 술어기호에 대해 한정사를 쓸 수 있도록 한 술어 논리를 고차 술어논리(HOL) 라고 한다.
엄밀히는, 함수나 술어기호도 변수화 할 수 있고, 이들 변수에만 전칭 한정사와 존재 한정사를 쓸 수 있도록 한 술어논리를 말한다.

인공지능 분야에서는 연산량의 한계 때문에 일차 술어논리를 주로 사용한다.

CNF 변환

아래의 변환 과정을 거친면 된다.

1. 한정사를 논리식의 맨 앞으로 끌어내는 변환
   일반적으로 한정사를 맨 앞으로 끌어내도 의미는 변하지 않지만, 그래도 최다한 할 수 있는 변환을 한 뒤에 끌어내자.

2. 전칭 한정사 제거
   $\forall$은 바로 제거해도 상관없다.

3. 존재 한정사 제거
   우선 아래와 같은 방식으로 전칭 한정사로 변환한 뒤 전칭 한정사를 제거하는 방법을 사용한다.
   $\neg \exist x P \equiv \forall x \neg P$

   만일 함수에 변수가 2개 이상 사용된 경우 변환이 어려울 때는 상수를 집어넣거나 스콜렘 함수로 변환한다.
   $\forall x \exist y [P(x) \wedge$ $Q(x, y)$$] \rightarrow \forall x [P(x) \wedge$ $Q(x, s(x))$$]$

4. 단일화
   논리 융합을 적용할 때, 대응되는 리터럴이 같아지도록 상수를 변수화 함.
   

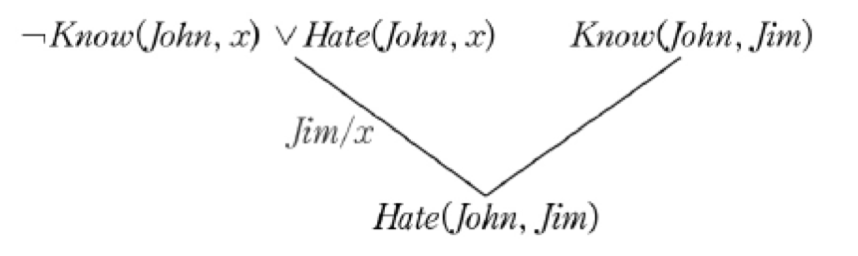
변환 과정을 거쳐 논리융합 반박을 통해 증명하는 예시를 살펴보자.
아래의 예시는 (5)의 모순을 보임으로써 $\neg$(5)가 참임을 보이는 논리융합 반박이다.