상태공간 & 탐색

상태공간

문제 해결 과정에서 초기 상태로부터 도달할 수 있는 모든 상태들의 집합을 의미한다.
한 마디로 문제의 해가 될 가능성이 있는 모든 상태들의 집합을 의미한다.

탐색

상태공간에서 최적의 해를 찾기위해 공간을 체계적으로 찾아보는 것을 의미한다.
탐색은 아래와 같은 방식으로 크게 구분지을 수 있다.

1. 맹목적 탐색
2. 정보이용 탐색

이렇게 구분짓는 이유는 탐색의 방식에 따라 달라지는데,
탐색 방식이 다양해 질 수 밖에 없는 이유는 일반적인 문제에서는 상태공간이 매우 크기 때문에
미리 공간 그래프를 그릴 수 없어 탐색 과정에서 그래프를 생성할 수 밖에 없기 때문이다.

---

맹목적 탐색

정해진 순서에 따라 상태공간 그래프를 점차 생성해 가면서 해를 탐색하는 방법을 의미한다.

깊이 우선 탐색 (Depth-first search)

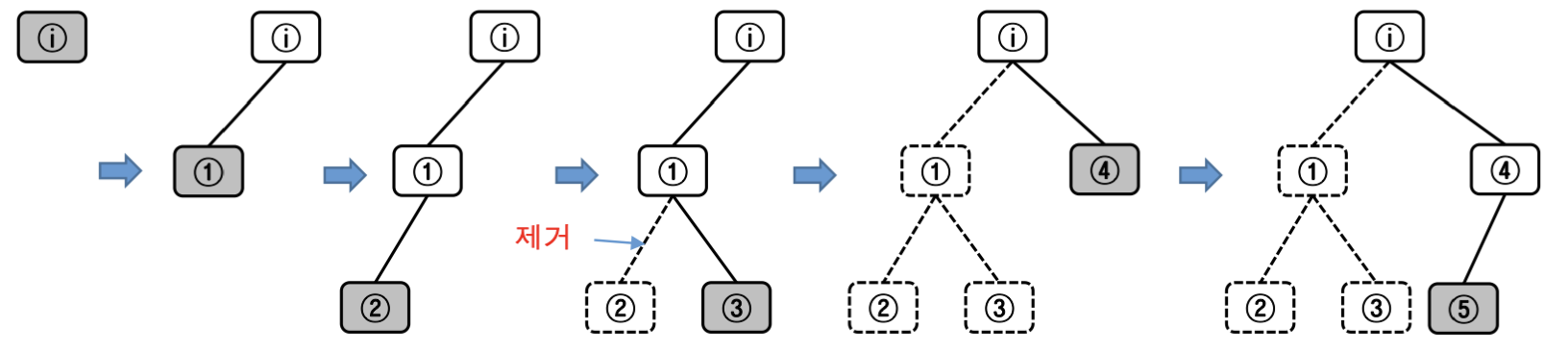
초기 노드부터 깊이가 깊어지는 방향으로 우선 탐색하는 기법.
더이상 진행할 수 없다면 백 트리킹으로 돌아와 다음 노드 탐색.

루트 노드에서 현재 노드까지의 경로 하나만 유지한다는 특징이 있기에 메모리 공간 사용이 효율적이라는 장점이 있다.
하지만, 깊이가 무한히 깊어지는 무한루프의 가능성 때문에 항상 최단 경로의 해를 보장할 수 없다는 단점이 있다.

너비 우선 탐색 (Breadth-first search)

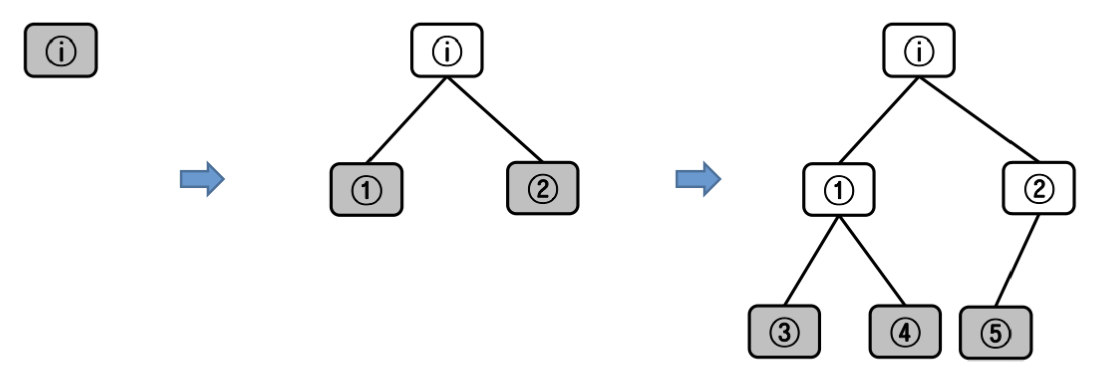
초기 노드부터 시작하여 모든 자식 노드를 확장하여 탐색하는 기법.
목표 노드가 없다면 단말 노드에서 다시 자식노드 확장 탐색.

최단 경로의 해를 보장하지만, 메모리 효율적이지 못하다.

깊이 제한 탐색 (Depth-limited search)

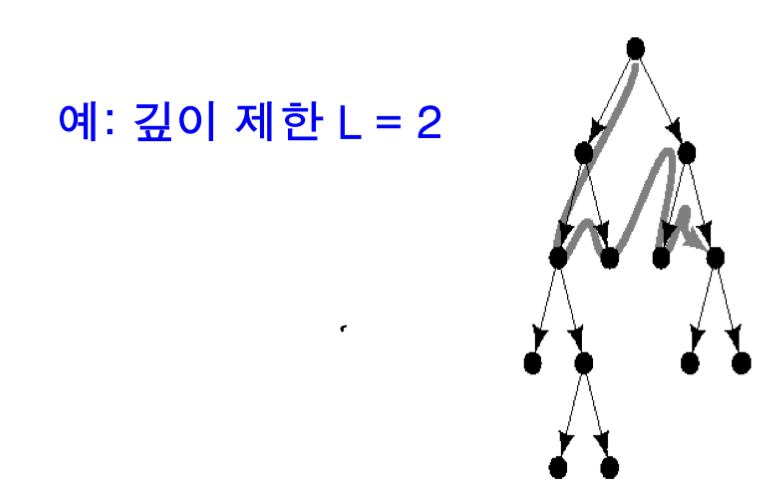
기본적인 탐색 방식은 깊이 우선 탐색 방식임.
단, 깊이에 제한을 둬서 특정 깊이 이하로는 탐색을 진행하지 않고 백 트래킹 하는 것이 특징임.
특정 깊이에서 목표를 찾지 못한 경우 깊이를 늘려가며 처음부터 다시 탐색을 진행함.

최단 경로의 해를 보장하며, 메모리 사용도 효율적이다.
상위 노드는 반복해서 탐색하기에 약간의 비효율성이 있으나, 무시할만한 수준임.

즉 맹목적 탐색시에는 이 방식을 우선적으로 고려하는 것이 좋음.

---

정보이용 탐색

휴리스틱한 방법으로 목표까지의 예상 비용을 구하고, 그 값에 의거해 순간순간 최선의 선택을 해가며 탐색하는 방법을 의미한다.

휴리스틱 (heuristic)
신속하게 어림짐작 하는 것.

언덕 오르기 방법 (Hill climbing method)

현재 노드에서 휴리스틱에 의한 평가값이 가장 좋은 이웃 노드 하나를 확장해가는 탐색기법.
단, 국소 최적해에 빠질 가능성이 있다.
(경사 하강법과 유사)

최상 우선 탐색 (Best-first search)

확장 중인 노드들 중에서 목표 노드까지 남은 거리가 가장 짧은 노드를 확장하여 탐색하는 기법.
일종의 그리디한 방식임.

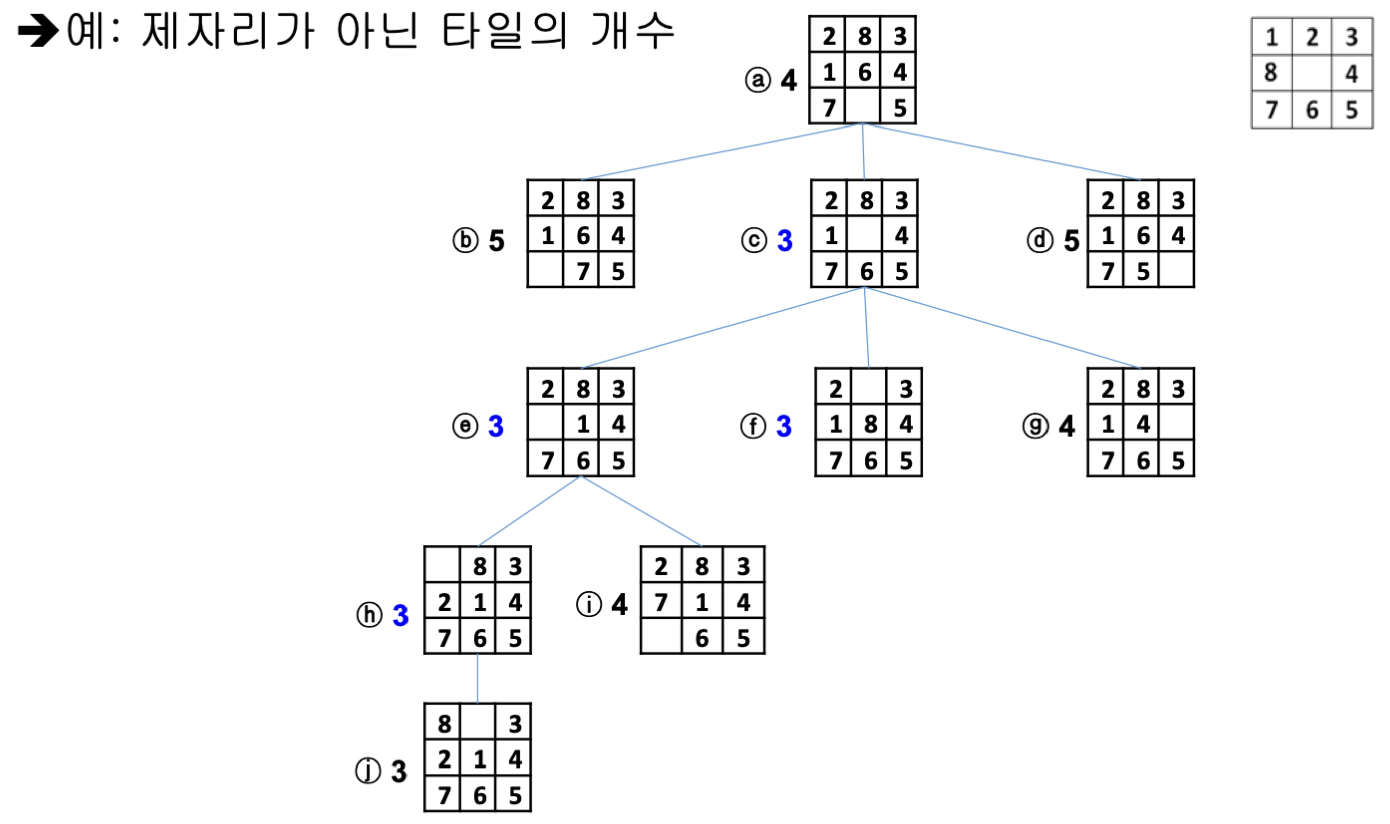
예시로 휴리스틱 함수를 제자리가 아닌 타일의 개수라고 할 때, 다음과 같은 순서로 탐색을 진행하게 된다.

a → c → e/f → h → j

빔 탐색 (Beam search)

최상 우선 탐색(BFS) 의 확장판으로, 휴리스틱에 의한 평가값이 우수한 일정 개수(K개)의 확장 가능한 노드만을 메모리에서 관리하면서 탐색.

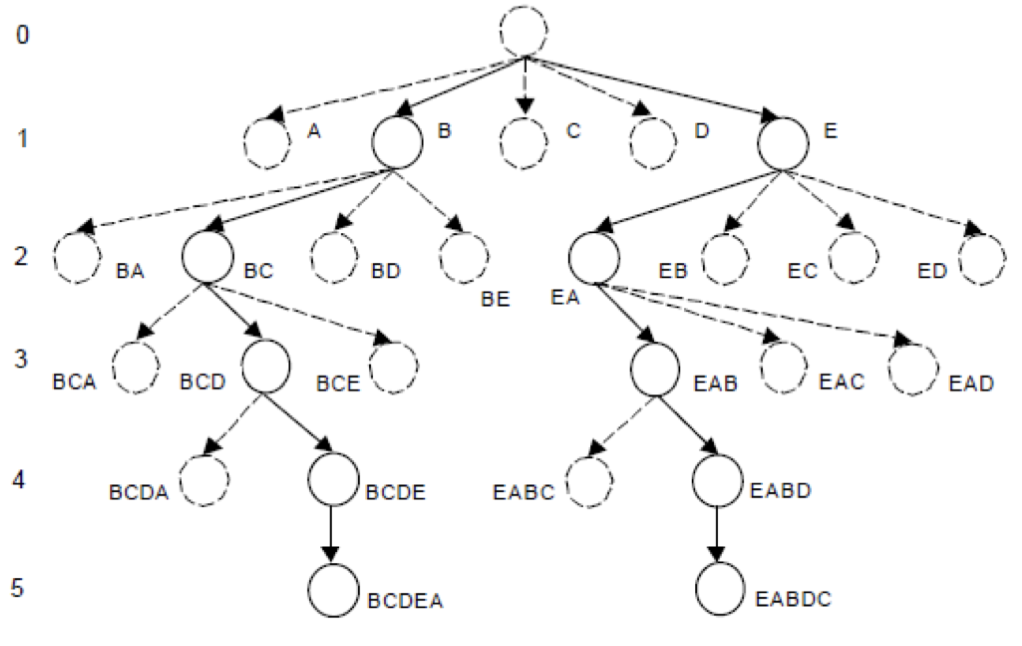
예시로 K=2일 때, A~E를 일단 탐색하고, 평가값이 우수한 B, E를 제외한 노드는 메모리에서 제거하며 B, E에서 그 자식노드에 대해 같은 방식을 적용하며 탐색한다.

A* 알고리즘 (A-star algorithm)

최상 우선 탐색(BFS) 의 개선판으로, 휴리스틱에 의한 평가값 + 현재까지의 코스트의 결과인 휴리스틱한 전체 비용을 기준으로 탐색하는 기법.

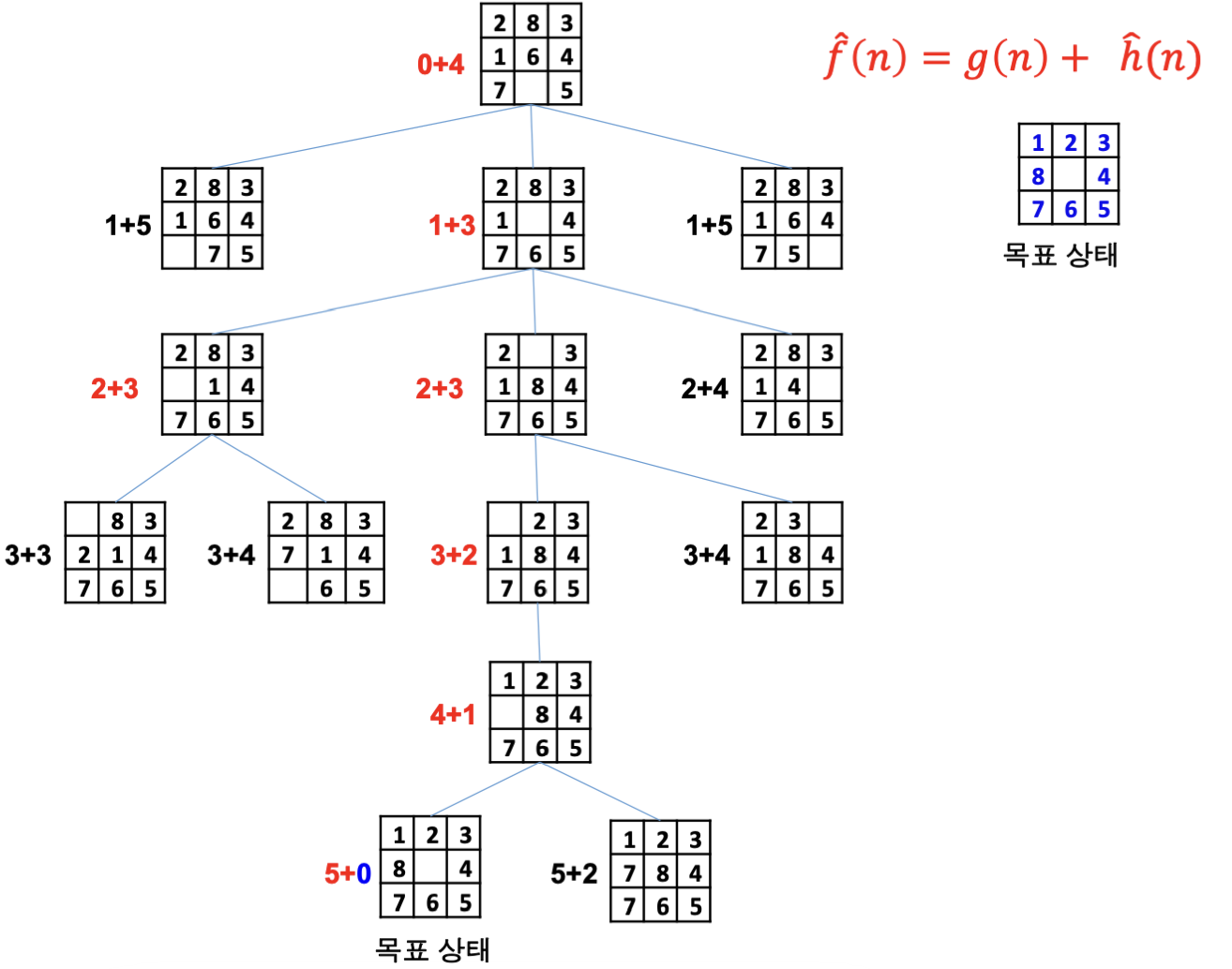
최초 상태를 탐색한 후, 그 자식 노드 3개의 휴리스틱한 전체 비용을 계산하면 1(현재까지의 코스트)+3(휴리스틱 평가값)의 값을 갖는 가운데 자식 노드가 비용이 가장 작기에 다음 탐색 대상으로 한다.

이런 식으로 탐색한 모든 노드를 메모리 상에서 관리하며, 그 순간 휴리스틱 전체 비용이 가장 낮은 노드를 다음 탐색 대상으로 삼는다.