게임에서의 탐색 및 최적화
게임 트리를 탐색하는 기법과 최적화에 대해 알아봅니다.읽는데 11분 정도 걸려요.게임 트리
상대가 있는 게임에서 자신과 상대방의 가능한 게임 상태를 나타낸 트리.
자신의 턴인지, 상대의 턴인지에 따라 탐색하는 방식이 다르게 적용됨.
(나에겐 유리하게, 상대에겐 불리하게)
정해진 시간 내에 최대한 많은 수를 보는 것이 유리하기 때문에 탐색 효율을 높이는 것이 중요하다.
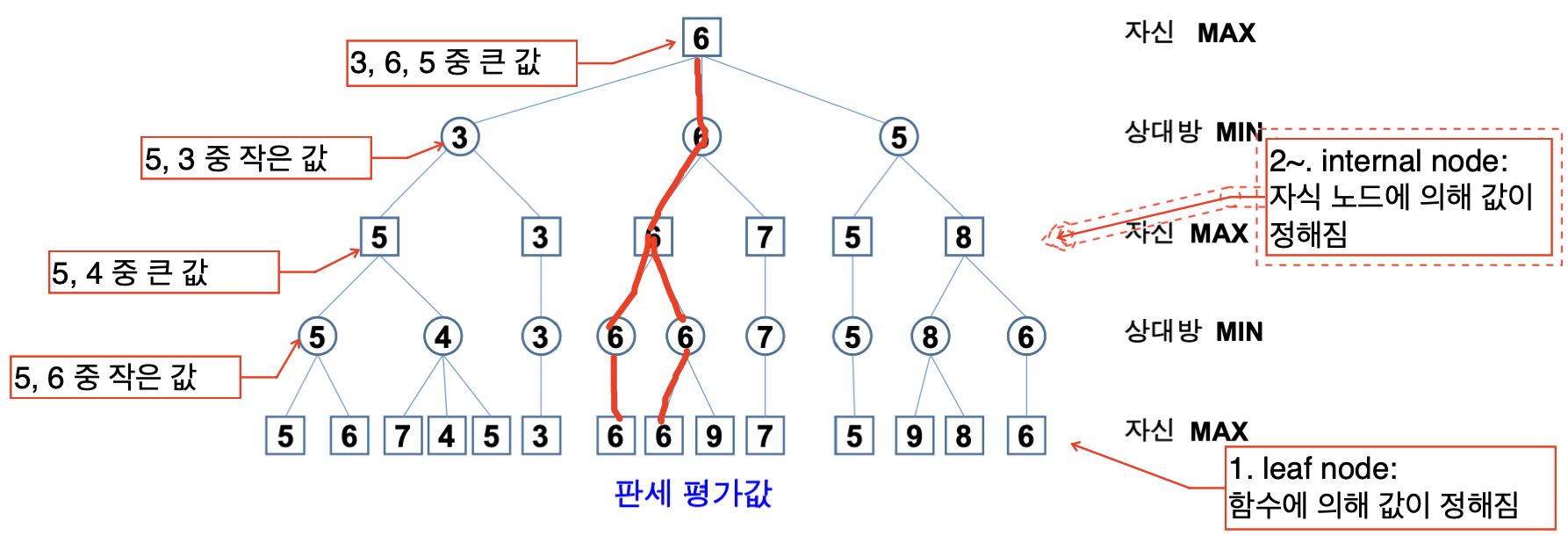
Mini-max Algorithm
특이하게 단말 노드로부터 위로 올라가면서 최소-최대 연산을 반복하여 자신이 선택할 수 있는 방법 중 가장 좋은 값을 선택하는 방법이다.
자신의 턴인 Max 노드에서는 자신에게 유리한 값을 선택하고,
상대의 턴인 Min 노드에서는 상대에게 불리한 값을 선택하는 방식을 취한다.
하지만 트리가 넓을 수록 모든 상태공간을 탐색하는건 시간상 너무 오래 걸리기 때문에 최적화 기법이 들어가야 한다.
바로 가지치기(prunning) 기법이다.
검토해 볼 필요가 없는 부분을 탐색하지 않도록 하는 기법인데, 어떻게 해야 검토할 필요가 없다는 걸 알 수 있을까?
깊이 우선 탐색(DFS)로 제한 깊이까지 탐색을 하면서 Min, Max 노드의 , 값을 업데이트 하는데, 각 , 값은 다음과 같은 값을 저장한다.
-
Max 노드에서만 값이 업데이트되며, 현재까지 확보한 자식의 값 중 최댓값을 저장함 -
Min 노드에서만 값이 업데이트되며, 현재까지 확보한 자식의 값 중 최솟값을 저장함
이 때, 탐색 후 값을 업데이트 하다가 되는 순간이 오는데, 그 때부터 나머지 자식노드는 탐색할 필요가 없어진다.
그 이유는, 상한선()과 하한선()이 정해질 때, 그 부모노드의 상한선과 하한선을 넘지 못하면 부모노드를 업데이트 할 수 없기에, 업데이트를 할 가능성이 없다면 가지치기를 해버리는 것이다.
알고리즘의 이해가 안된다면 아래 영상을 참고하면 좋을 거 같다.
속성으로 빠르게 탐색하고 싶다면 이런 방식으로 탐색해도 된다.
빠르게 업데이트 가능한 조건을 적어놓고, 그 조건이 업데이트가 절대로 불가능하다면 나머지 노드를 가지치기 하는 방식이다.
몬테카를로 트리 탐색 기법 (Monte Carlo Simulation)
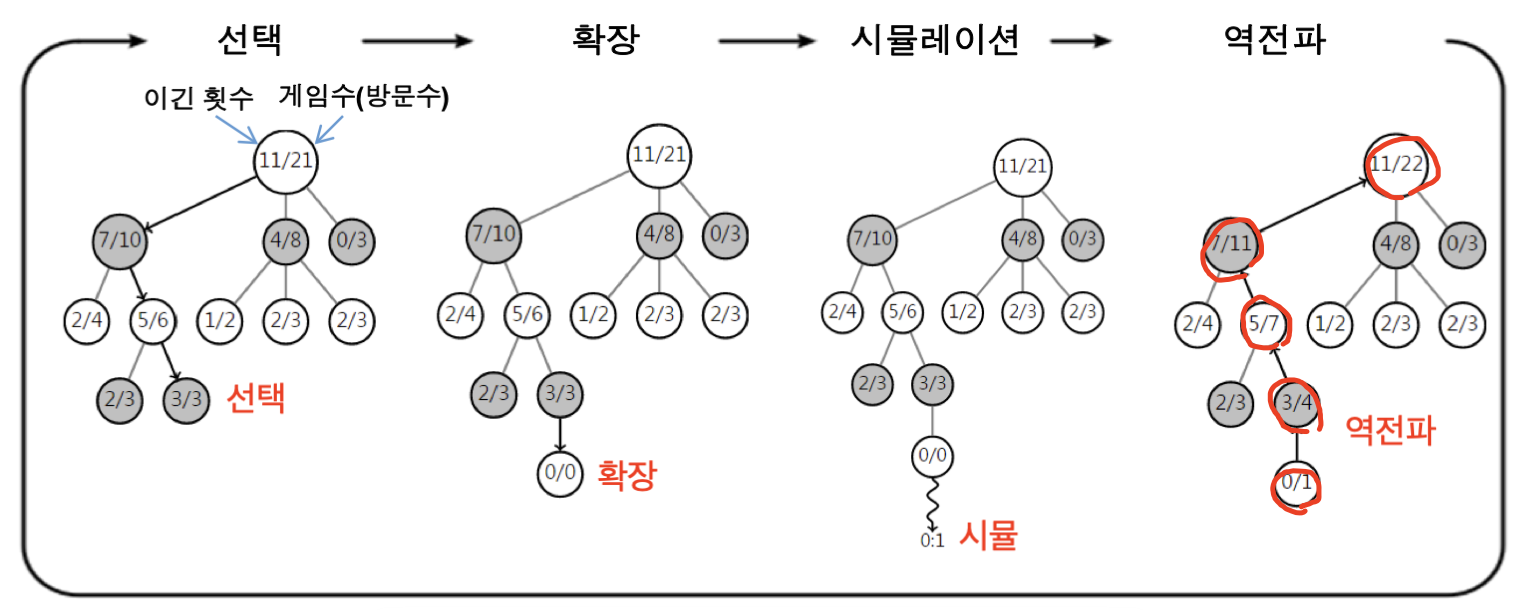
탐색 공간을 무작위 표본추출을 하면서 탐색 트리를 확장하여 가장 좋아보이는 것을 선택하는 휴리스틱 탐색 방법으로,
시간이 허용되는 동안 위의 4단계를 반복하여 시뮬레이션 및 트리를 확장한다.
-
선택
선택은 트리 정책을 적용하여 선택한다.
정책은 개발자 마음대로 정하는 거지만, 보통 승률과 노드 방문횟수를 고려하여 선택한다.
일반적으로승률이 높으며,방문횟수가 적은노드에 우선권을 부여한다 (UCB, Upper Confidence Bound 정책). -
확장
단말 노드에서 트리 정책에 따라 노드를 추가한다. -
시뮬레이션
기본 정책에 의한몬테카를로 시뮬레이션을 적용한다.
무작위 선택, 또는 약간 똑똑한 방법으로 게임이 끝날 때 까지 진행한다.
몬테카를로 시뮬레이션
특정 확률 분포로 부터 무작위 표본(또는 약간 똑똑한 방법으로)을 생성하고, 이 표본에 따라 행동을 하는 과정을 반복하여 결과를 확인하고 이 과정을 반복해 최정 결정을 하는 것.
특정 상태의 유불리를 상태판단함수로 판단하는 것이 아닌, 시뮬레이션으로 판단하게 된다.
- 역전파
게임의 결과를 단말 노드에서 루트 노드까지 올라가면서 반영한다.
제약조건 만족 문제
주어진 제약조건을 만족하는 조합 해(combination solution)을 찾는 문제로 N-Queens problem과 같은 문제가 이에 해당한다.
백 트래킹 탐색 (Backtracking search)
깊이 우선 탐색(DFS)을 하는 것처럼 변수에 허용되는 값을 하나씩 대입해보고, 가능한 모든 값을 대입했는데도 만족하는 것이 없으면 이전 단계로 돌아가서 이전 단계의 변수에 다른 값을 대입하는 전형적인 백 트래킹 방식이다.
제약조건 전파 (Constraint propagation)
인접 변수 간의 제약 조건에 따라 각 변수에 허용될 수 없는 값들을 제거하는 방식으로, 이름 그대로 주변에 제약조건을 전파하여 선택 가능한 가지수를 줄여가는 방식이다.
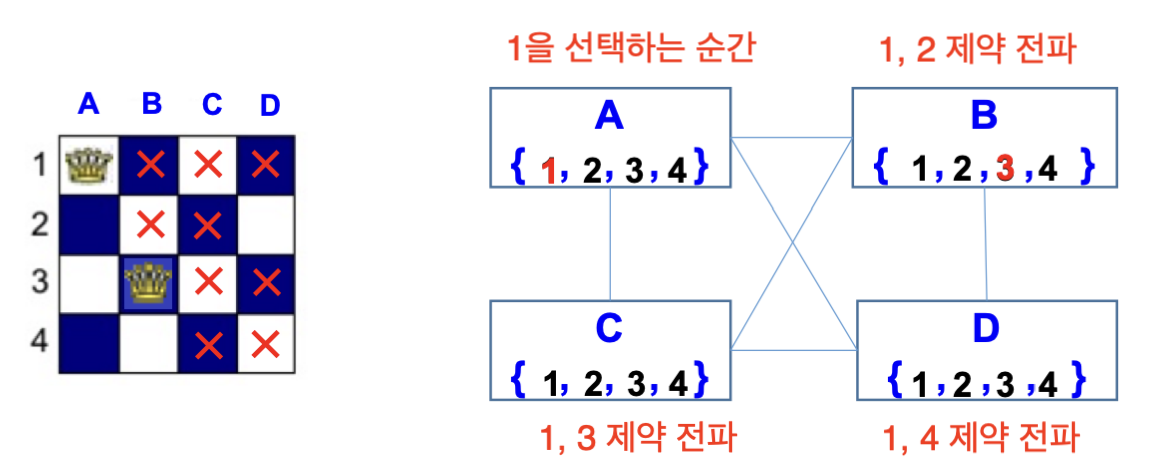
A에 1을 선택하는 순간 B~D에 각각 제약사항이 전파되어 B~D에서 선택할 수 있는 가지수가 제한된다.
여기서 B가 3을 선택하는 순간 C, D에 각각 제약사항이 또 전파되는데, 이 때 C는 더이상 아무것도 선택할 수 없기에 이전 스탭에서 다른 제약사항을 걸어야 한다.
최적화
여러가지 가능, 혀용되는 값들 중에서 주어진 기준을 가장 잘 만족하는 것을 선택하는 것으로, 크게 조합 최적화와 함수 최적화로 나뉜다.
조합 최적화
TSP와 같이 주어진 항목들의 조합으로 해가 표현되는 최적화 문제로, 이 경우에는 경로의 길이를 최소화 하는 문제이다.
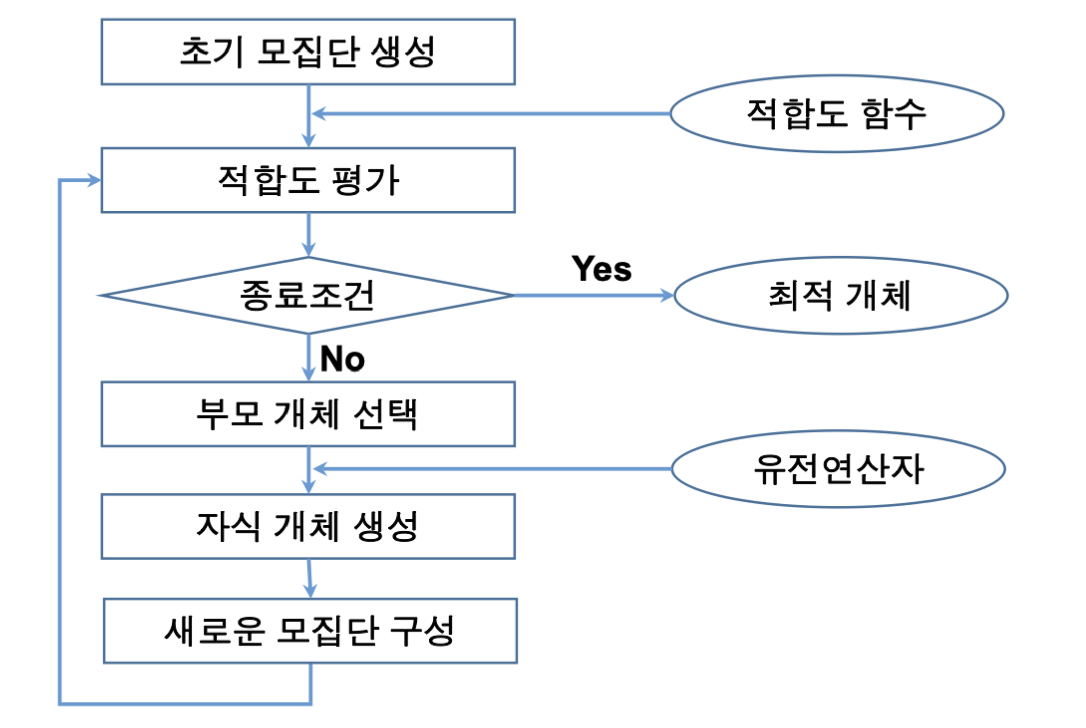
이를 달성하기 위해 생물의 진화를 모방한 집단 기반 확률적 탐색 기법인 유전 알고리즘을 사용하기도 한다.
개체는 염색체로 표현되며 다음과 같이 기술된다.
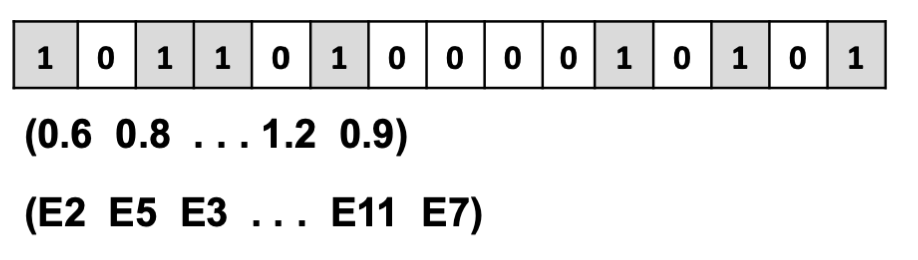
이런 염색체들의 집합을 모집단이라고 하는데, 이런 모집단(후보해)가 문제의 해로서 적합한 정도를 적합도 함수가 판단하게 되고, 적합하다면 최적 개체로서 알고리즘이 종료되지만, 적합하지 않다면 진화의 과정을 거치게 된다.
모집단이 진화를 할 때는 우선 부모 모집단 중 개체를 선택하게 되는데, 가능한 높은 적합도의 개체가 선택되도록 확률을 높게 조정한다.
자연선택과 같이 랜덤한 요소가 있어야 하기에 반드시 적합한 녀석이 선택되지는 않는다.
이후에는 선택된 부모 개체가 유전 연산을 거쳐 자식 개체를 양산하게 되는데, 유전 연산에는 다음과 같은 연산을 고려할 수 있다.
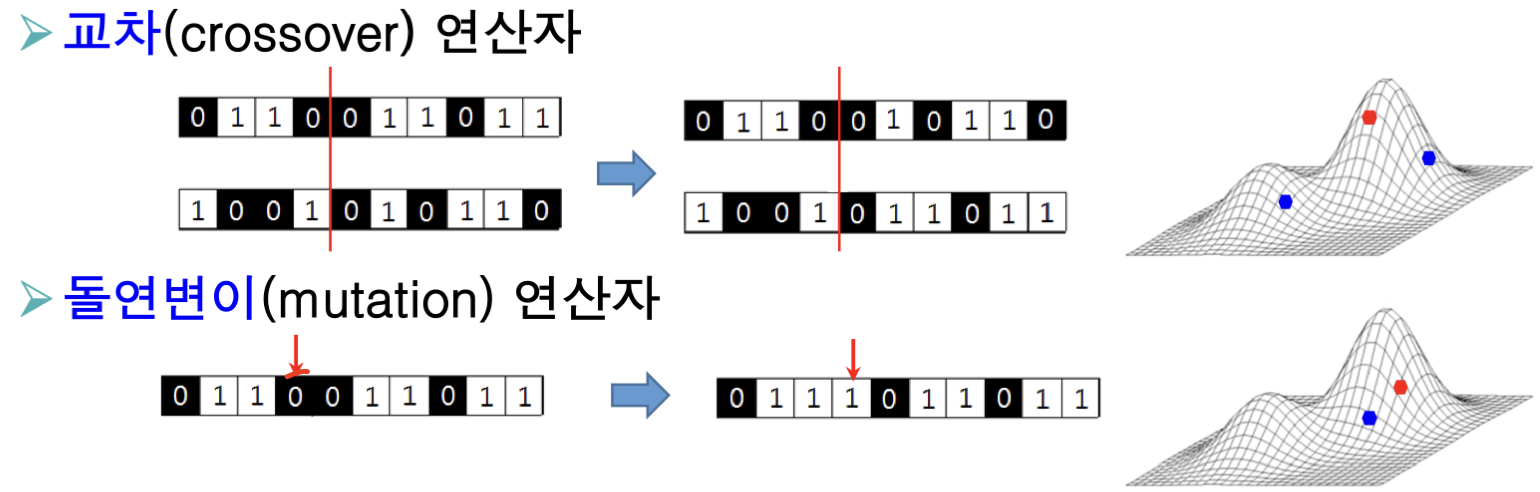
이후에는 생성된 여러 자식 개체를 이용해서 세대를 교체하게 되는데, 최대한 많은 우수한 계체가 다음 세대에 유지될 수 있도록 엘리트주의를 적용한다.
목적 최적화
어떤 목적 함수(Objective function)가 있을 때, 이 함수를 최대로 하거나 최소로 하는 변수 값을 찾는 최적화 문제이다.
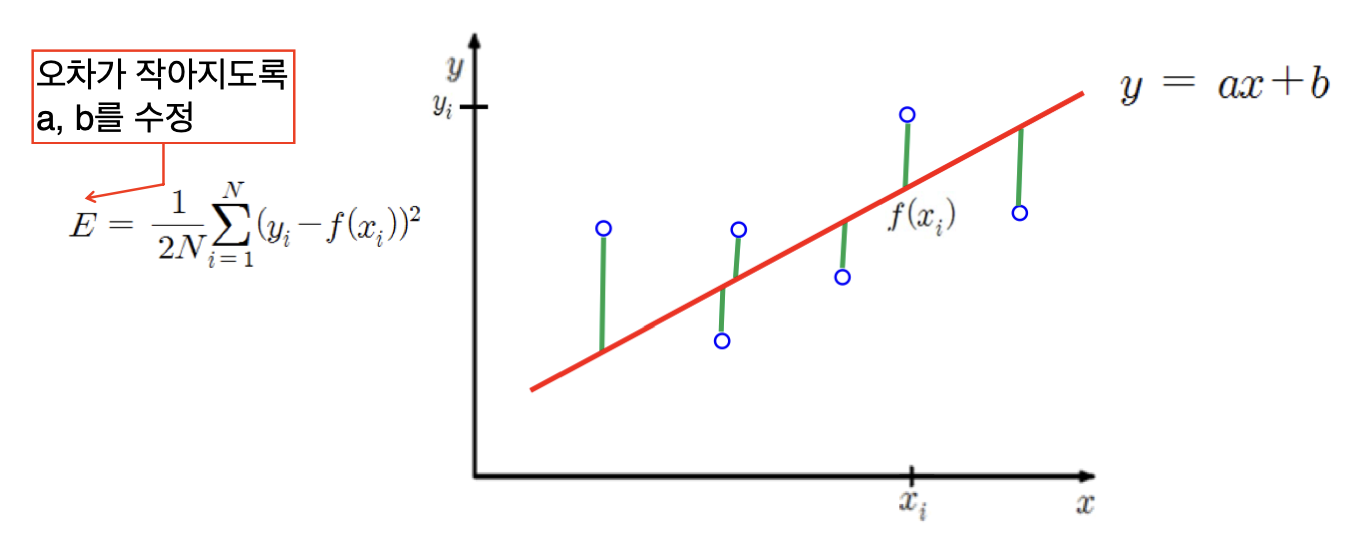
최소 평균제곱법을 사용해서 회귀(Regression) 문제의 최적함수를 찾거나,
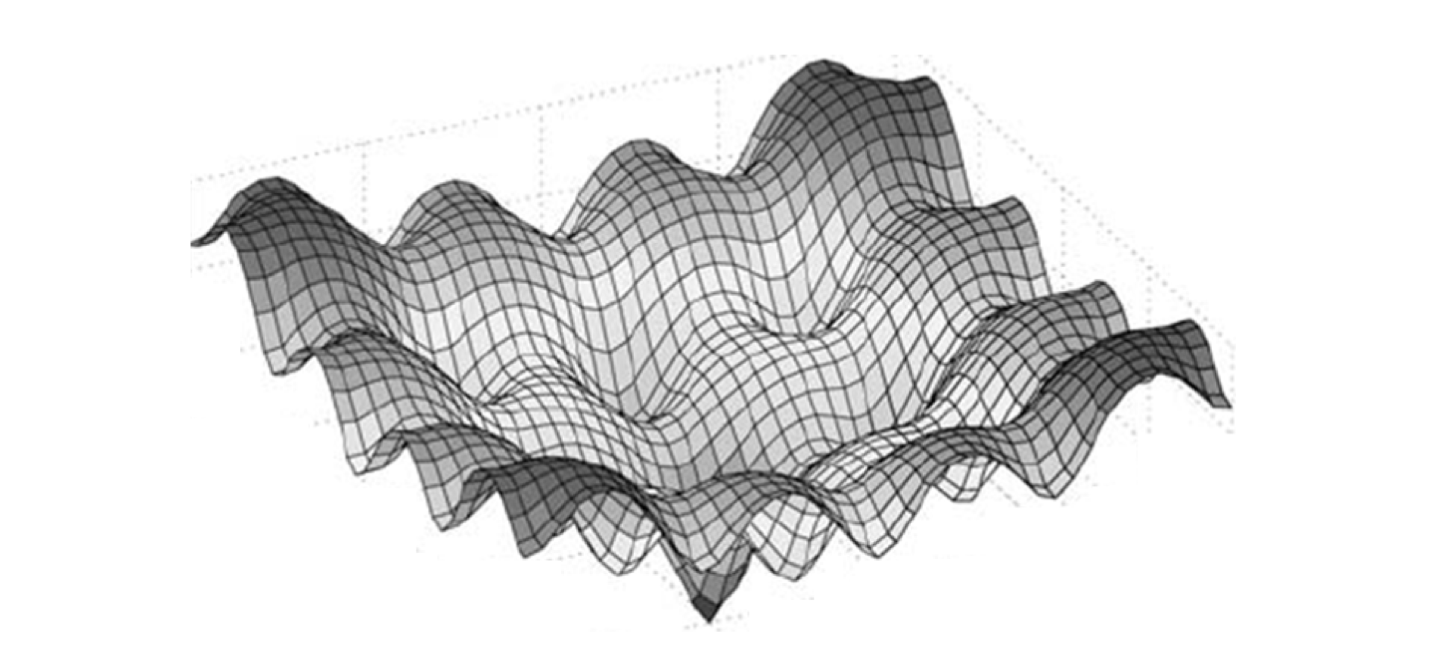
함수의 최소값 위치를 찾는 문제에서 경사 하강법과 같은 방법을 사용할 수 있다.