신경망
인공지능 신경망의 구조와 원리에 대해 알아봅니다.읽는데 6분 정도 걸려요.퍼셉트론
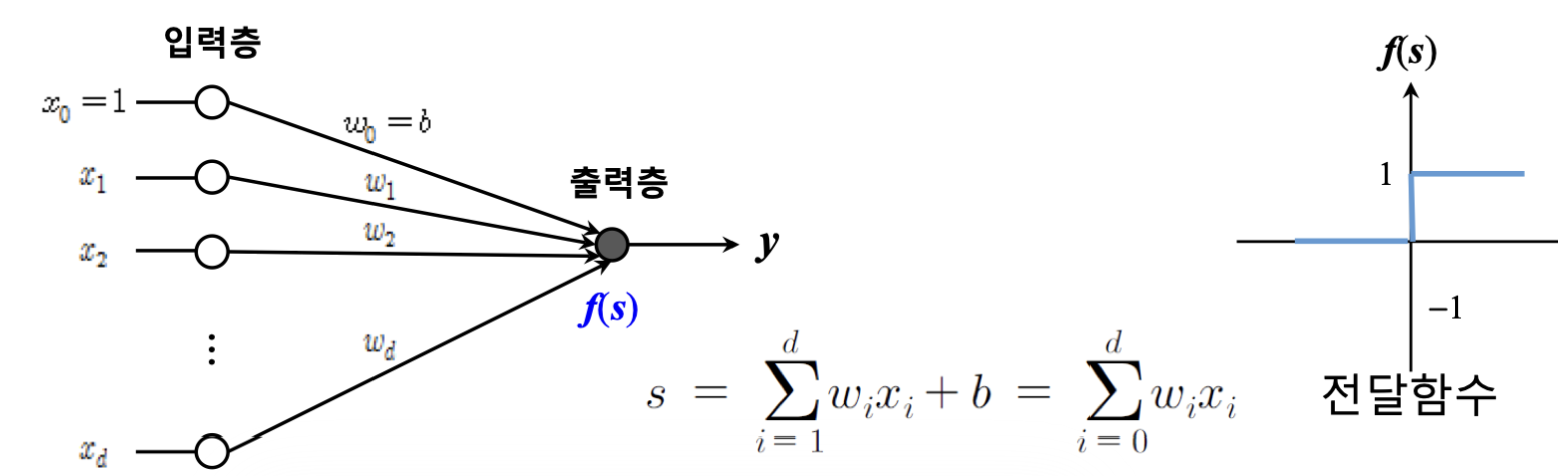
인간의 신경세포를 모방한 신경망 모델에서 하나의 신경세포에 해당하는 뉴런 유닛입니다.
다른 퍼셉트론의 출력들을 입력으로 받아 하나의 출력을 생성하게 되는데요, 입력들의 합이 threshold를 넘으면 1, 아니면 0을 출력하게 됩니다.
이 때, 부분을 아래와 같이 수정해봅시다.
threshold를 마찬가지로 하나의 입력으로 생각할 수도 있을 것입니다.
즉, 가중치(w)가 1이고, 값(x)이 bias 라고 생각하면 아래와 같이 식이 정리됩니다.
이제 s의 값이 0보다 작으면 0을 출력하고, 0보다 크면 1을 출력하면 퍼셉트론 완성입니다.
퍼셉트론을 이용해서 OR 회로를 만들어봅시다.
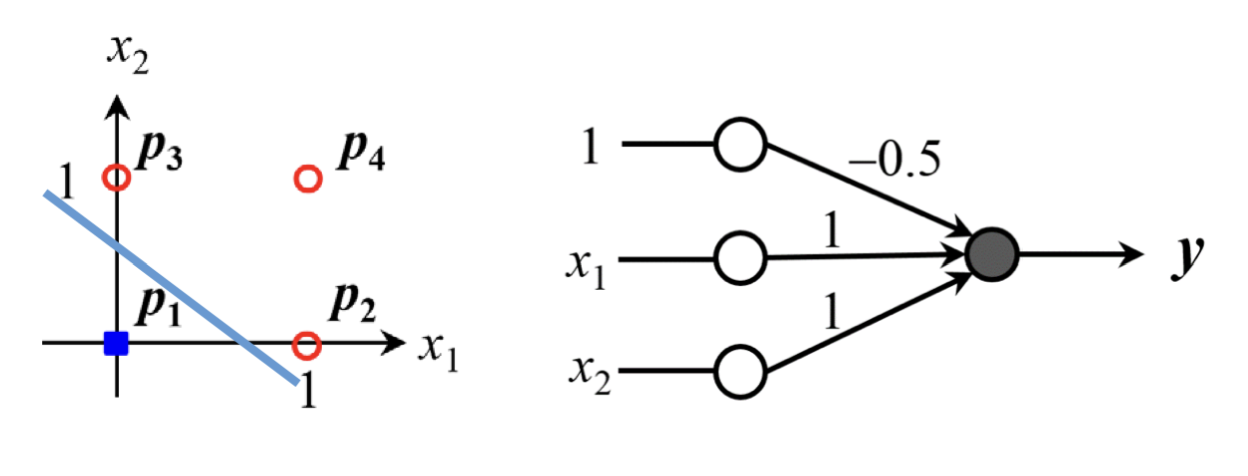
그럼 AND 회로는 만들 수 있을까요?
bias(1)에 연결된 weight에 -0.5가 아닌 -1.5와 같은 값을 넣으면 만들 수 있습니다.
그렇다면 XOR 회로는 만들 수 있을까요?
위와 같이 퍼셉트론 1개만으로는 구현이 불가능합니다.
하나의 퍼셉트론은 선형 분리가능 문제만 해결할 수 있기 때문입니다.
XOR와 같은 선형 분리불가 문제는 2개 이상의 퍼셉트론으로 해결할 수 있습니다.
다층 퍼셉트론
여러 개의 퍼셉트론을 층 구조로 구성한 신경망 모델을 의미하며, 이를 이용하면 단일 퍼셉트론의 한계였던 선형 분리불가 문제도 해결할 수 있습니다.
다층 퍼셉트론을 이용해서 XOR 회로를 만들어봅시다.
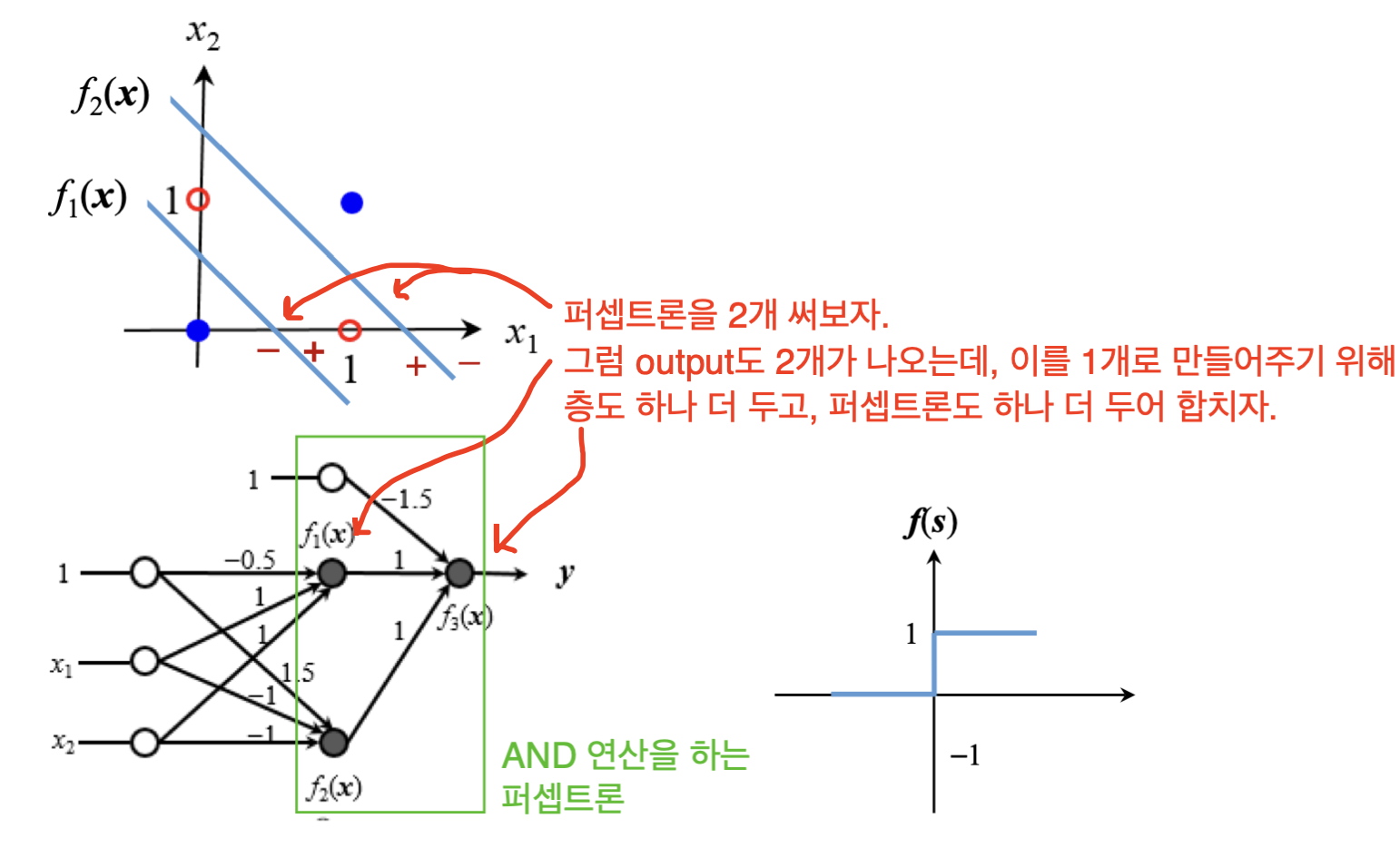
학습
다층 퍼셉트론을 학습을 시킨다는 것은 입력-출력 학습데이터에 대해 출력값과 오파의 차이가 최소가 되도록 가중치(weight)를 조정하는 것을 의미합니다.
이를 위해 역전파 알고리즘을 사용하는데, 역전파 알고리즘은 미분을 사용합니다.
따라서 수식화된 퍼셉트론이 미분 가능해야 하는데, threshold(bias)보다 크다/작다로 1/0이 나뉘는 step 함수를 사용하는 경우에는 미분이 불가능합니다.
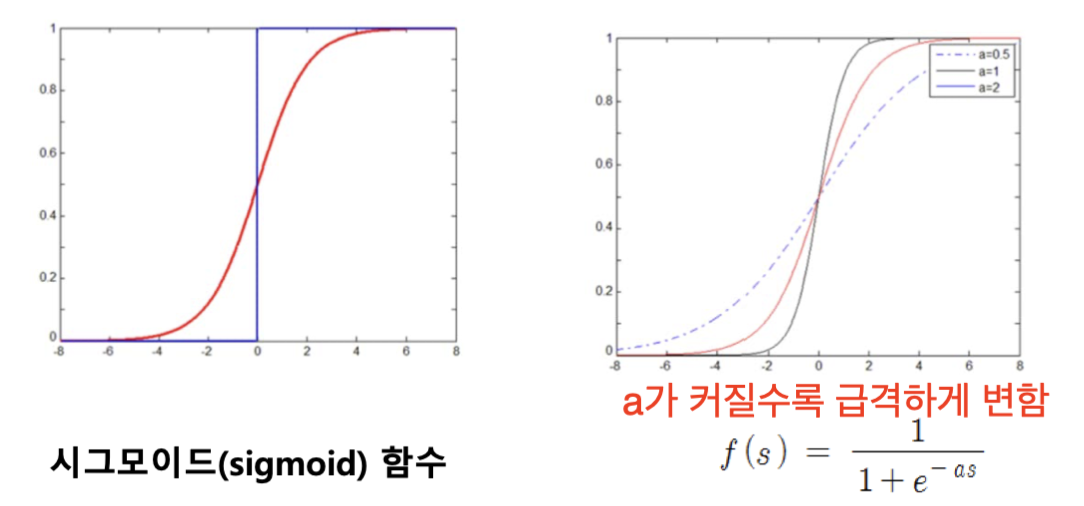
그렇기에 미분이 가능한 sigmoid 함수나 다른 함수를 사용하여 출력값을 결정합니다.
XOR와 같은 간단한 회로는 학습이 필요없이 바로 weight를 결정할 수 있지만, 사물 인식과 같이 상상할 수 없는 회로의 경우에는 퍼셉트론 층들을 많이 두고, 학습하는 방식으로 회로를 구성하게 됩니다.
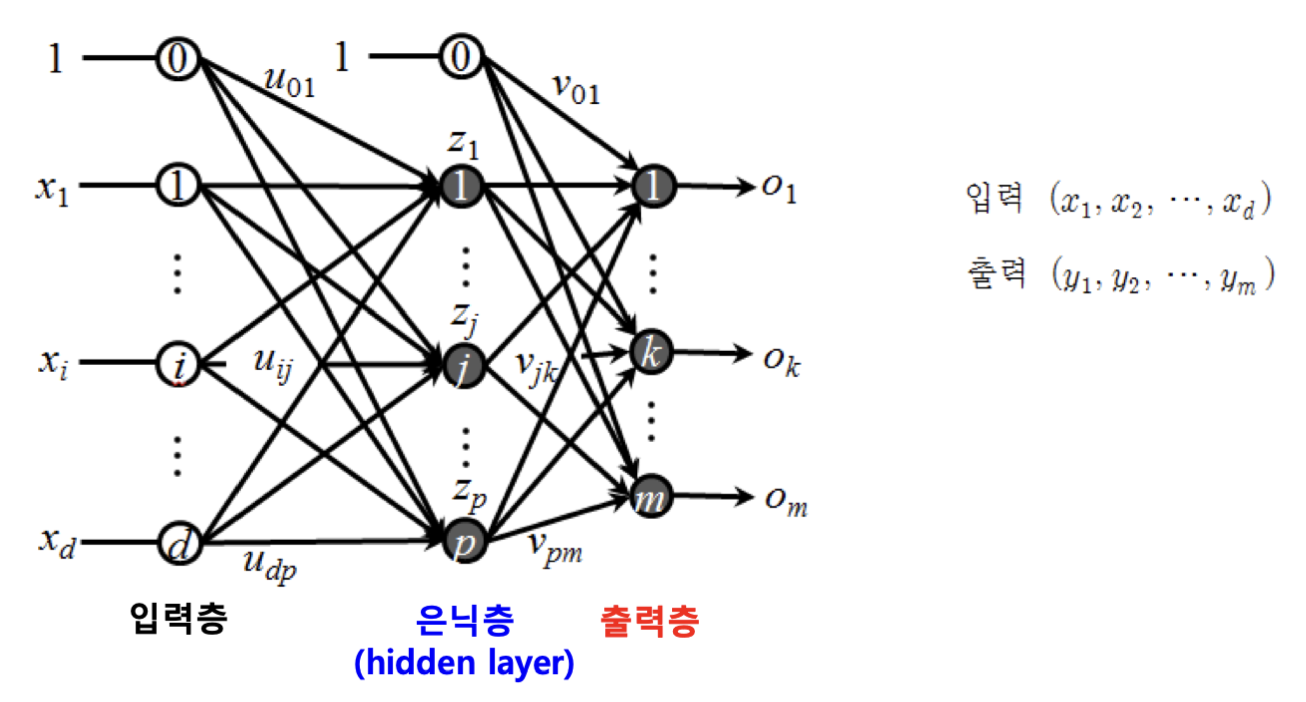
n개의 은닉층을 둔 n+1층 퍼셉트론을 구성하면 복잡한 회로도 만들 수 있습니다.
단, weight을 계산하는 것은 사실상 불가능하기 때문에 학습이라는 이름의 노가다(?)를 통해 weight이 오류가 적어지는 방향으로 조정하는 것입니다.
학습 데이터의 입력은 들의 벡터로 주어지고, 출력은 의 벡터로 주어지는데, 중 하나만 1이고 나머지는 0인 ont-hot 벡터로 주어지는게 일반적입니다.
오류를 줄이는 방향으로 학습하기 위한 방식으로 최대경사법 또는 경사하강법이라는 태크닉이 사용됩니다.
원리만 설명하면, 각 스탭에서의 x, y 편미분을 구합니다(gradient).
그리고, gradient의 반대 방향으로 weight를 수정하면 에러가 작아지는 방식입니다.
기타
최종 출력시 모든 속성값에 대한 확률을 0~1로 표현하기 위해 마지막 층으로 소프트맥스 층을 두기도 합니다.
소프트맥스 층은 최종 출력을 분류 확률로 변환하는 층으로 모든 퍼셉트론 출력의 합이 1이 됩니다.
가중치를 사용하는 대신, 퍼셉트론이 기존 벡터와 입력 벡터의 유사도를 측정하는 방식인 RBF망 이라는 방식도 있습니다.