웅덩이

이미지 훼손은 아래와 같은 공식에 의해 이루어졌다는 가정하에 진행됩니다.
따라서 현실 세계의 훼손을 복원할 때는 제대로 동작하지 않습니다.

g(x,y) = h(x,y) * f(x,y) + \eta(x,y)

$h$ : 훼손 함수
$\eta$ : 노이즈

즉, 이미지를 복원시킨다는 것은 훼손된 영상 $g$ 에 대해 $h$ 와 $\eta$ 를 알고 있을 때, 그 영향을 제거하는 방향으로 진행합니다.

Noise Restoration

우선 영상의 노이즈를 줄이는 방식을 알아보겠습니다.

Noise Model

노이즈를 줄이기 위해서는 노이즈가 어떻게 생겼는지 분석할 필요가 있습니다.
100%는 아니지만, 자연계에서 노이즈가 발생하는 방식은 여러 방식으로 모델링하여 추상화 할 수 있지만, 그 중에 대표적인 노이즈 모델에 대해서만 알아보겠습니다.

Gaussian Noise

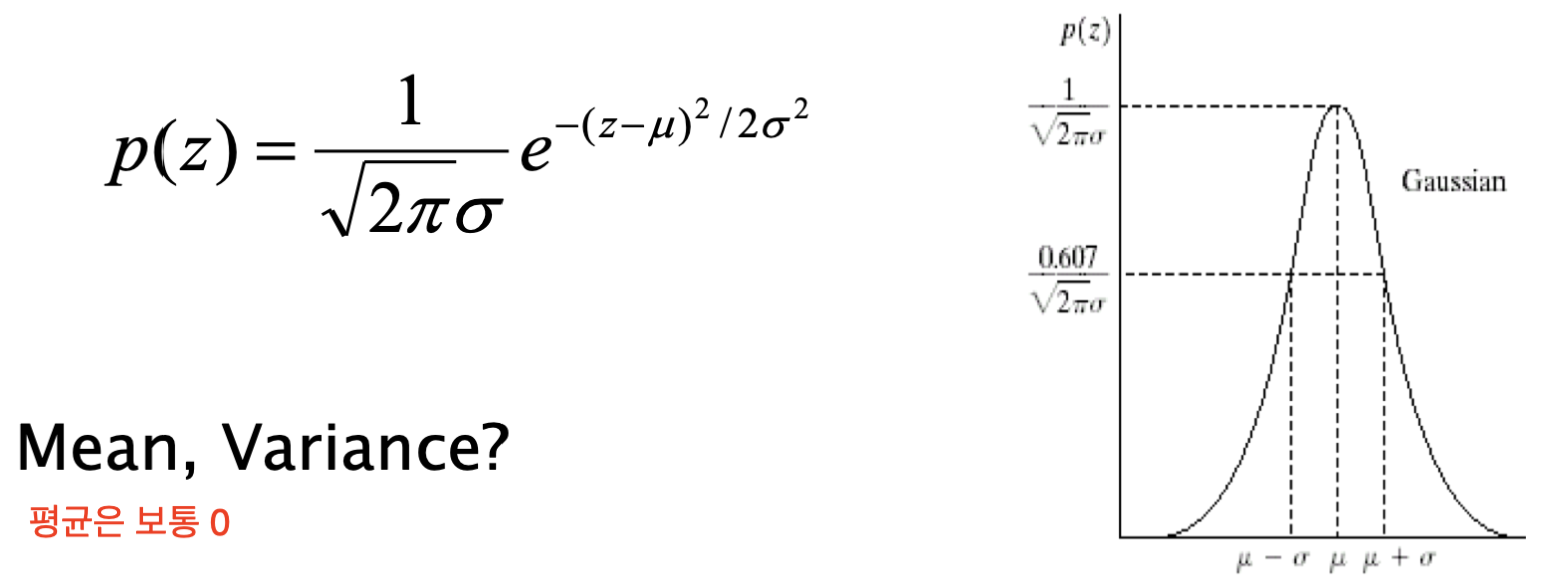
Gaussian Noise는 말 그대로 가우시안 분포를 따르는 노이즈 패턴으로 자연계에서 발견할 수 있는 형태를 갖습니다.
Uniform Noise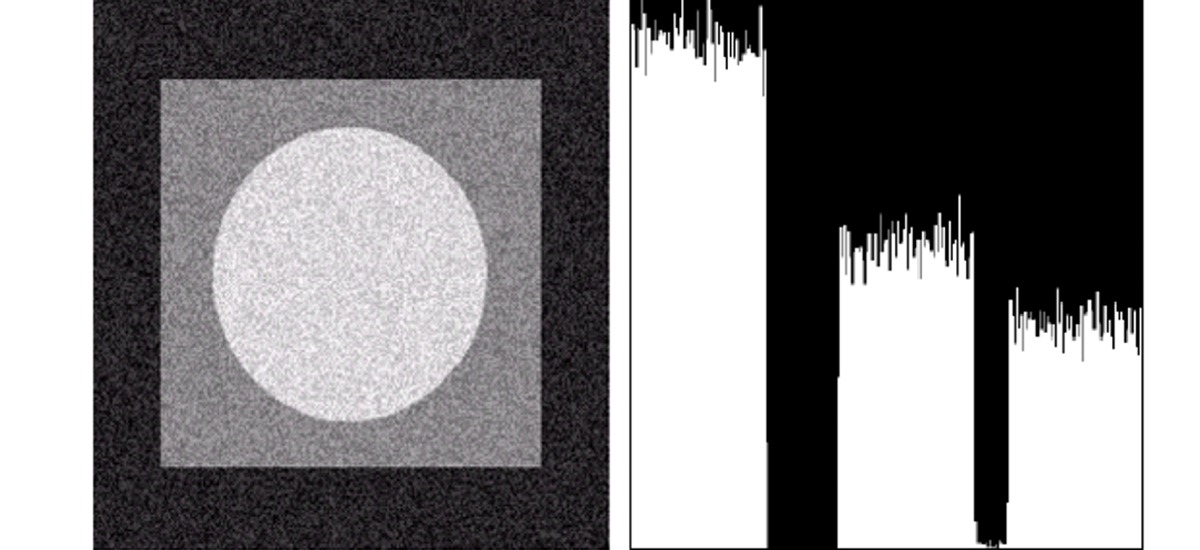

Uniform Noise는 동일한 확률 분포로 노이즈 패턴을 갖는 형태입니다.
Impulse (Salt-and-Pepper) Noise

$p(z) = \left\{\begin{matrix} P_a \; for \; z=a \\ P_b \; for \; z=b \\ 0 \; otherwise\end{matrix}\right.$
Salt-and-Pepper Noise는 일정 확률로 0 또는 255로 노이즈가 생기는 형태입니다.

Mean filter

Mean filter는 간단하게 말해서 기존에 많이 써왔던 smoothing filter와 동일합니다.
직역하면 평균값 필터 입니다.

\hat{f}(x,y) = \frac{1}{mn} \sum_{(s,t)\in S_{xy}}^{} g(s,t)

즉, 전체적인 노이즈를 뿌옇게 만듦으로서 노이즈를 줄이는 것이기에 가우시안 노이즈에 효과적 입니다.
하지만, 영상의 디테일이 뭉게진다는 한계가 존재합니다.

Median filter

Median filter는 간단하게 말하면 특정 윈도우 $S$ 내부의 값을 일렬로 정렬했을 때 가운데 값으로 대체하는 필터입니다.
직역하면 중앙값 필터 입니다.

\hat{f}(x,y) = \underset{(s,t)\in S_{xy}}{median} \{g(s,t)\}

즉, 0, 255와 같은 특이값을 중앙값으로 대체할 수 있기 때문에 Salt-and-Pepper 노이즈에 효과적 입니다.
하지만, 특정 윈도우 영역에 노이즈가 우연히 많이 분포하게 될 경우 복원이 불가능 합니다.

Adaptive Mean filter

Adaptive filter는 기존 필터와 다르게 영상의 특징을 반영하여 영역별로 다르게 필터링을 한다는 특징이 있습니다.

\hat{f}(x,y) = g(x,y) - \frac{\sigma_\eta^2}{\sigma_L^2} (g(x,y) - m_L)

이 수식을 자세히 분석해봅시다.

$\sigma_\eta^2$ 가 0 이라는 뜻은 노이즈의 분산이 0이라는 뜻입니다. 즉, 노이즈가 없다는 뜻입니다.
이 때의 위 수식의 좌변은 $g(x,y)$ 만 남게 됩니다.
즉, 노이즈가 없는 영상은 별 다른 변환 없이 통과하게 됩니다.

$\sigma_L^2$ 가 $\sigma_\eta^2$ 에 비해 매우 높은 경우는?
노이즈의 분산에 비해 영상 자체의 분산이 매우 크다는 의미입니다.
즉, 영상의 변화율이 크기 때문에 디테일을 살리기 위해 필터( $m_L$ )의 강도를 매우 약하게 설정해야 한다는 의미입니다.
실제로 $\sigma_\eta^2$ / $\sigma_L^2$ 를 0.1과 같은 작은 값을 넣고 계산하면 필터의 영향력이 10%만 발휘된 변환 영상을 얻을 수 있습니다.

$\sigma_L^2$ 가 $\sigma_\eta^2$ 와 같은 경우는?
노이즈의 분산이 원본영상 + 노이즈의 분산과 같다는 의미입니다.
즉, 영상의 변화율이 없다는 의미이므로, 필터를 강하게 해서 디테일을 뭉게도 영향이 없는 상태입니다.
실제로 $\sigma_\eta^2$ / $\sigma_L^2$ 에 1을 넣고 계산하면 100% 필터링된 변환 영상을 얻을 수 있습니다.

이렇듯, 노이즈의 분산( $\sigma_\eta^2$ )과 원본영상 + 노이즈의 분산( $\sigma_L^2$ )을 비교하여 필터( $m_L$ )링 강도를 결정하면, 디테일이 필요한 부분은 필터링을 약하게, 디테일이 필요없는 부분은 필터링을 강하게 하여 노이즈를 줄일 수 있습니다.

Adaptive Median filter

이 경우엔 수식이 아닌, 일련의 명령어 집합으로 소개가 되어있기에 일단 소개하고 한 줄 한 줄 분석해보도록 하겠습니다.

231125-163400

Line 1~3
median이 min, max가 아닌 값이 있다?
→ 주변에 salt, pepper도 있고, 원본 영상도 섞여있다.
→ B에서 후 처리.

Line 4~6
median이 min, max값 중 하나라면 해당 부분이 salt, pepper인지, 아니면 원본 영상 자체가 0, 255 값을 갖는건지 알 수 없다.
→ 윈도우 사이즈( $S_{xy}$ )를 키워서 A 재시도.

Line 7~9
픽셀 값이 min, max가 아니다?
→ 노이즈가 아니고 원본 값이다.
→ 원본 영상 그대로 리턴.

Line 10
픽셀 값이 min, max값 중 하나라면 해당 부분은 salt, pepper 노이즈일 것.
→ 중앙값 리턴.

Degradation Restoration

Estimating the Degradation Function

이제 노이즈는 어느정도 제거했다고 가정하고, 훼손 함수 $h$ 를 추정하는 법을 알아봅시다.
추정만 해낼 수 있다면 이를 역으로 연산하는 과정을 통해서 제거할 수 있기 때문에 추정하는 대표적인 3가지 방식에 대해 알아봅시다.

Observation

부분의 H는 전체의 H와 같기 때문에 부분을 잘 선택하고, 노가다(?)를 통한 원본 영상을 만들어내어 그 변환과정(H)을 얻을 수 있다면, 전체 영상에 대한 복원이 가능해집니다.
Experimentation

impulse에 대한 H의 response를 보면 그 변환과정(H)을 얻을 수 있습니다.
Mathematical modeling

Inverse filter

이제 찾아낸 훼손 함수 H를 기반으로 복원을 해봅시다.
그 전에 앞서 가정했던 이미지 훼손 공식을 푸리에 변환한 식을 살펴봅시다.

G(u,v) = F(u,v)H(u,v) + N(u,v)

노이즈(N)는 앞에서 많이 줄였기에 없다고 가정했을 때 우리가 복원해야 하는 원본 영상 F는 다음과 같이 정의할 수 있습니다.

\hat{F}(u,v) = \frac{G(u,v)}{H(u,v)} = F(u,v) + \frac{N(u,v)}{H(u,v)}

복원이 완벽하게 이뤄질 수는 없기에 $\hat{F}$ 의 형태로 표현하였습니다.
이 식에서 $\frac{N(u,v)}{H(u,v)}$ 부분을 유심히 살펴봅시다.

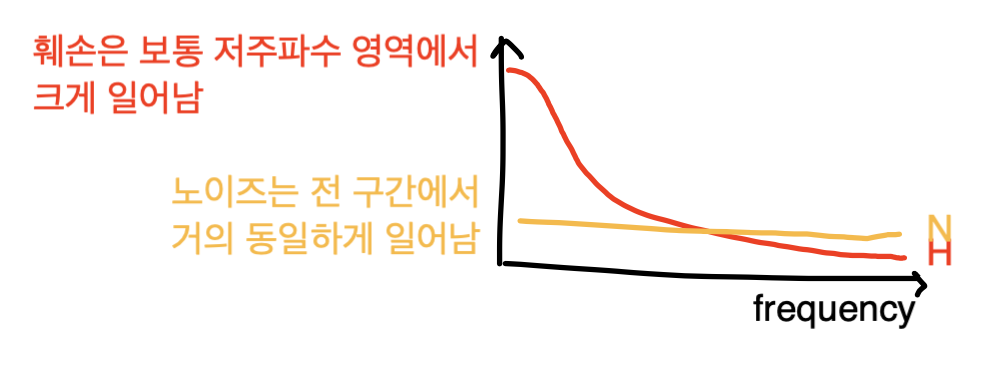
231125-165953

보통 노이즈는 모든 주파수 구간에서 동일하게 일어납니다.
하지만, 훼손은 보통 저주파수 영역에서 크게 일어나는 특징이 있습니다. (그렇다네요)

따라서 고주파수 영역에서는 $\frac{N(u,v)}{H(u,v)}$ 값이 매우 커지는,
즉, 노이즈가 부스트되는 현상이 발생하게 됩니다.

231125-170139

따라서 훼손을 줄이는 과정에서 적당히 lowpass 를 해주는 것이 영상 품질을 높이는데 도움이 될 수 있습니다.