웅덩이

Fourier Transform

푸리에 변환을 간단하게 말하면 시간, 공간 도메인의 주기를 갖는 사인파의 합을 주파수 도메인의 함수로의 변환을 말한다.

도메인 간의 관계

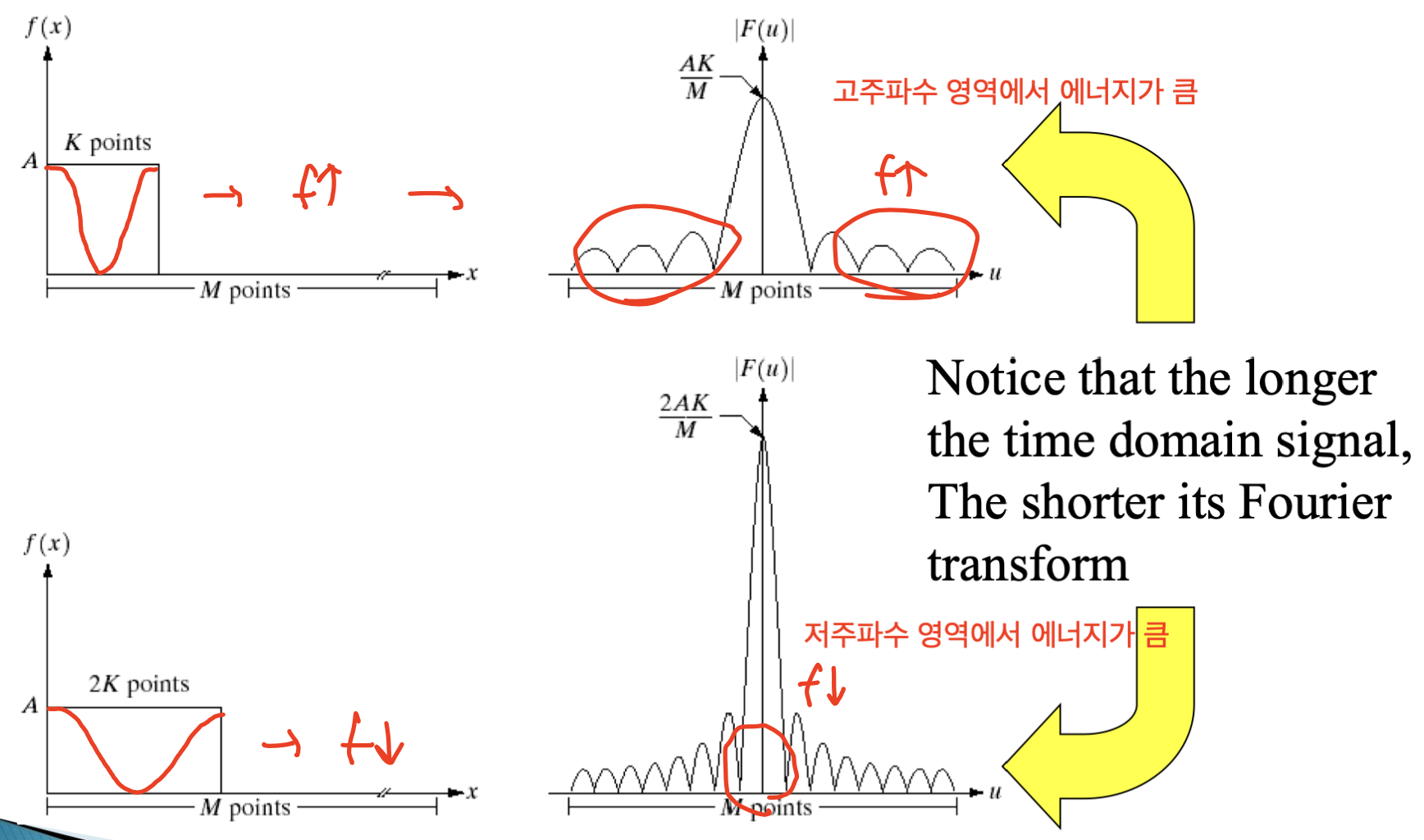
231018-211849

시간 도메인이 길다는 의미는 주파수가 낮다는 뜻이다.
따라서 푸리에 변환시 저주파수 영역에서 값이 크게 나타난다.
반대의 경우도 마찬가지.

전에 헷갈렸던 내용으로 다시 돌아가서 보면 이해될 것.

Property

이제 영상을 푸리에 변환을 통해 주파수 도메인으로 변화를 시킬건데, 그 결과물을 분석하는 법을 알아보자.

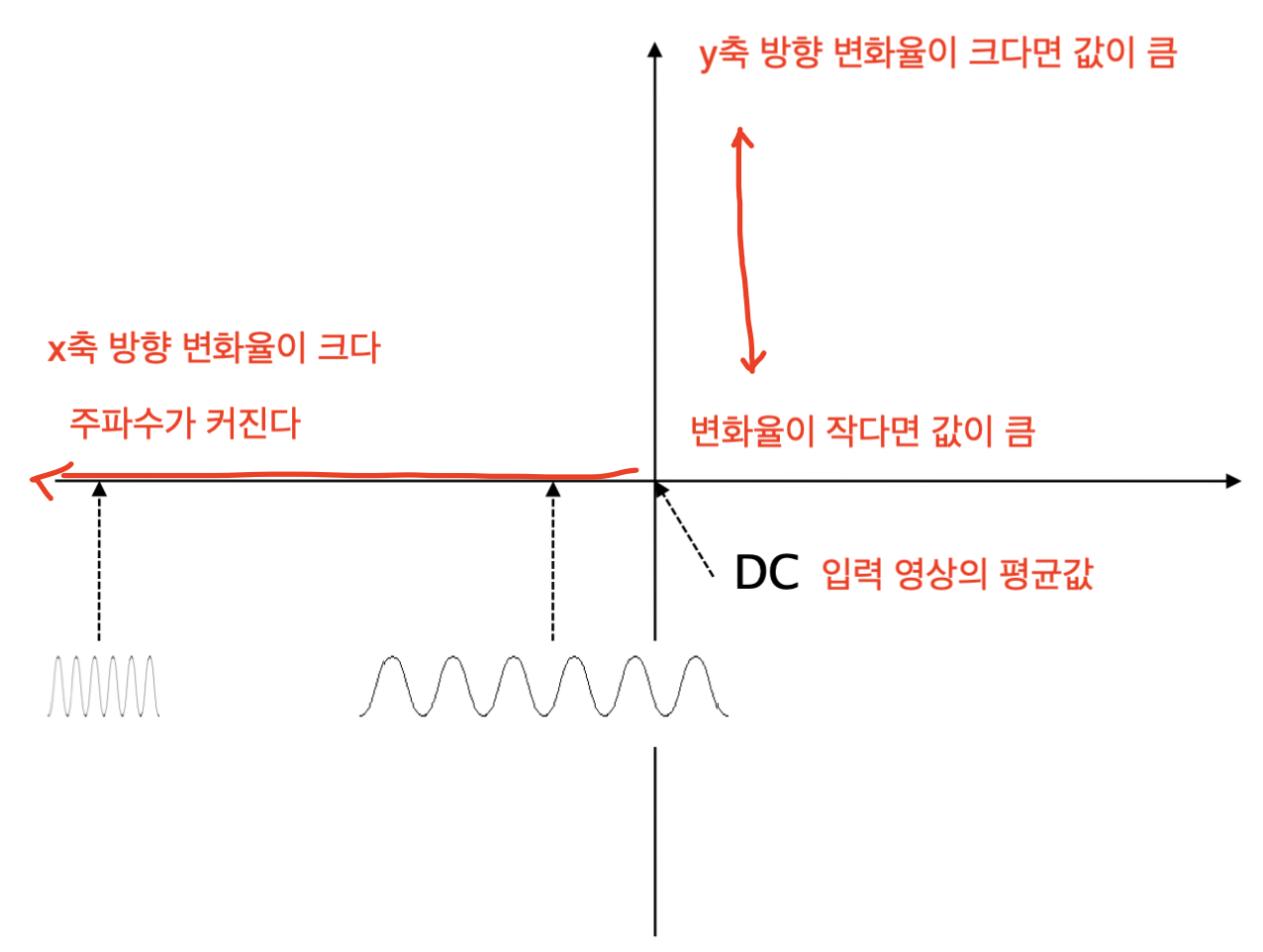
231018-212424

DC, 즉, 원점에 가까워 질 수록 주파수가 낮은 영역, 멀 수록 주파수가 높은 영역을 나타내는데,
영상에서의 주파수는 변화율이라고 보면 된다.
즉, 주파수가 크다 라는 의미는 영상이 변화하는 부분이 많다는 뜻이다.

231018-213206

이 변환결과를 보고 이해해보자.

우선 주파수 데이터를 보면 먼 곳이 어둡다.
즉 영상 전체적으로 확확 변하는 부분이 적다는 뜻이다.

그런데 X 모양으로는 밝은 것을 볼 수 있다.
이 뜻은 해당 방향과 수직한 방향으로 변화가 많다는 것을 의미한다.
실제로 원본 영상을 보면 같은 방향으로 홈도 파져있고, 변화가 많은 모습을 확인할 수 있다.

그리고 미세하게 세로 방향으로 점선과 같은 무늬가 있다.
이는 원본 영상에서 가로 방향으로 긴 무언가가 변화가 큼을 의미한다.
실제로 원본 영상에는 가로로 흰 실같은 무언가가 있다.

마지막으로 주파스 데이터 전체적으로 노이즈가 있다.
이는 원본 영상에서도 노이즈가 있다는 뜻이다.

Frequency Domain Filtering

이제 푸리에 변환을 이용해서 주파수 도메인으로 변환된 영상을 이용한 필터링을 해보자.

이 것이 가능한 이유는 LTI System 이기에 가능한 것이다.
LTI System과 푸리에 변환을 이용한 연산의 단순화에 대한 내용은 여기에서 확인하자.

231018-214840

앞으로 살펴볼 필터링에 대해 이 영상과 주파수 영상을 사용할 예정이다.
여기서 주파수 영상의 얇은 흰 원 부분은 무시하자.
일종의 $D_0$ 로 반지름을 나타내는 것인데, 원본 영상을 푸리에 변환 할 경우에는 나오지 않는다.

Ideal Lowpass Filter

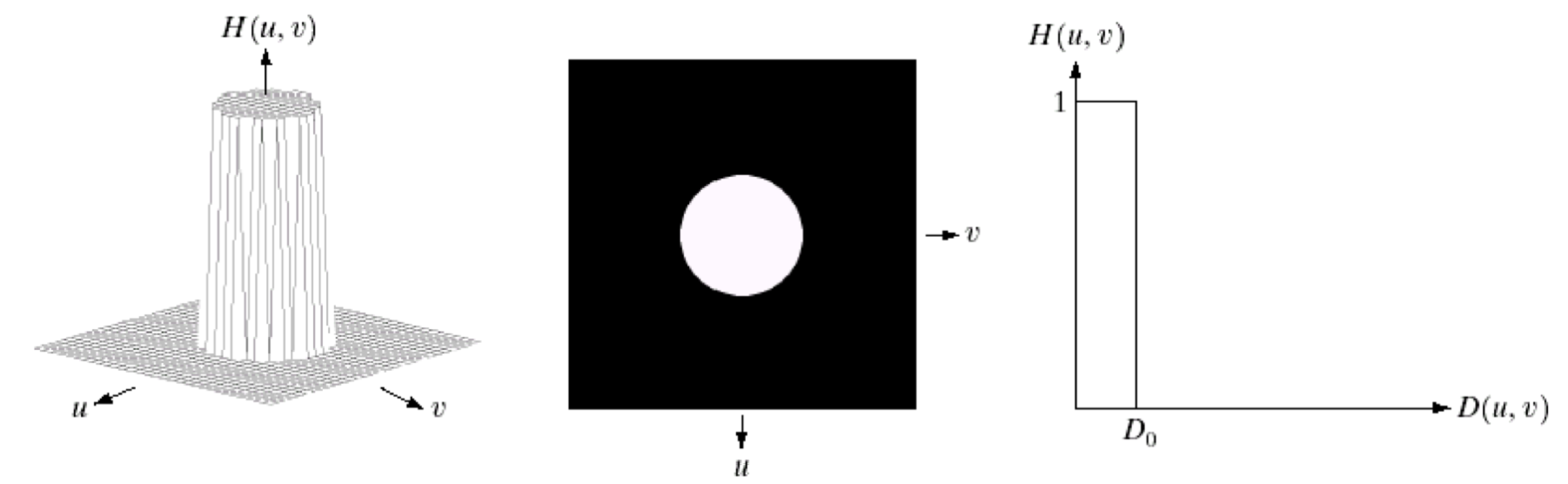
231018-214145

원본 영상을 푸리에 변환을 하고, 그 주파수 영상에 대해 위 사진의 흰색 영역만 살리고 나머지는 검게 만든 후 다시 역 푸리에 변환을 해볼 것이다.
이 때, 위의 흰색 영역을 보면 낮은 주파수 영역만을 통과시킴을 알 수 있다.
즉, 고주파수 영역, 변화량이 많은 영역을 없앤다는 뜻인데, 변화량이 많은 영역을 없앤다?
즉, 영상을 뿌옇게 만들어 변화량이 적어지도록 하겠다는 의미이다.

정리하면 Lowpass filter를 통과시키면 영상 전반적으로 Smoothing filter처리를 한 결과를 얻을 수 있다.

해당 주파수 필터는 다음과 같이 정의할 수 있는데,

H(u,v) = \left\{\begin{matrix} 1 \;\; if \;\; D(u,v) \leq D_0 \\ 0 \;\; if \;\; D(u,v) > D_0 \end{matrix}\right.

이렇게 이상적으로 0과 1이 나뉘는 필터를 Ideal Lowpass filter라고 부른다.

231018-215052

상단부터 지그재그 모양으로 $D_0$ 가 5, 15, 30, 80, 230 값으로 통과시키는 주파수 대역을 점점 늘린 변환 결과이다.

$D_0$ = 5, 즉 매우 낮은 주파수를 갖는 대역만 통과시킨 영상은 영상이 매우 Smoothing 처리된 것을 확인할 수 있다.
이게 무슨 의미냐면 그정도의 낮은 변화율로는 원본 영상의 가파른 변화를 표현하지 못하고,
변환된 영상 정도의 완만한 변화율만 표현 가능하다는 뜻이다.

따라서 $D_0$ 의 값을 키울수록 높은 변화도 표현 가능해져 점점 영상이 선명해지는 것을 볼 수 있다.
다르게 말하면 $D_0$ 값이 클수록 필터링 강도가 약해진다.

이때 주의깊게 볼 점은 변환된 영상에서 뭔가 일렁이는 듯한 노이즈가 생겼다는 점이다.
왜 이런게 생긴걸까?

바로 Ideal filter 특성 때문에 고주파수 영역을 깔끔하게 날려버렸기 때문에 세밀한 변화를 묘사하지 못해 화질이 떨어진 것이다.
이를 개선할 수 없을까?

Butterworth Lowpass Filter

'가능.' 당연히 개선할 수 있다.
주파수 영역을 필터링할 때 적절하게 고주파수 영역을 통과시킨다면 화질 개선이 가능한데, 그 방법이 Butterworth 방식이다.

231018-215943

약간의 곡률을 추가함으로서 일부 고주파수 영역을 통과시킨다.
이 그래프를 구현하는 식은 다음과 같이 생겼다.

H(u,v) = \frac{1}{1+[D(u,v) / D_0]^{2n}}

실제로 개선이 되었을까?

231018-220523

Smoothing 효과는 살짝 약해졌지만, 확실이 울렁이는 듯한 노이즈는 제거되었다.
약간의 화질 개선이 이루어 진 것이다.

Gaussian Lowpass Filter

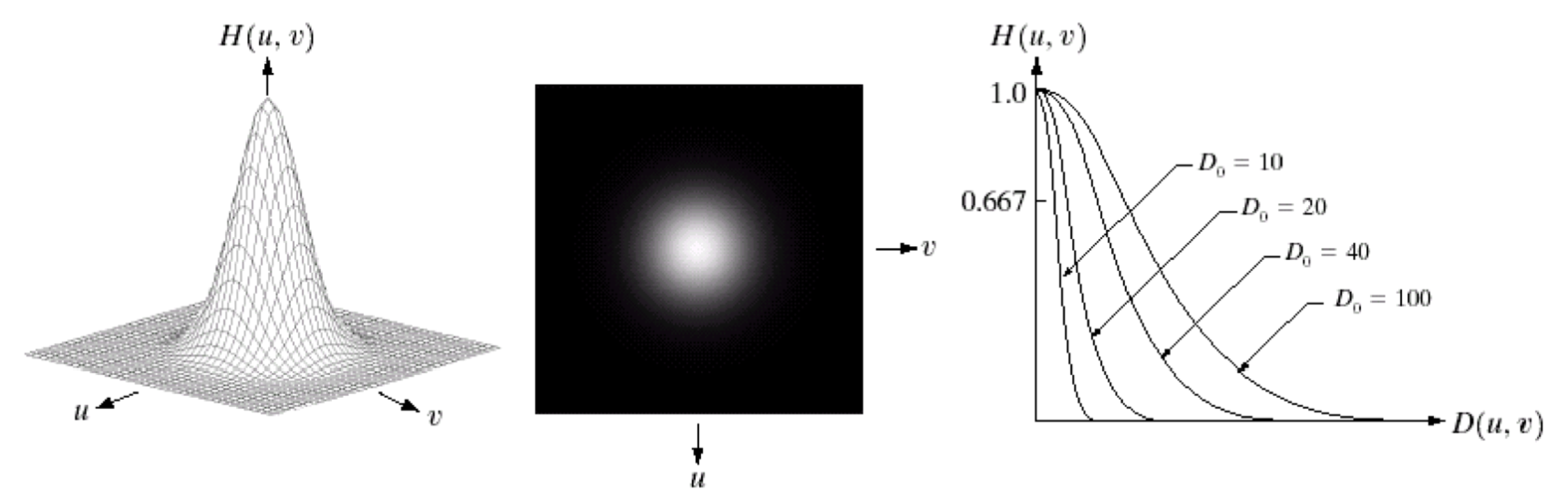
231018-220657

H(u,v) = e^{-D^2(u,v)/2D_0^2}

위에 두 필터보다 성능이 좋은 가우시안 필터도 있다.
그런데 Butterworth와 육안으로 구별되는 정도는 아니다.

Highpass Filter

Lowpass는 영상을 뿌옇게 만들었는데, 반대로 Highpass는?
그렇다. 영상을 더 샤프하게 만든다.
정확하게 말하면 변화가 큰 부분만을 남기기에 Laplacian filter와 유사한 기능을 수행한다.

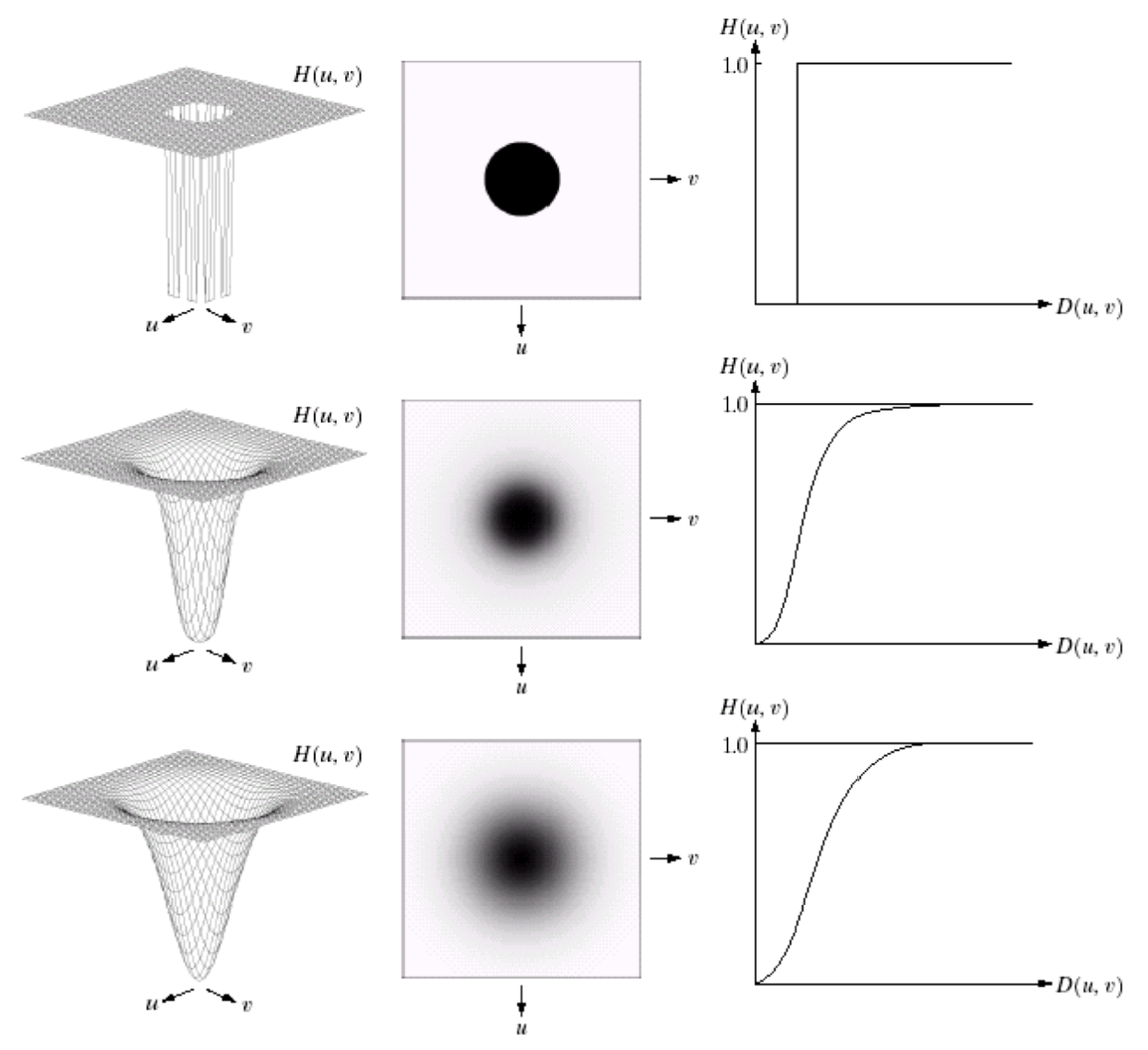
231018-221102

위에서 부터 차례대로 Ideal, Butterworth, Gaussian Highpass Filter이다.
함수를 구하는 방법은 그저 1에서 Lowpass 함수를 빼주면 된다.
(Butterworth의 경우에는 $D$ (분모) 와 $D_0$ (분자)의 위치를 변환하면 된다)

231018-221329

Ideal Highpass의 결과이다.
역시 $D_0$ 값을 키울수록 필터의 강도가 약해진다.
그렇기에 노이즈 역시 줄어든다.

231018-221426

같은 필터 강도의 결과이다. 왼쪽부터 차례대로 Ideal, Butterworth, Gaussian Highpass이다.
이번엔 Butterworth와 Gaussian도 육안으로 차이가 난다.
여기서도 마찬가지로 Gaussian filter가 노이즈가 없고 깔끔하다.