Image Transform and RANSAC
영상을 변환하는 방법을 알아봅니다.읽는데 6분 정도 걸려요.영상을 변환하는 방법은 가상세계 - Matrix and Transformations에서 소개했었습니다.
이제 영상이 주어졌을 때 어떻게 위 변환식을 도출하는지에 대한 과정을 살펴보겠습니다.
Transformation Fitting
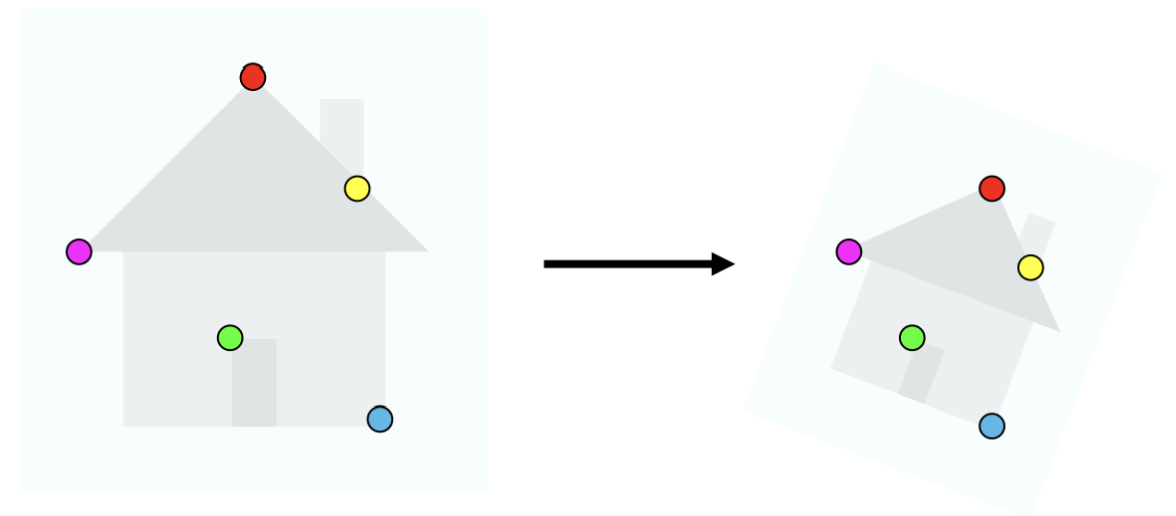
영상이 위와 같이 변환된다고 가정해봅시다.
이 때 위의 식에서 하나의 특징점은 아래와 같은 식을 통해 변환된다고 할 수 있습니다.
식은 2개, 모르는 미지수는 6개.
즉, 3개의 점에 대한 변환식을 구하면 6개의 미지수(, , )를 모두 구할 수 있습니다.
여기서 위 식을 아래와 같이 변환할 수 있는데요,
특징점 변환식 하나 당 ... 부분에 식이 들어갑니다.
위 식을 라고 합시다.
그렇다면, 특징점이 5개라면 식이 10개가 만들어져 은 10by6 행렬이 만들어지는 것이죠.
참고로, 최소 3개가 필요한 것이고, 더 많은 특징점을 사용한다면 에 대한 오차를 선형대수학을 이용하여 줄일 수 있습니다.
이제 양변에 를 취해준다면, 를 사용하여 미지수 6개를 얻을 수 있습니다.
RANSAC
위의 선형대수학 방식을 이용하여 특징점이 변환되는 pair를 선으로 연결하여 시각화 하면 아래와 같은 모습을 보입니다.

대부분은 맞지만, 몇몇 outlier가 있습니다.
이런 outlier 때문에 선형 변환 P에 오차가 생기기 마련인데요, RANSAC은 이런 outlier를 빼고 예측할 수 있는 방법을 제공합니다.
RANSAC은 아래의 방식을 통해 outlier의 영항을 제거하고, inlier로만 예측하도록 도와줍니다.
-
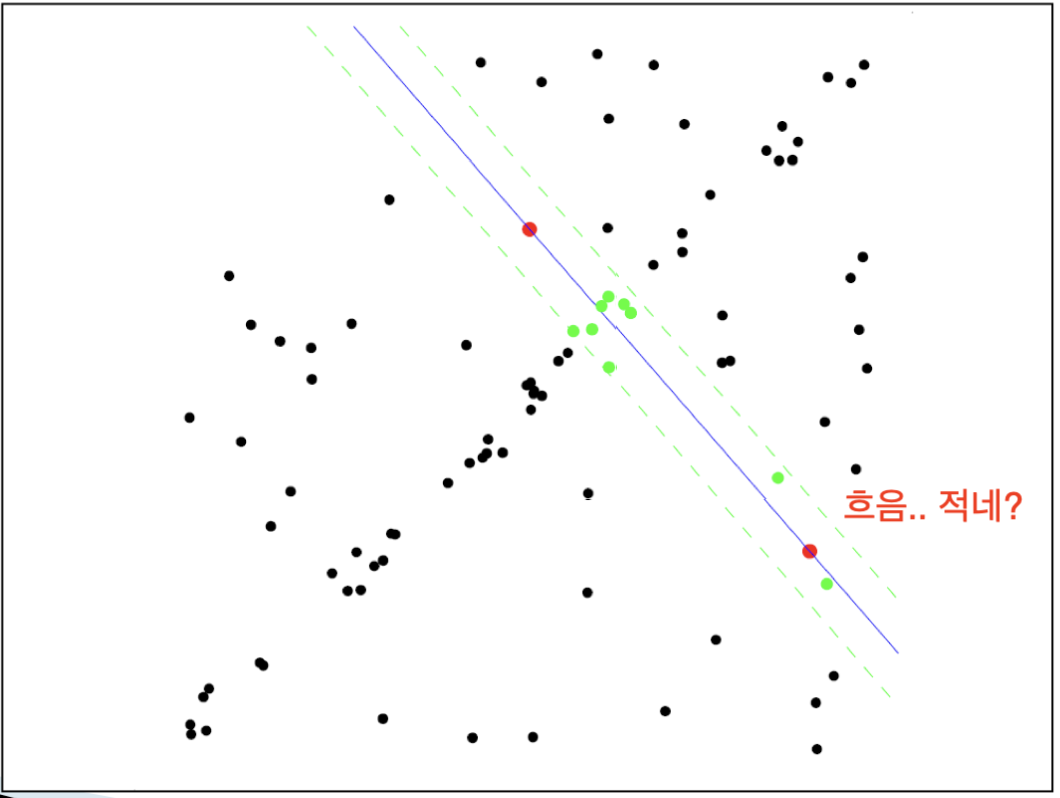
랜덤으로 특징점을 선택한다.
운이 좋다면 피팅이 잘 될 것이고, 운이 좋지 않다면 잘 안될 것이다.참고로, 좋은 피팅의 경우에는 랜덤 선택되지 않은 특징점에 대해서도 에러가 작을 것이고, outlier에 대해서만 에러가 클 것이다.
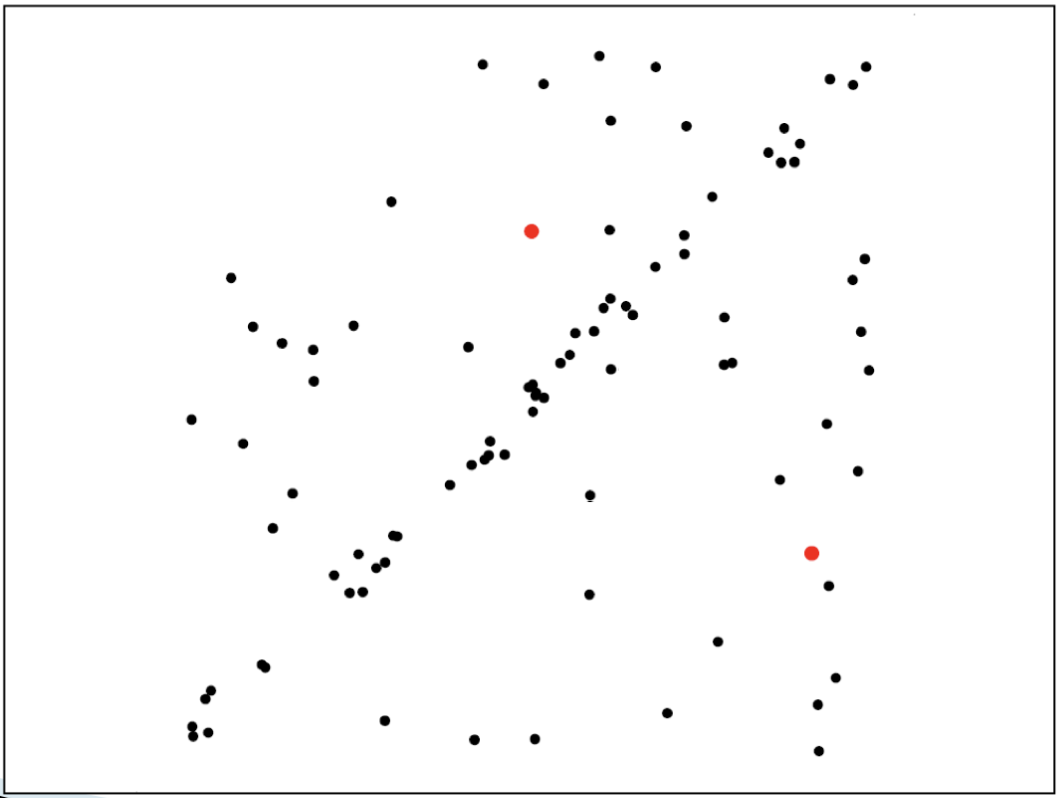
-
렌담으로 선택된 특징점을 이용해서 Transformation을 구한다.
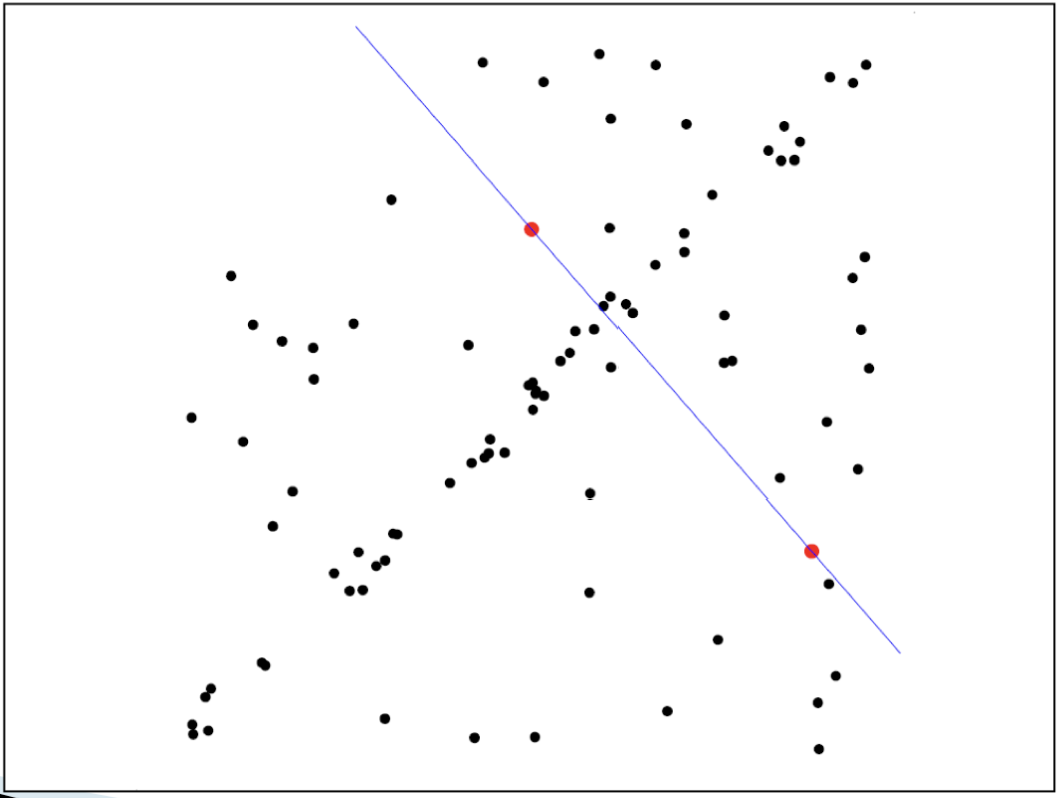
-
구한 Transform(P)에 대해서 에러를 계산하여 inlier를 찾아본다.
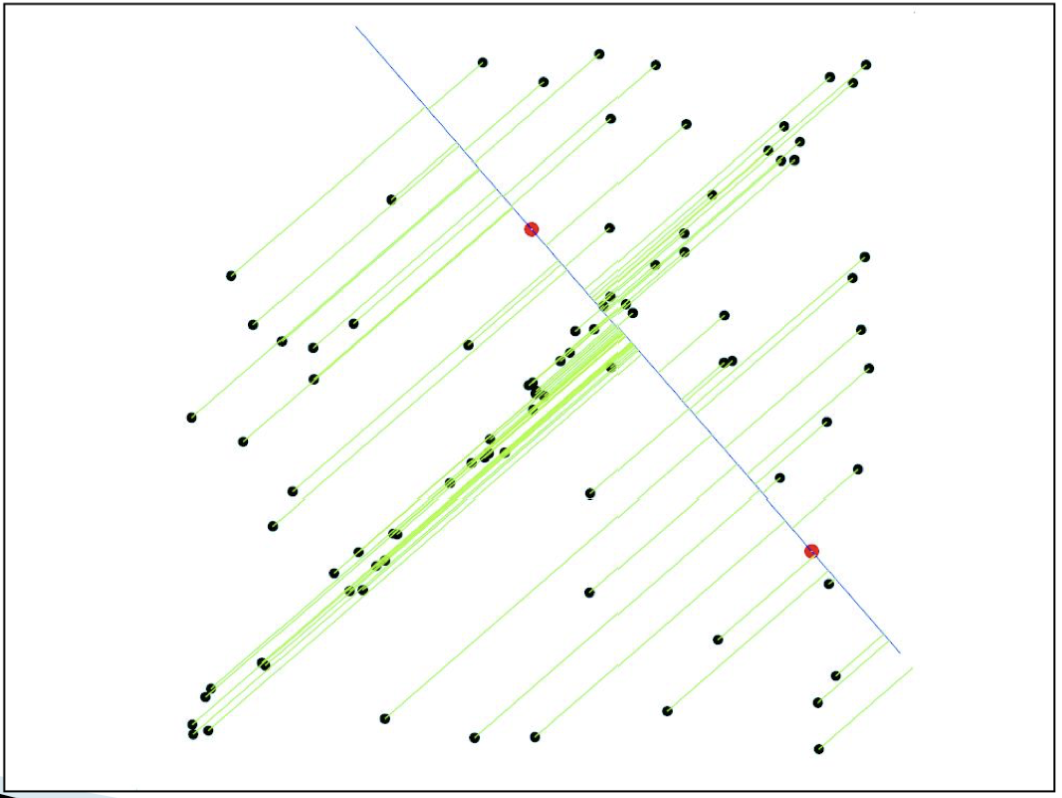
-
inlier의 개수가 충분히 크다면 그 inlier를 이용해서 더 정밀한 Transformation을 구한다.
-
1~3 과정을 반복하며 가장 큰 inlier를 찾도록 개수를 추적한다.

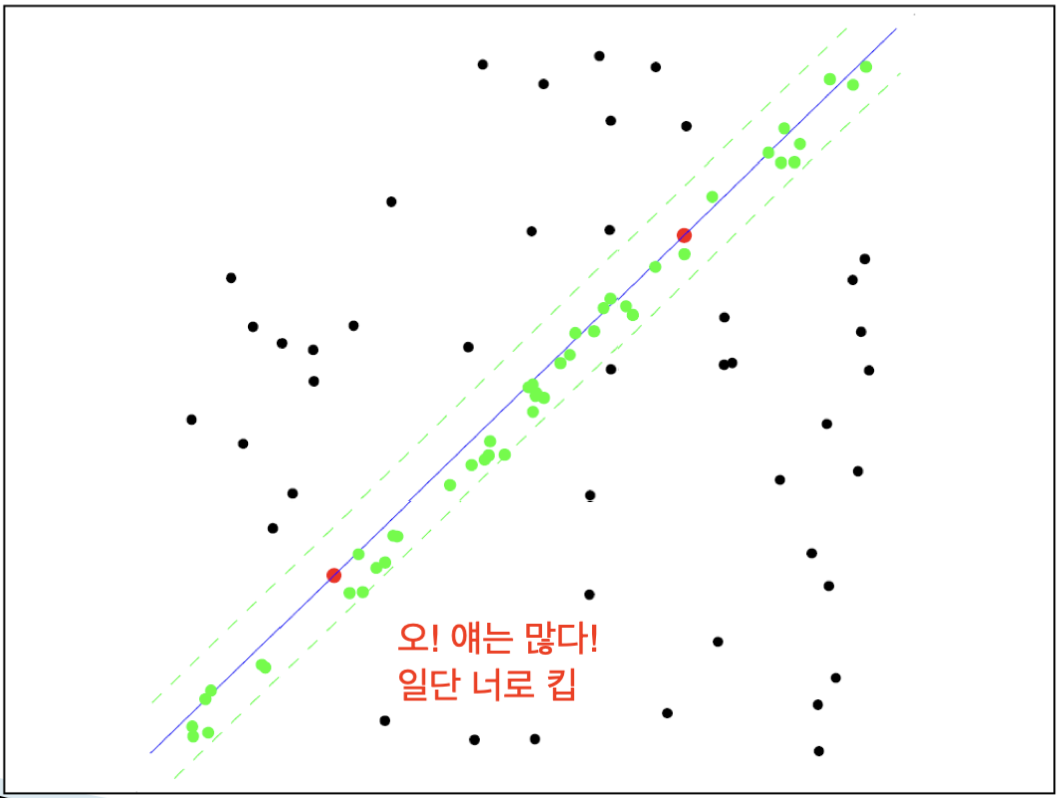
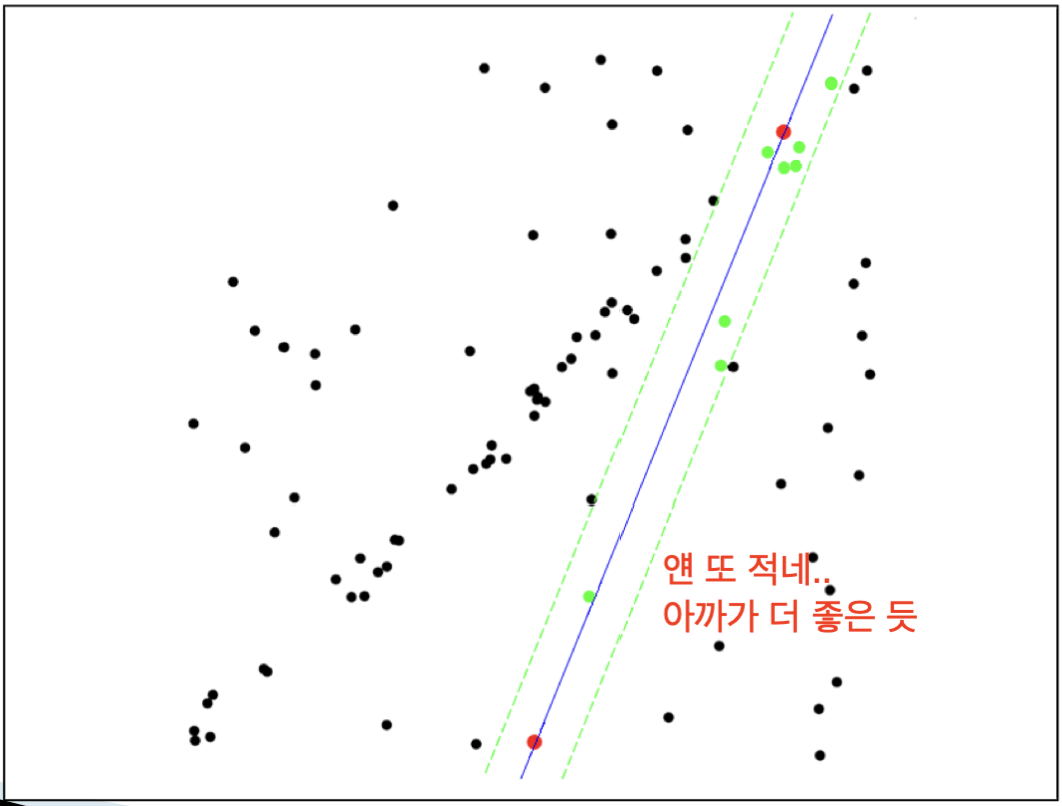
단, 이런 알고리즘의 특성 덕분에 대부분의 데이터가 inlier로 존재하고, 일부 데이터만이 outlier로 존재하는 경우에만 잘 동작합니다.
calculate trial counts
그렇다면 유효한 fitting을 하기위해 얼마나 많은 비교 연산(시도)을 해야할까?
p를 inlier의 비율이라 하고, s를 시도횟수라고 하자.
이 때, 특징점 k개를 모두 inlier에서만 선택할 확률은 이다.
즉, 특징점에 outlier가 포함되는 확률은 이다.
이 때, fitting을 하기위해 s번 시도를 하는데, s번 동안 모두 outlier가 포함되어 피팅이 되는 확률은 이며, 이 확률은 RANSAC이 실패하여 피팅에 실패할 확률을 의미한다.
따라서 P가 피팅에 성공할 확률이라 한다면 1-P는 피팅에 실패할 확률이란 뜻이고, 아래와 같은 관계식이 도출된다.
예로 들어 90%가 inlier이고(p=0.9), 특징점 샘플의 수는 50개(k=50) 이며, 99.9% 확률로 피팅에 성공(P=0.999)해야 한다고 했을 때,
즉, 약 1300번 정도의 시도를 해야 99.9% 확률로 피팅에 성공할 수 있다는 뜻이다.