웅덩이

Kernel

Filtering과 Convolution에 적용할 데이터를 Kernel 이라고 부른다.
즉, 원본 영상에 어떤 커널을 Filtering 혹은 Convolution 하느냐에 따라 다른 출력물이 나오는 것이다.

커널에 적용방식은 뒤에 Filtering과 Convolution에서 다룰 예정이니 참고만 하고 나중에 다시오자.

Moving Average (Smoothing)

가로, 세로가 N인 배열의 원소가 모두 $1/N^2$ 로 채워진 커널이다.
이 커널을 적용하면 이미지가 뿌옇게 변하게 된다.

Laplacian

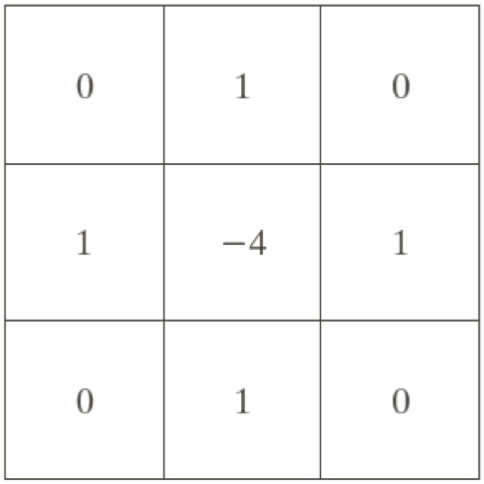
3 $\times$ 3 배열에 중심이 -4, 상하좌우가 1, 나머지가 0으로 채워진 커널이다.
이 커널을 적용하면 이미지 주변부가 강조되고, 중심부는 약화된다.

Laplacian을 적용한 필터를 원본 이미지에서 빼는 방식으로 Sharping Filter를 구현할 수 있다.

Shift

중심으로부터 n만큼 떨어진 거리에 1, 나머지는 0으로 채우면 Filtering의 경우 해당 방향의 반대 방향으로 영상이 이동한다.
예로 들어 3 $\times$ 3 배열 중 가운데 왼쪽만 1, 나머지는 0인 커널로 영상을 Filtering시 영상은 오른쪽으로 1픽셀 Shift된다.

Filtering

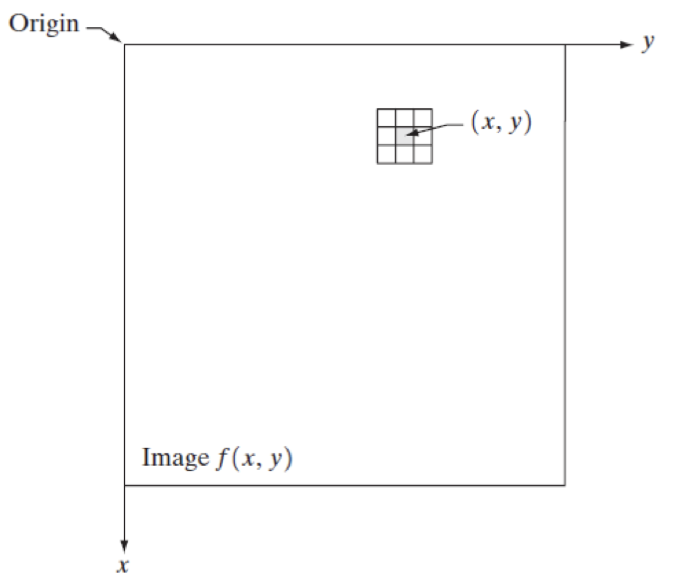
231017-225146

영상의 주변부의 값을 이용해 변형시키는 과정을 필터링이라고 한다.
필터링 과정은 LTI System에서 이루어진다.

이 필터링은 크게 Correlation Filtering (just Filtering)과 Convolution Filtering (just Convolution)으로 나뉘게 되는데,
두 방식의 차이를 비교해보며 위에서 소개한 두 커널을 적용하면 이미지가 어떤식으로 바뀌는지 알아보자.

Filtering (Correlation)

g(m,n) = f(m,n) * h(m,n) \\ = \sum_{k=m-a}^{m+a}\sum_{l=n-a}^{n+a}f[k,l]\times h[m-k,n-l]

필터링은 커널의 변형이 없이 연산된다.

위 수식을 보면 픽셀별로 주변 $a$ 만큼의 픽셀의 값을 참고하여 연산이 진행됨을 알 수 있는데, 이를 아래 그림으로 살펴보자.
이 때 사용한 커널은 위에서 언급한 Moving Average 커널이다.

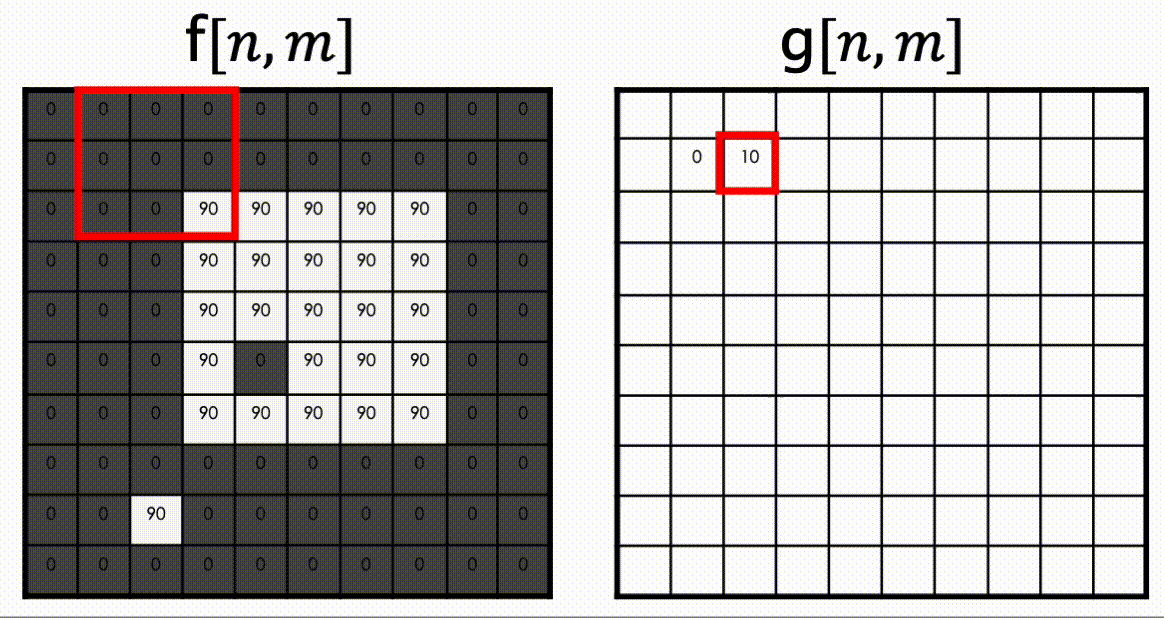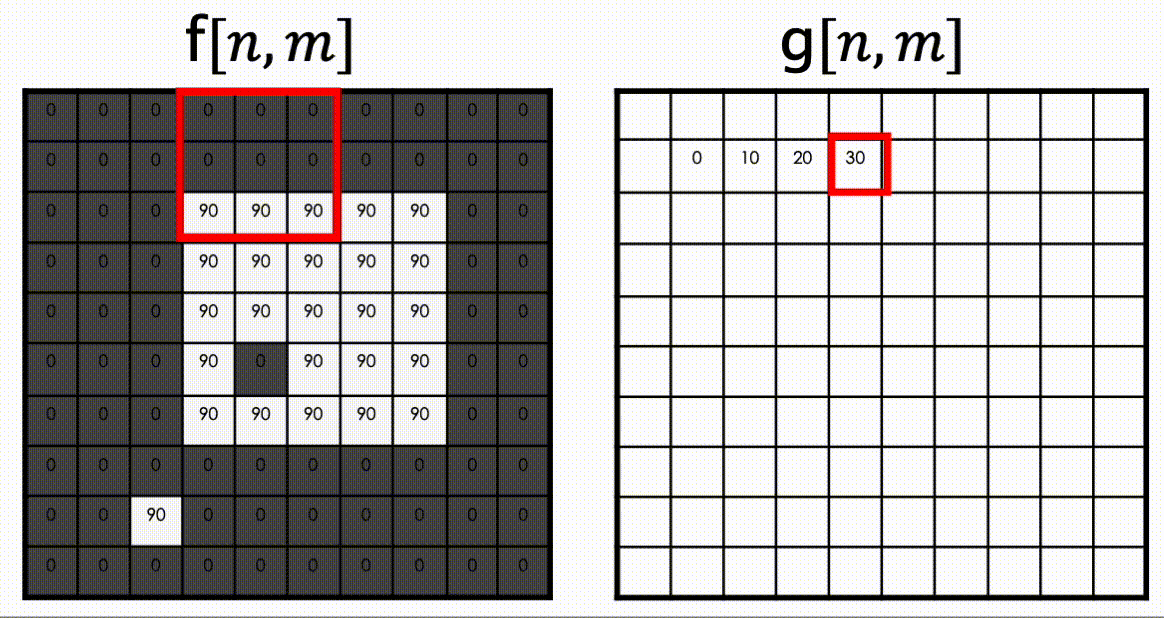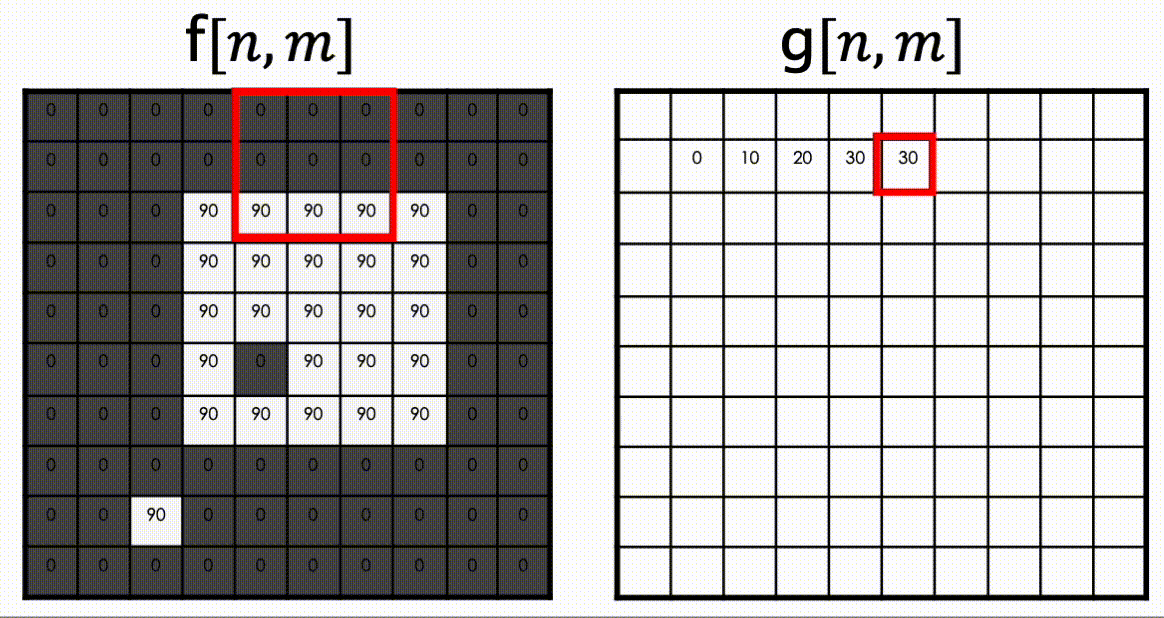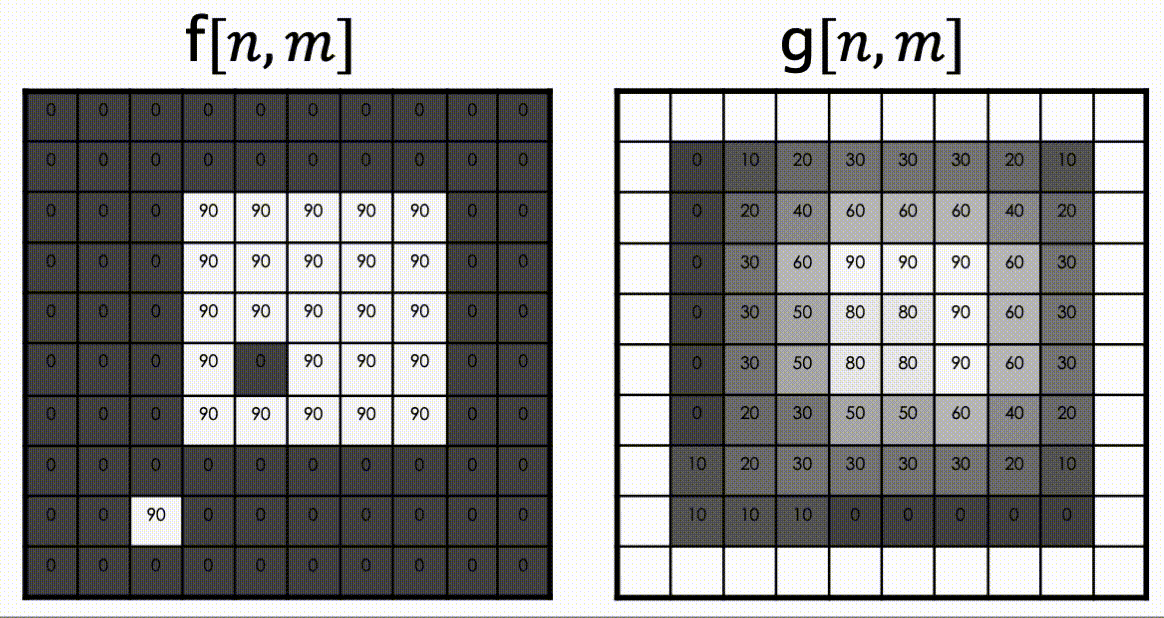
filtering_gif

위 영상은 커널사이즈가 3 $\times$ 3 ( $a=1$ )인 Moving Average Kernel을 Filtering 한 결과이다.
전반적으로 화면이 뿌옇게 변하는 영상을 얻을 수 있다.

Convolution

g(m,n) = f(m,n) * h(m,n) \\ = \sum_{k=m-a}^{m+a}\sum_{l=n-a}^{n+a}f[k,l]\times h[n-k,m-l]

자세히 보면 h의 m, n의 위치가 Filtering과 반대이다.
즉, 컨볼루전은 커널이 대각선 반전되어 연산된다.

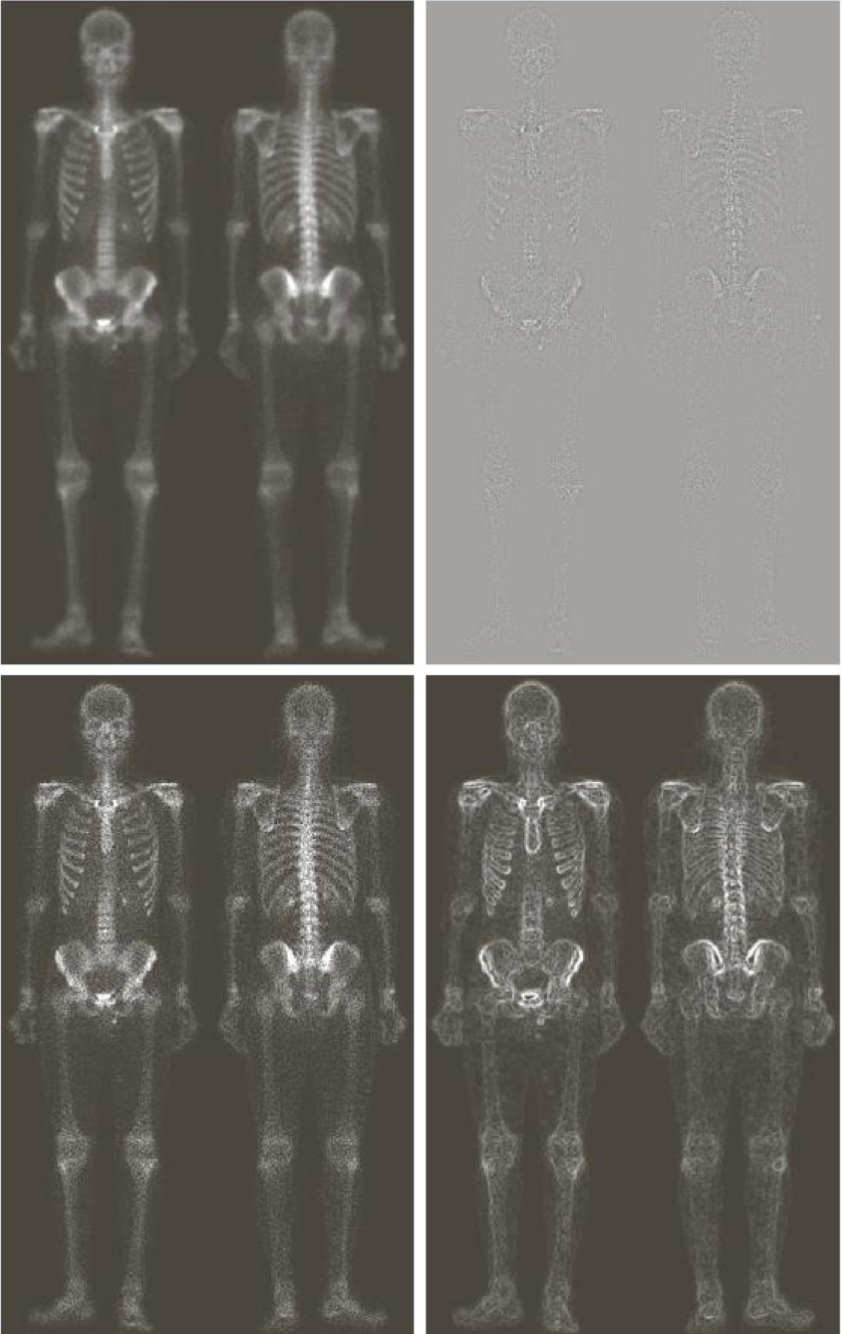
231018-204207

좌상단은 원본 영상, 우상단은 그 원본 영상에 Laplacian 커널을 Convolution한 결과이다.
좌상단 영상에서 우상단 영상을 빼면 좌하단과 같이 영상의 윤곽선이 선명해지는 Sharping Filter를 구현할 수 있다.
그런데 이게 어떻게 가능한걸까?

이걸 가능케 하기 위해선 우선 사람이 빛을 인지할 때 그 민감도를 인지하는 법을 알아야 한다.

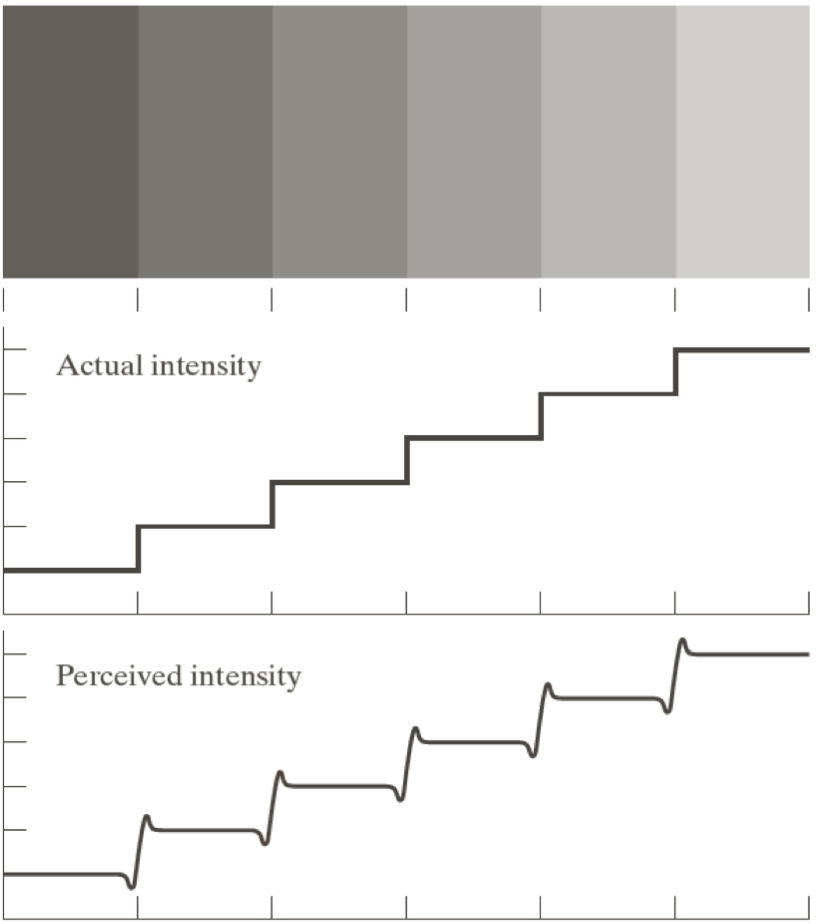
231018-204430

사람이 밝은 빛을 보다가 어두운 빛을 보면은 원색보다 더 어둡게 느끼고,
어두운 빛을 보다가 밝은 빛을 보면은 원색보다 더 밝게 느끼는 현상이 발생하는데, 이를 이용하는 것이다.

구현할 때 빛의 밝기 변화에 초점을 맞춰보자.
변화, 즉, 미분을 이용하는 것이다.

밝아진다 → 기울기가 양의 기울기 → 기울기가 증가함

그림으로 살펴보자.

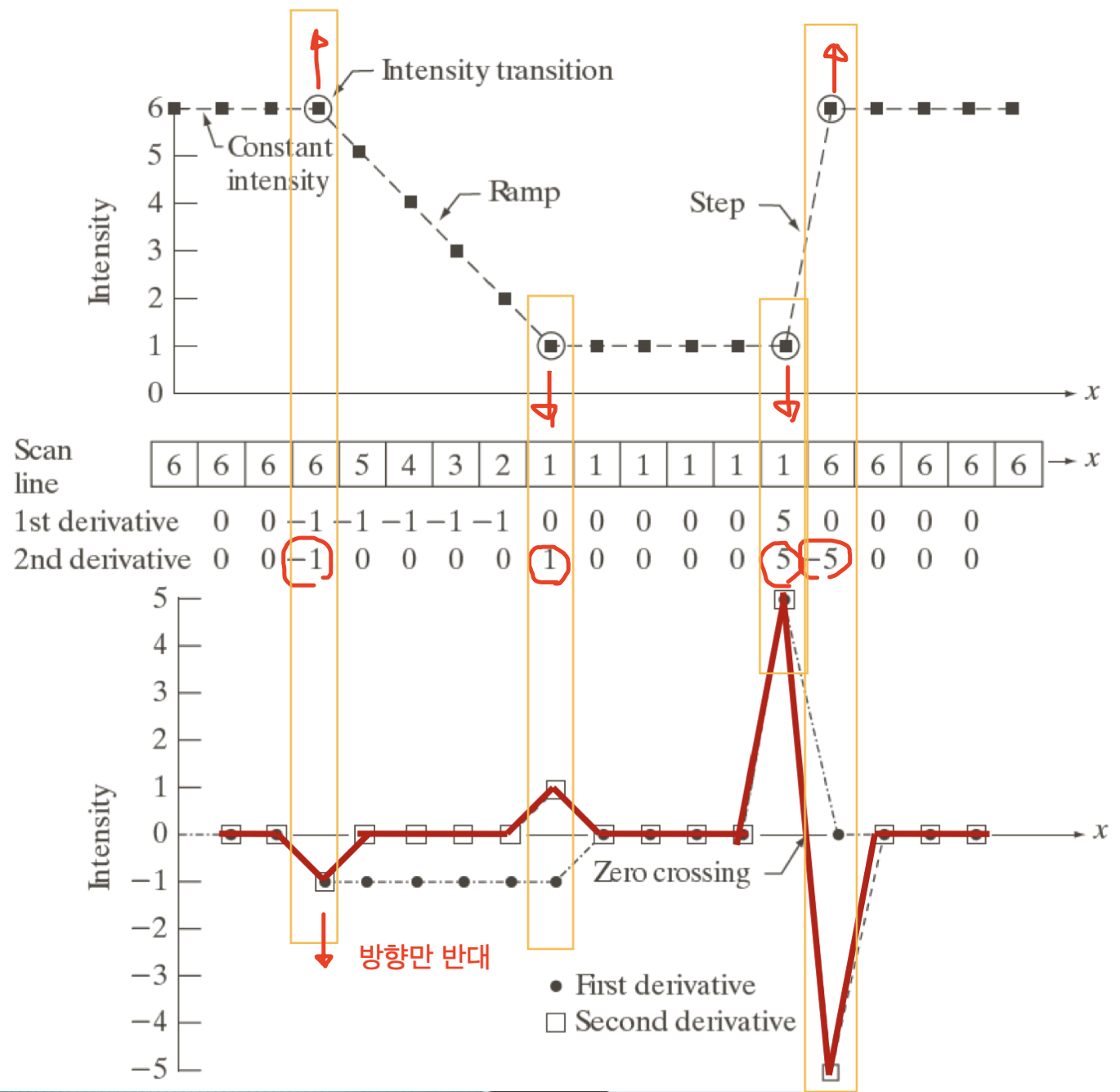
231018-204831

밝기가 감소하기 시작하는 부분의 밝기는 높여주고, 감소가 끝나는 부분의 밝기는 높여주면 선명해지는 효과가 있다.
그런데 2번 미분한 값을 보자.
우리가 원하는 변화량과 정확히 반대의 값을 갖는다.

즉, 2차 미분값을 원본 영상에서 빼주면, 우리가 원하는 Sharping Filter를 구현할 수 있다.

그런데 영상처리에서 미분계산이 너무 코스트가 크지 않을까 걱정이 된다.

f'(x) = \frac{df}{dx} = \frac{f(x + \Delta x) - f(x)}{x + \Delta x - x}

하지만, 실제로 그렇지 않다.
디지털에서 영상 처리를 할 때는 Quantization를 했기 때문에 $\Delta x$ 의 매우 작은 값은 1이 된다.
따라서 다음과 같은 식으로 정리된다.

\frac{df}{dx} = f(x + 1) - f(x) \\ {} \\ \frac{d^2f}{dx^2} = f(x + 1) - 2f(x) + f(x - 1)

이 값은 사실 각각 h[0, -1, 1] / h[1, -2, 1]의 컨볼루전과 같다.
따라서 1차원 영상의 경우에는 영상에 h[1, -2, 1] 커널을 컨볼루전 하면 된다.

2차원은 위 방식을 편미분을 사용하여 비슷한 방식으로 진행하면 된다.
x에 대한 편미분 + y에 대한 편미분 값을 더하면 다음과 같은 3 $\times$ 3 배열이 나오는데, 이 배열을 컨볼루전하면 원하는 Laplacian Filter를 구현할 수 있다.

231018-210553

Boundary (Edge)

Filtering 부분에서 gif영상으로 봤을 때 가장자리는 데이터를 채워주지 못했다.
그 이유는 커널 중심을 가장자리 영역으로 잡았을 때, 영상 외부의 값을 참조해야 값을 계산해야 하기 때문이다.

이런 부분에 대한 해결책으로 간단하게 3가지만 알아보자.

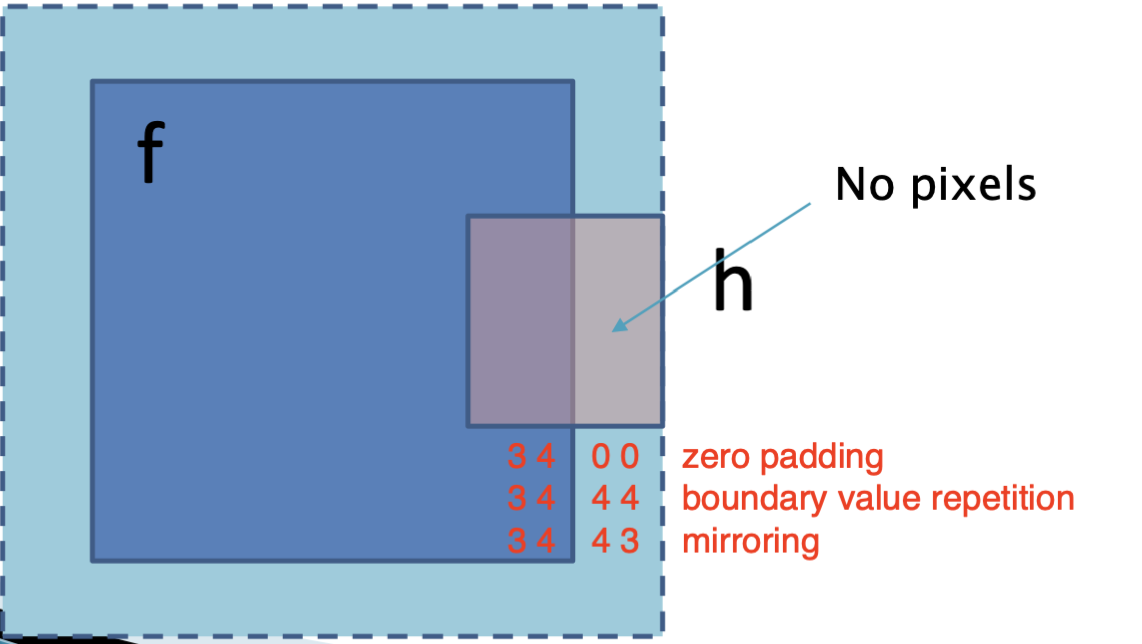
231018-210916

zero padding 방식은 없는 영상 영역을 0으로 채우고 하는 간단한 기법이다.

boundary value repetition은 최외각 픽셀의 데이터를 반복하여 채우는 간단한 기법이다.

mirroring은 마치 거울이 있는것 처럼 픽셀값을 반사하여 채우는 기법이다.