웅덩이

LTI System

Linear Time Invariant System은 다음과 같은 성질을 갖는다.

Linear
선형성을 유지한다.

선형성

H[a_if_i(x,y) + a_jf_j(x,y)] \\ = a_iH[f_i(x,y)] + a_jH[f_j(x,y)] \\ = a_ig_i(x,y) + a_jg_j(x,y)

Time Invariant
시간에 대해 불변성을 갖는다.
즉, 시간이 변해도 delay만 있을 뿐, 동일한 input에 대해 동일한 output을 내보낸다.

System Response

신호 처리를 위해 신호를 디지털화 한 다음 변환(filter)을 가해서 다시 연속적인 신호로 변환하기 위한 과정을 살펴보자.

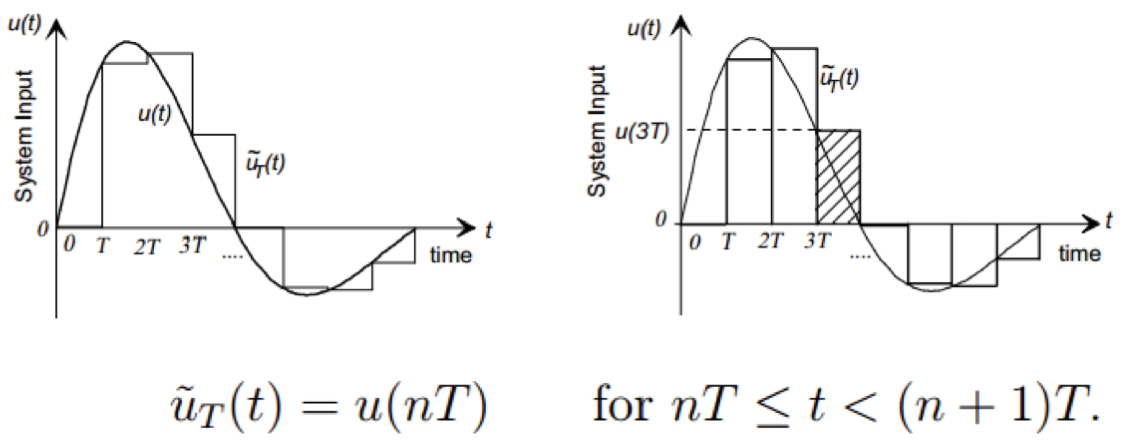
231015-222017

우선 신호를 특정 구간에서 일정한 값으로 근사한다.
그리고 특정 구간에 대해 근사된 데이터에 변환(filter)를 가한다.
(참고로 filtering에 대해선 추후에 소개할 예정. 지금은 LTI System을 이용해서 신호를 변환하는 과정만 살펴보자.)

그렇게 변환된 데이터를 다시 연속적인 신호로 변환하기 위해선 LTI System에 Pulse를 적용한 결과를 응용하면 된다.

231015-222538

넓이가 1인 Pulse를 LTI System에 통과시키면 위와 같은 그래프로 변형된다고 하자.
이 때, LTI System은 선형성을 유지하고 시간 불변성을 갖기 때문에 Pulse의 세기가 커지거나, 시간이 shift돼도,
LTI System을 통과해도 그 변화가 유지된다.

그렇기에 위에서 변환된 데이터를 특정 구간에 대해 Pulse라고 생각한다면,
그 데이터를 LTI System에 통과시키면 다음과 같이 변환될 것이다.

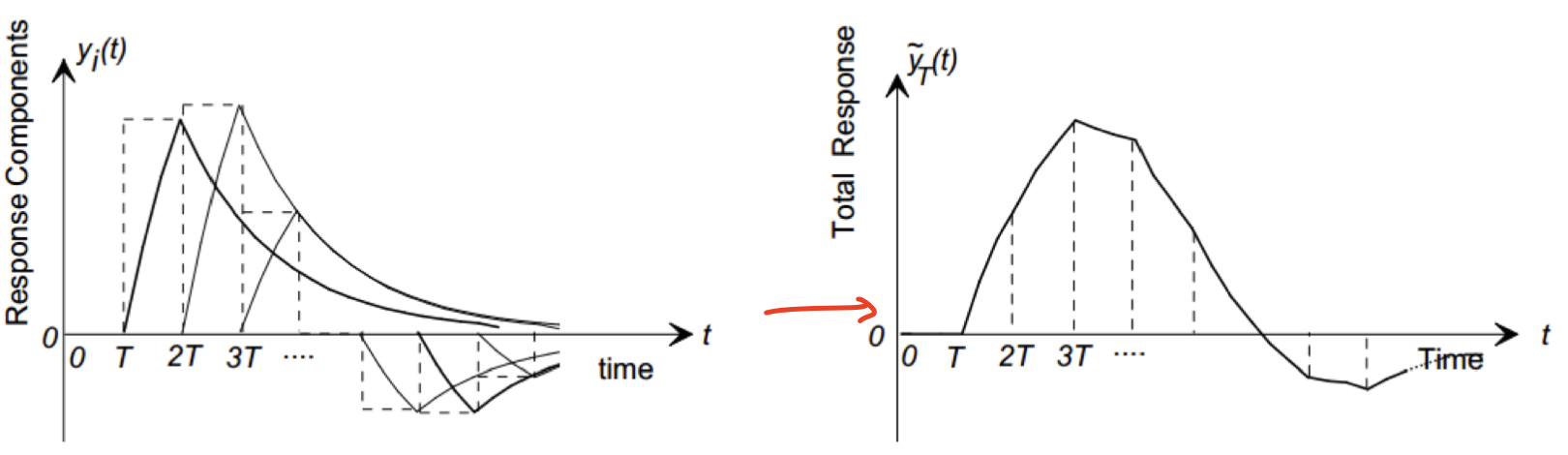
231015-222954

Convolution

위에서 언급한 Pulse에 대해 단위 시간(T)를 0에 가깝게 보내면 연속적인 신호에 대한 Pulse가 되는데, 이를 Impulse라고 한다.
이런 Impulse를 LTI System에 통과시키면 위에서 봤던 그래프 형태로 나오게 되는데, 이를 임펄스 반응 이라고 하고, $h(t)$ 라고 하자.

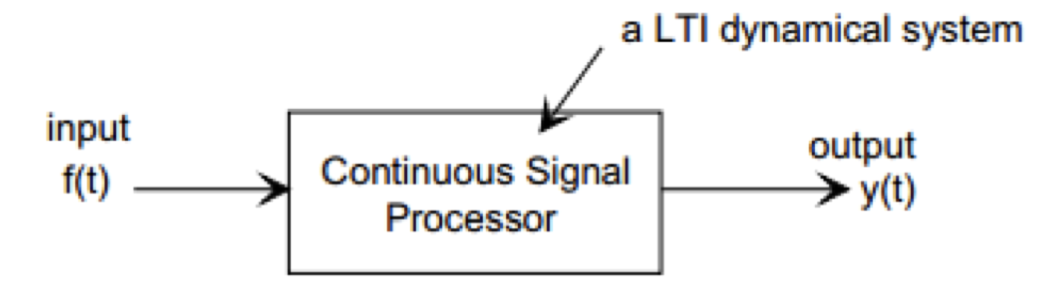
231015-223956

입력 신호 $f$ 와 출력 신호 $y$ 는 다음과 같은 관계를 갖게 된다.

y(t) = f(t) * h(t)

즉, LTI System의 출력( $y$ )은 시스텝의 임펄스 반응( $h$ )과 입력( $f$ )의 Convolution이다.

Fourier Transform

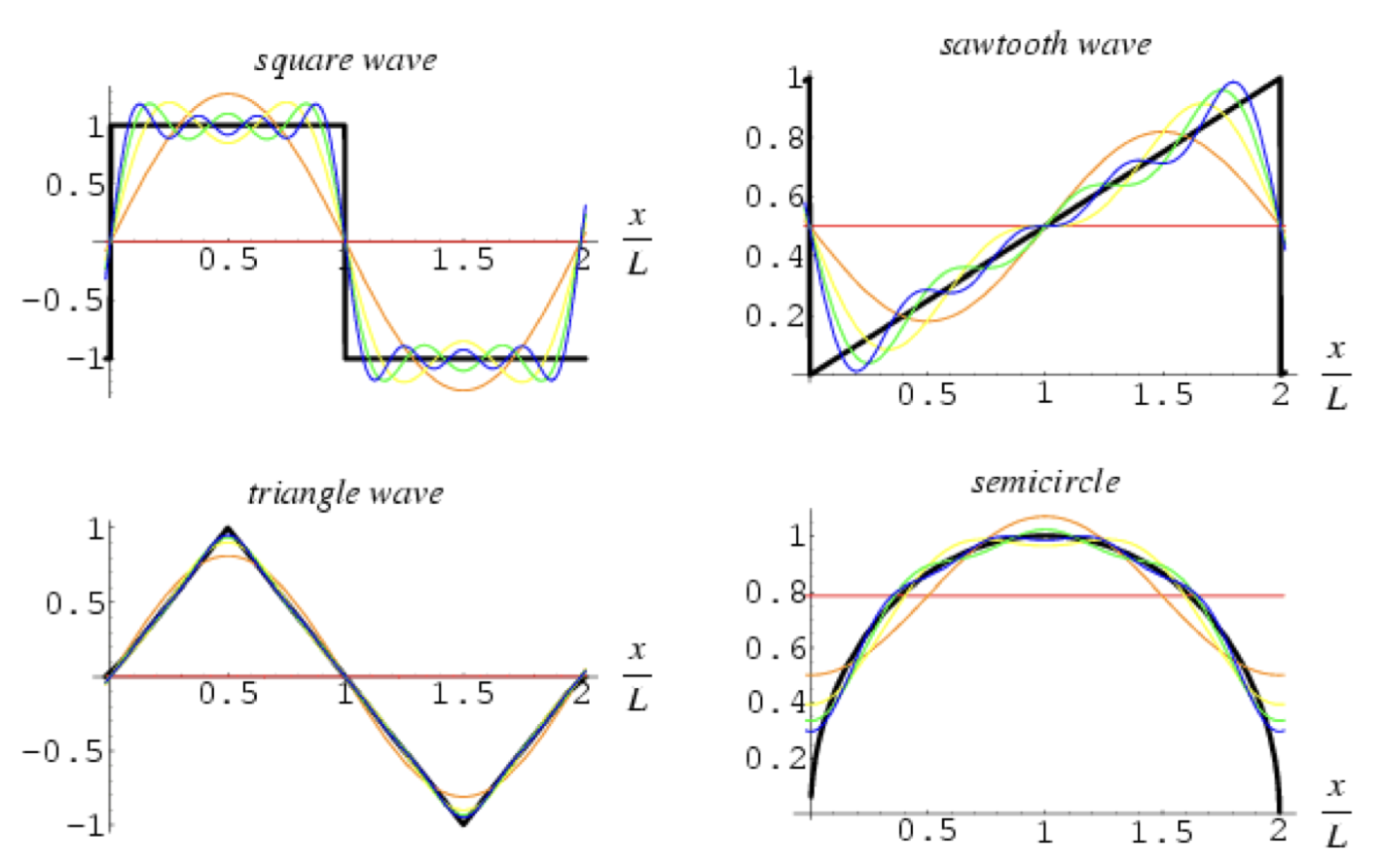
231015-224927

푸리에 변환의 기본적인 아이디어는 주기적인 어떠한 함수는 모두 sin파 또는 cos파의 합으로 표현(근사)될 수 있다에서 출발한다.

푸리에 변환을 거치면 시간에 대한 함수가 주파수에 대한 함수로 변환되는데,
시간 축이 주파수 축으로 변환된다는 뜻이다.
단적인 예로, 주기가 $2\pi$ 이고, 크기가 1인 sin함수는 크기가 1이고, $u=1 (2\pi)$ 인 Impulse 형태로 그려진다.

푸리에 변환

F(u) = \int_{-\infty}^{\infty} f(x)e^{-i2\pi ux}dx

역 푸리에 변환

f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(u)e^{iux}dx

그런데 왜 푸리에 변환을 알아야 할까?
바로 푸리에 변환을 사용하면 Convolution 연산이 매우 간단한 형태로 변환되기 때문이다.

G(u) = \int_{-\infty}^{\infty}g(x)e^{-i2\pi ux}dx \\ = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(\tau)h(x-\tau)e^{-i2\pi ux}dx \\ = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}[f(\tau)e^{-i2\pi u\tau}d\tau][h(x-\tau)e^{-i2\pi u(x-\tau)}dx] \\ = \int_{-\infty}^{\infty}[f(\tau)e^{-i2\pi u\tau}d\tau]\int_{-\infty}^{\infty}[h(x')e^{-i2\pi ux'}dx'] \\ = F(u)H(u)

즉, 기존 도메인( $x$ )에서의 Convolution 연산이 푸리에 변환된 주파수 도메인( $u$ )에서는 단순 곱셈으로 표현된다.

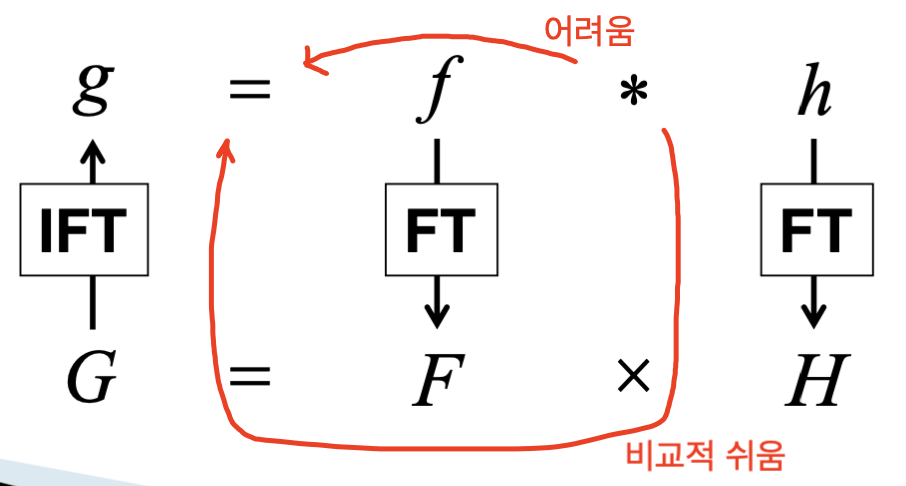
231015-230238

따라서 Convolution 연산을 간단하게 하기 위해서는 일단 푸리에 변환 후 곱연산을 수행해서 다시 역 푸리에 변환을 거치는 과정을 수행하는게 좋다.

Sampling

이전 포스트에서 Sampling이 적으면 Aliasing이 발생한다고 했었는데, 그 이유을 알아보자.

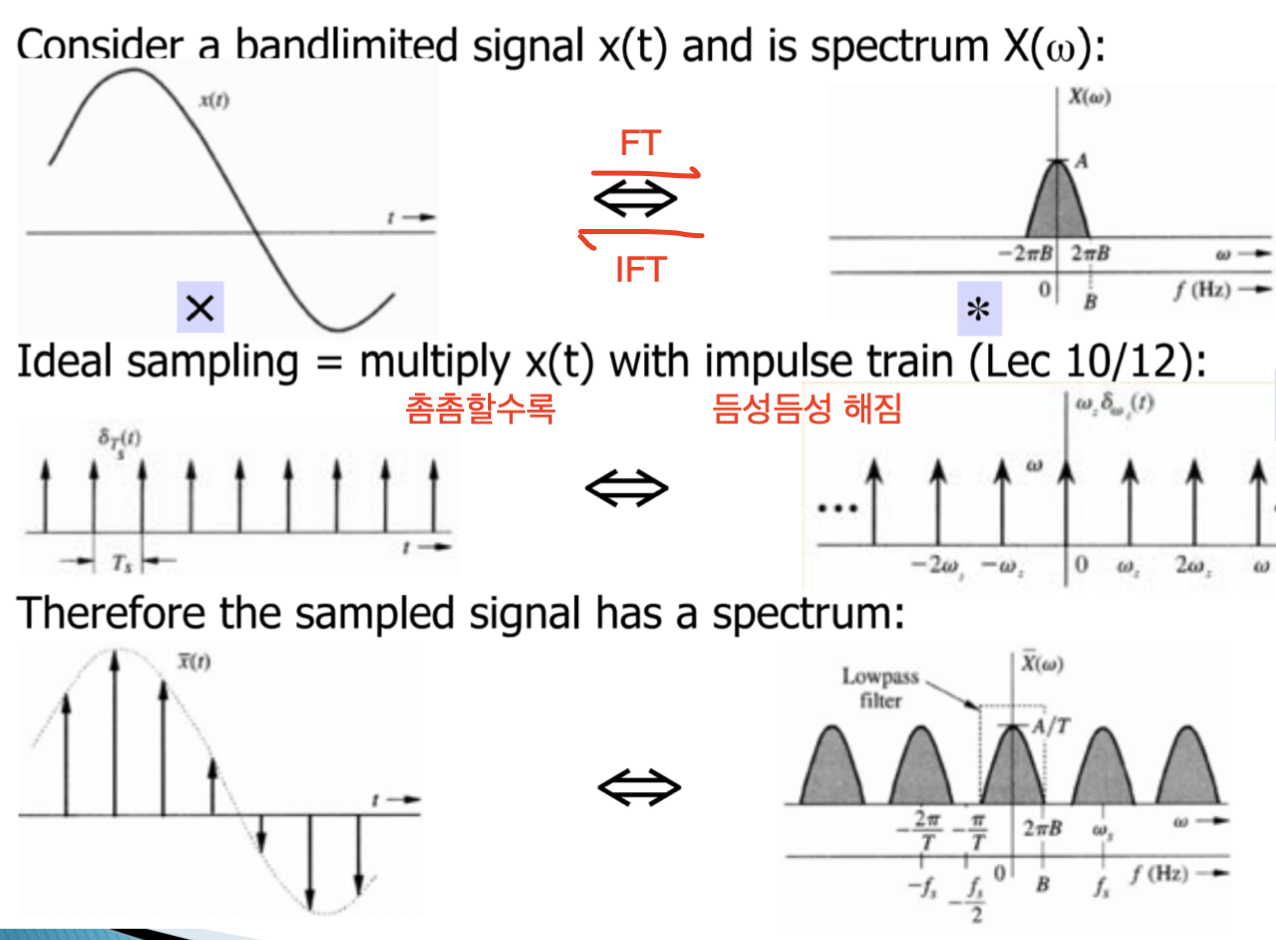
231015-230835

왼쪽은 시간 도메인 기준으로 입력 신호에 적절하게 샘플링된 Impulse를 Convolution하면 좌하단처럼 샘플링이 이루어진다.
오른쪽은 왼쪽을 푸리에 변환한 결과로 Convolution 대신 곱연산한 결과이다.

~~(본인도 이해는 안되지만)~~ 여기서 중요한 것은 샘플링이 촘촘할 수록
푸리에 변환된 스펙트럼이 듬성듬성 해진다는 점이다.

만약, 샘플링이 적은수가 되었다면 우하단의 입력 신호의 스펙트럼 봉우리(?)가 오버랩될 것이다.
오버랩 되는 경우 원본을 복구할 수 없기에 Aliasing이 발생하는 것이다.