웅덩이

Sampling & Quantization

연속적인 자연계의 현상을 기록하기 위해서는 이미지를 불 연속적인 형태. 즉, 디지털로 변환해야 한다.

예로 들어 이미지의 좌표가 100.32라면? 반올림을 하던지 적당히 100과 같은 불 연속적인 값으로 치환해야 하며,
에너지레벨 역시 이와 같은 방식으로 디지털화 해야한다.

이렇게 자연계의 연속적인(무한한) 값을 디지털화 하기 위해 유한하게 자르는 과정을 Sampling이라 하고,
무한 소수의 데이터를 양자화시켜 비트에 저장할 수 있게 자르는 과정을 Quantization라고 한다.

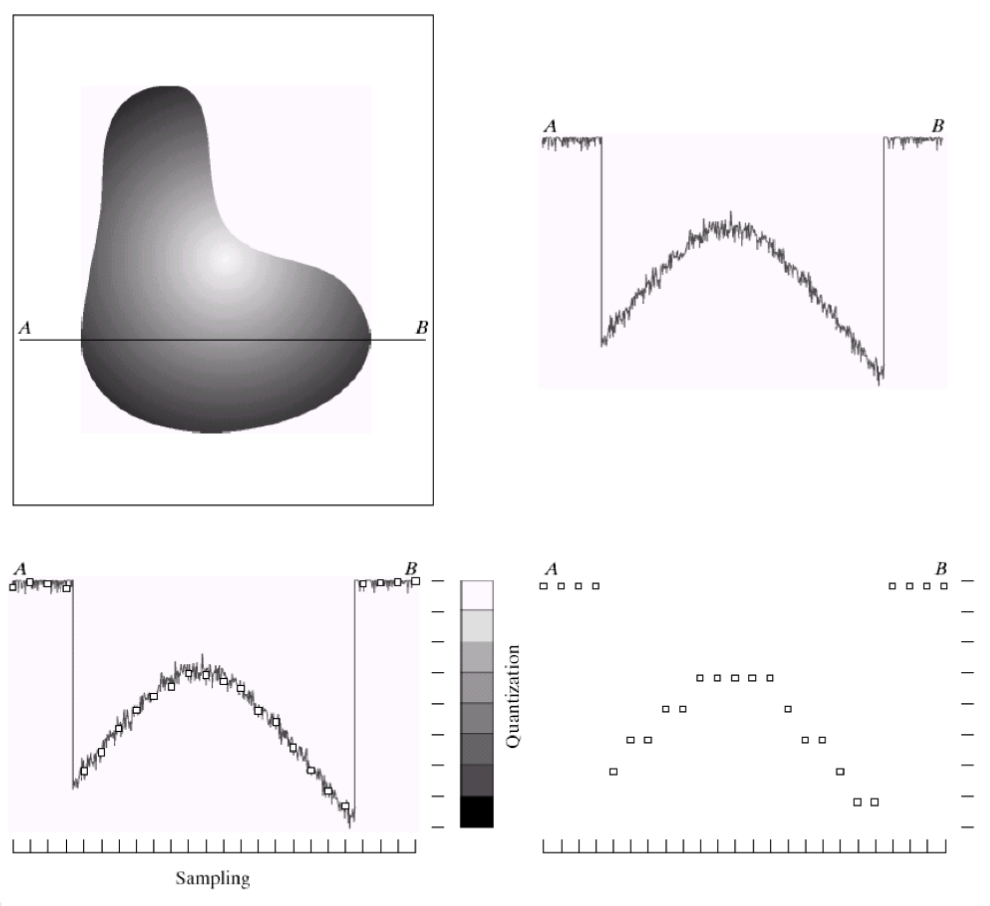
231015-201653

좌상단의 이미지 중에서 $\overline{AB}$ 를 디지털화 해본다면,
우상단의 그래프처럼 에너지레벨(빛의 밝기)이 표현될 것이다. (지글지글 거리는 것은 센서의 한계로인한 노이즈)
샘플링을 일정 구간으로 잘라 네모난 점으로 표현하면 좌하단의 이미지처럼 될 것이고,
이를 양자화하면 우하단의 이미지처렴 변화하여 디지털로 저장할 수 있게 된다.

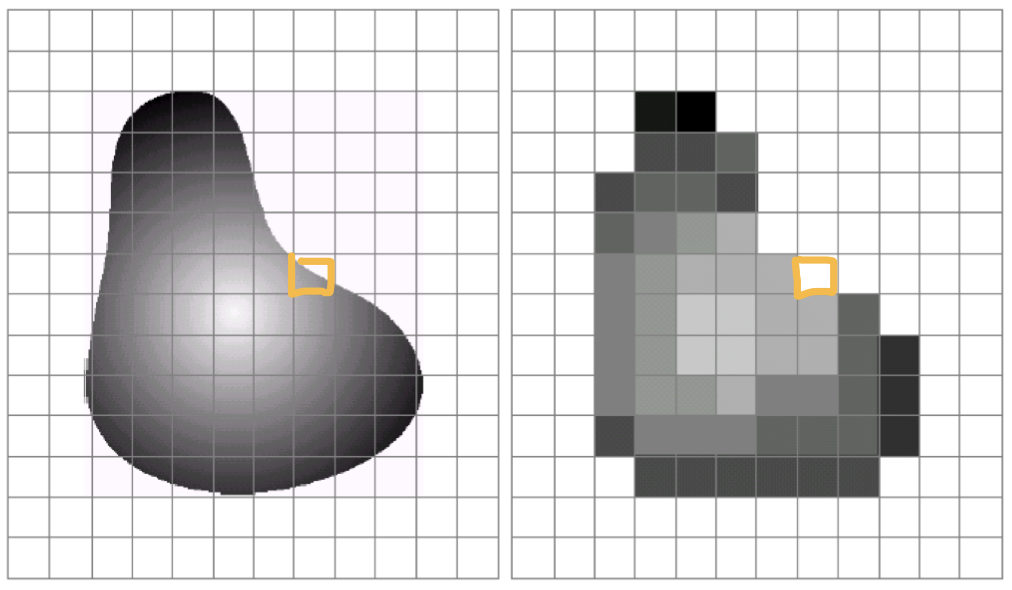
231015-202204

이런 방식으로 2차원 이미지를 디지털화 하면 위와 같은 모양이 될텐데,
연속적인 데이터를 불연속적인 데이터로 변환하면서 어쩔 수 없는 데이터의 손실이 발생할 수 있다.

픽셀의 가로축은 x축, 세로축은 y축이며,
x좌표는 늘 보던 좌표계와 마찬가지로 오른쪽으로 갈 수록 커지지만,
y좌표는 반대로 내려갈수록 커진다. (y축 반전 주의)

M행 N열(M $\times$ N)의 이미지는 다음과 같은 배열에 저장할 수 있다.

f(x,y) = \begin{bmatrix} f(0,0) & f(0,1) & ... & f(0,N-1) \\ f(1,0) & f(1,1) & ... & f(1,N-1) \\ ... & ... & ... & ... \\ f(M-1,0) & f(M-1,1) & ... & f(M-1,N-1) \\ \end{bmatrix}

Aliasing

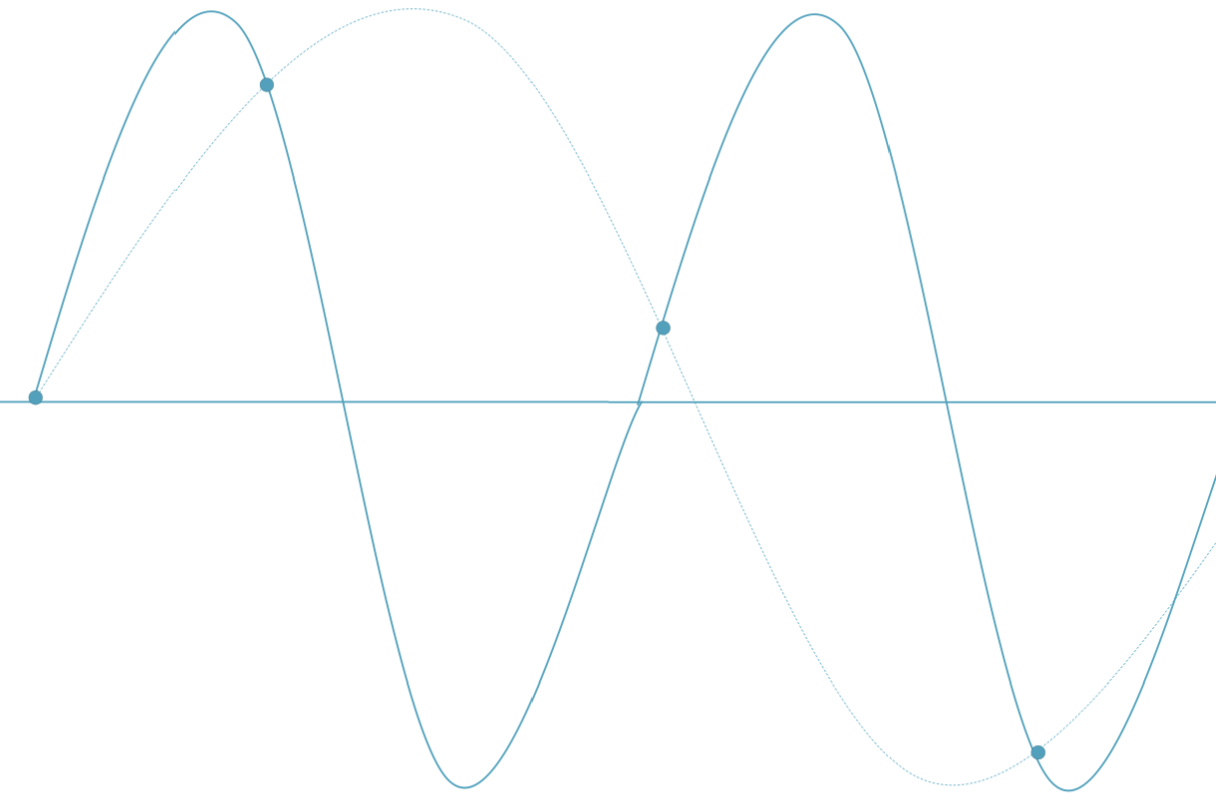
231015-205116

샘플링을 위 이미지와 같이 극단적으로 적게 할 경우, 조건이 없다면 원본 데이터를 유추할 수 없게 된다.
또는 변화량이 너무 큰 경우에도 위와 같은 Aliasing 현상이 발생할 수 있다.
예로 들어서 선풍기를 영상으로 찍으면 멈춰있는 듯한 현상이 그런 경우이다.

Quantization Level

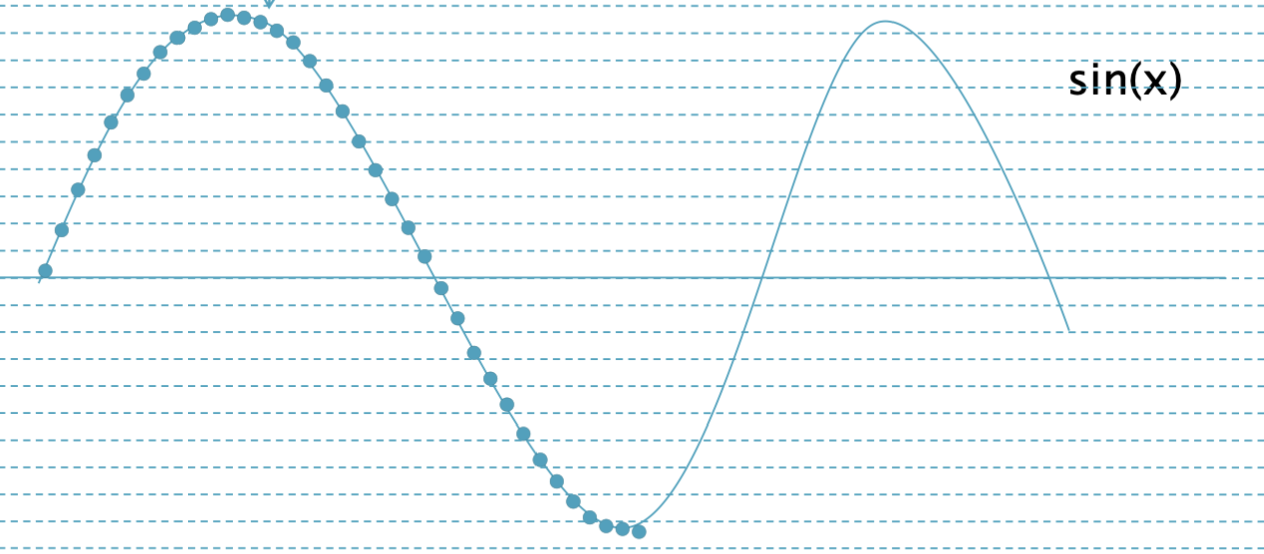
231015-204846

양자화를 얼마나 세밀하게 할지를 Quantization Level이 결정한다.
레벨이 적을수록 듬성듬성 양자화하게 되고(점선 간격이 늘어남), 이는 화질 저하로 이어진다.
하지만 용량은 절약될 것이다.

Size (Storage bits)

이렇게 저장된 영상의 크기를 구해보자.

이미지의 화질은 M $\times$ N으로 가정하고,
각 픽셀은 0~255, 즉, 8 bits의 에너지 레벨을 갖는다고 가정하자.

단색 이미지(Gray Image)의 경우 1픽셀은 8bits가 필요하기에 1byte.
이 픽셀이 M $\times$ N개 있으니 M $\times$ Nbytes.
컬러 이미지의 경우 RGB 3개의 색상 채널이 있으니 3을 곱해서 M $\times$ N $\times$ 3bytes 가 된다.

위 계산 결과는 하나의 이미지에 대한 사이즈로, 동영상의 경우에는 30프레임의 경우 추가로 30을 더 곱해줘야 할 것이다.

Saturation

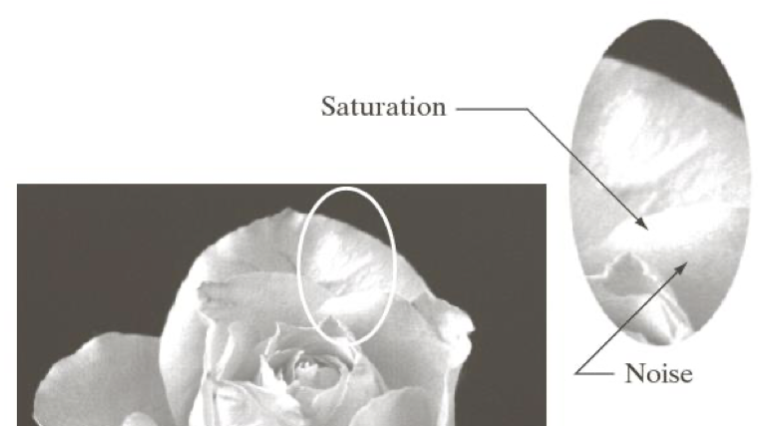
231015-203543

센서까지 차이가 있던 데이터가 샘플링 과정에서 차이가 없어지는, Saturation 현상이 발생할 수 있다.

Gray Level

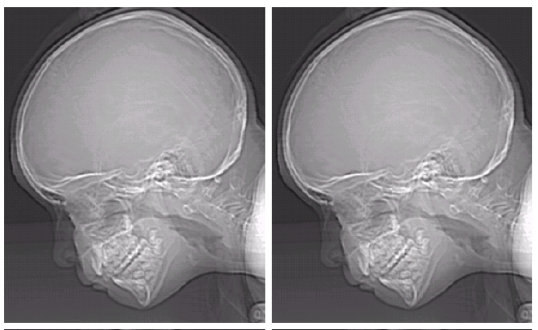
231015-203931
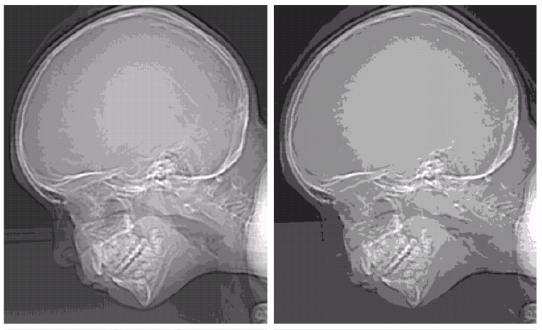
231015-203946

Gray Level이 높을 수록 에너지 레벨을 세분화해서 표현할 수 있다.
따라서 디스플레이 장치가 좋지 않아서 Gray Level이 낮을 경우 같은 이미지라도 위 사진처럼 다르게 표현될 수 있다.

Interpolation

디지털화된 이미지의 사잇값을 적절히 채워 실제 데이터를 추측하는 과정,
또는, 저화질의 영상의 픽셀값을 채워 고화질로 바꾸거나, 영상의 회전, 축소시 픽셀값을 추측하는 과정을 Interpolation 라고 한다.

Pixel math

보통 아래와 같은 행렬간의 연산 혹은 픽셀별 계산으로 처리된다.

\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{bmatrix} + \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{bmatrix} = \begin{bmatrix} a_{11} + b_{11} & a_{12} + b_{12} \\ a_{21} + b_{21} & a_{22} + b_{22} \\ \end{bmatrix}

\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} \\ \end{bmatrix}

단, 보통 픽셀값은 0~255 사이의 값을 갖기 때문에, overflow, underflow에 대해 적절하게 처리해줘야 한다.

Linear

$H[f(x,y)] = g(x,y)$ 와 같은 변환 함수 $H$ 가 있을 때,
아래의 특성을 만족하면 $H$ 가 선형이라고 한다.

H[a_if_i(x,y) + a_jf_j(x,y)] \\ = a_iH[f_i(x,y)] + a_jH[f_j(x,y)] \\ = a_ig_i(x,y) + a_jg_j(x,y)

즉 연산 순서에 상관없다면 선형이라 하며, 대부분의 이미지 처리 연산은 선형이다.

Image Rotation

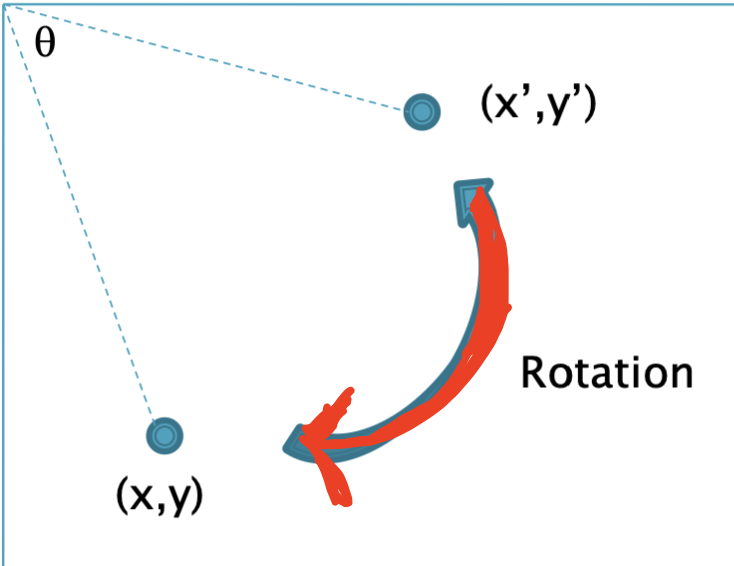
231015-212235

특정 픽셀을 $\theta$ 만큼 반 시계방향으로 회전시킬 경우 아래와 같은 연산을 가해주면 된다.

\begin{bmatrix} x' \\ y' \end{bmatrix} = R(\theta) \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

하지만, 이 경우에는 원점을 중심으로 회전되기 때문에,
영상을 중심으로 회전시켜야 하는 경우에는 다음과 같은 스탭을 거쳐야 한다.

영상을 중심으로 평행 이동 시킨다.
삼각함수를 이용해 영상을 회전시킨다.
다시 영상을 원위치로 평행 이동 시킨다.

하지만, 위 연산은 선형이기 때문에 각 픽셀별로 아래 하나의 연산으로 처리해도 상관없다.

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x - W/2\\ y - H/2 \end{bmatrix} + \begin{bmatrix} W/2\\ H/2 \end{bmatrix}

영상 변환을 하기 위해서는 변환 후(x, y)의 좌표를 연산을 통해 변환 전(x', y')의 좌표를 구하고,
그 좌표의 데이터를 가져와 Quantization하여 변환 후의 좌표에 대입하는 과정을 거쳐야 한다.

Image Interpolation

231015-214108

검은색 input 영상을 흰색 output 영상으로 upscaling하거나, 영상 회전과 같이
변환 후의 영상의 좌표가 픽셀에 정확히 들어가지 않는 경우, 검은색 픽셀값을 이용해 흰색 픽셀값을 추측해야 한다.
추측하는 방식에는 보통 아래와 같은 방법들이 있다.

Replication
이전 픽셀값의 데이터를 그대로 사용하는 방법이다.
Nearest Neighbor
본인과 가까운 픽셀의 데이터를 그대로 사용하는 방법이다.

위 두 방법의 경우 Interpolation은 가능하지만, 이미지 화질의 개선이 이루어지지는 않는다.
적당한 화질 개선을 위해서는 아래의 방법을 고려해볼 수 있다.

(Bi)linear Interpolation
근처 픽셀값을 이용해 평균 데이터를 계산하여 사용하는 방법이다.

231015-214947

q_1 = (1-a)p_1 + ap_2 \\ q_2 = (1-a)p_3 + ap_4 \\ {} \\ q = (1-b)q_1 + bq_2