Intensity Transformations
이미지 밝기 변환에 대한 내용을 다뤄봅니다.읽는데 11분 정도 걸려요.Transform Functions
입력 영상에 대해 밝기값(에너지 레벨)의 변화를 가하고 싶다면 단순히 픽셀값의 데이터에 변화를 가하면 된다.
하지만, 특정 데이터를 어떻게 변화시키는지에 따라 출력 영상이 달라지고, 거기에서 얻을 수 있는 정보도 달라진다.
그 데이터를 변화시키는 기준인 변환 함수의 종류와, 그 결과를 알아보자.
얻을 수 있는 정보가 달라진다는 표현을 사용했는데,
강조하고싶은 정보가 달라진다는 것이지 실제 정보량 자체는 변하지 않는다.
물론 임의로 특정 밝기 영역을 0으로 만든다면 정보량이 줄어들 수는 있다.
하지만 물리적인 정보량은 절대 늘어나지 않는다. (사람 눈에 보기 편하게 바꿀 뿐)
Basic
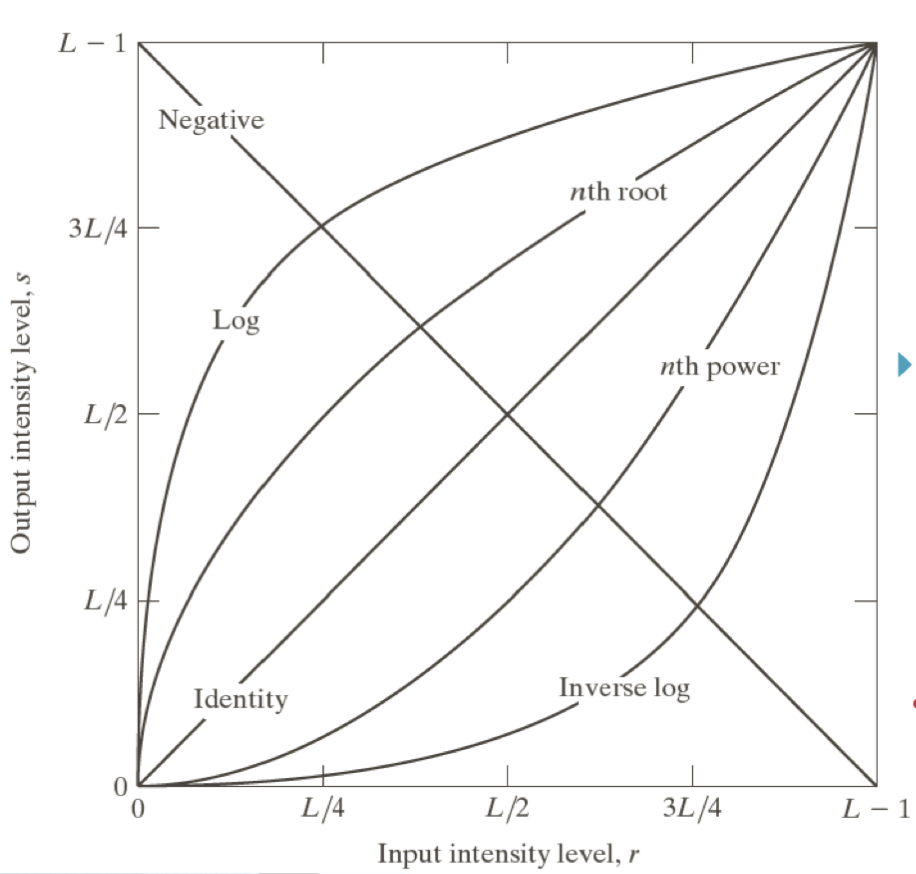
이제부터 그래프를 해석하는 능력이 중요해진다.
예로 들어 Log 함수를 변환 함수로 선택한다면 전반적으로 영상이 밝아짐을 알 수 있어야 한다.
형태의 Negative 함수를 선택한다면 영상 명암이 아래와같이 반전될 것이다.
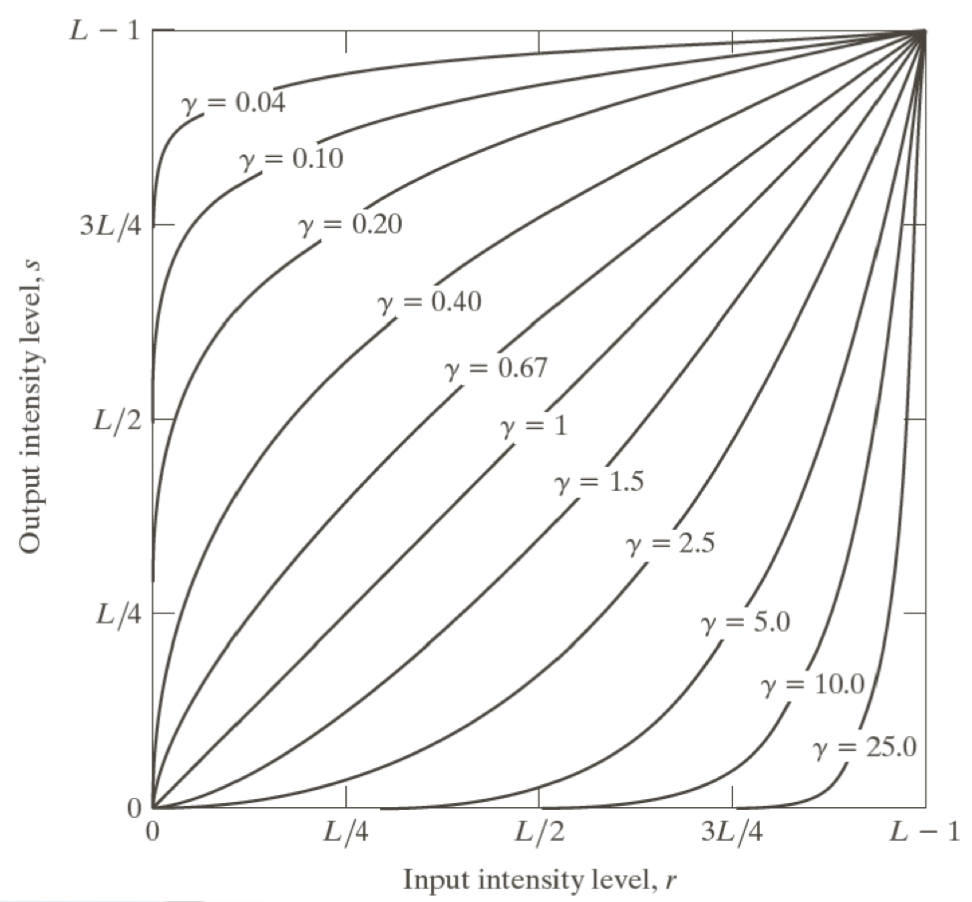
Power-Law (Gamma)
위의 기본 함수로는 세부적으로 변화시키기 힘들것이다.
하지만 아래의 함수를 이용하면 상수값()를 변화시켜 변환을 세부적으로 처리할 수 있게된다.
감마값이 커질수록 변환된 영상이 어두워지는 특징이 있다.
감마 함수는 Gamma correction에 자주 사용되곤 하는데,
이게 뭐냐면, 출력 장치의 빛의 세기를 조정해 원본 영상과 같은 영상을 디스플레이 할 수 있도록 하는 과정이다.

Piecewise-Linear
선형 커브를 여러 범위로 쪼갠 함수로
특정 범위의 값을 확장하거나, 임의의 값으로 변경할 때 사용한다.
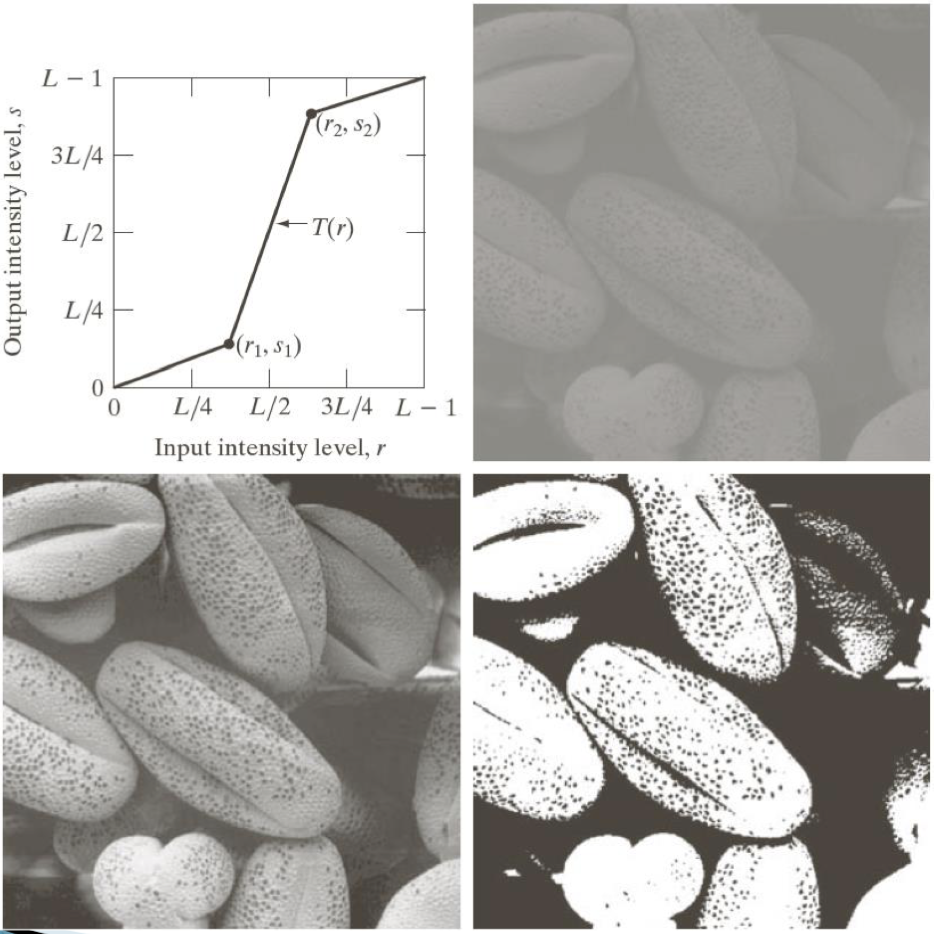
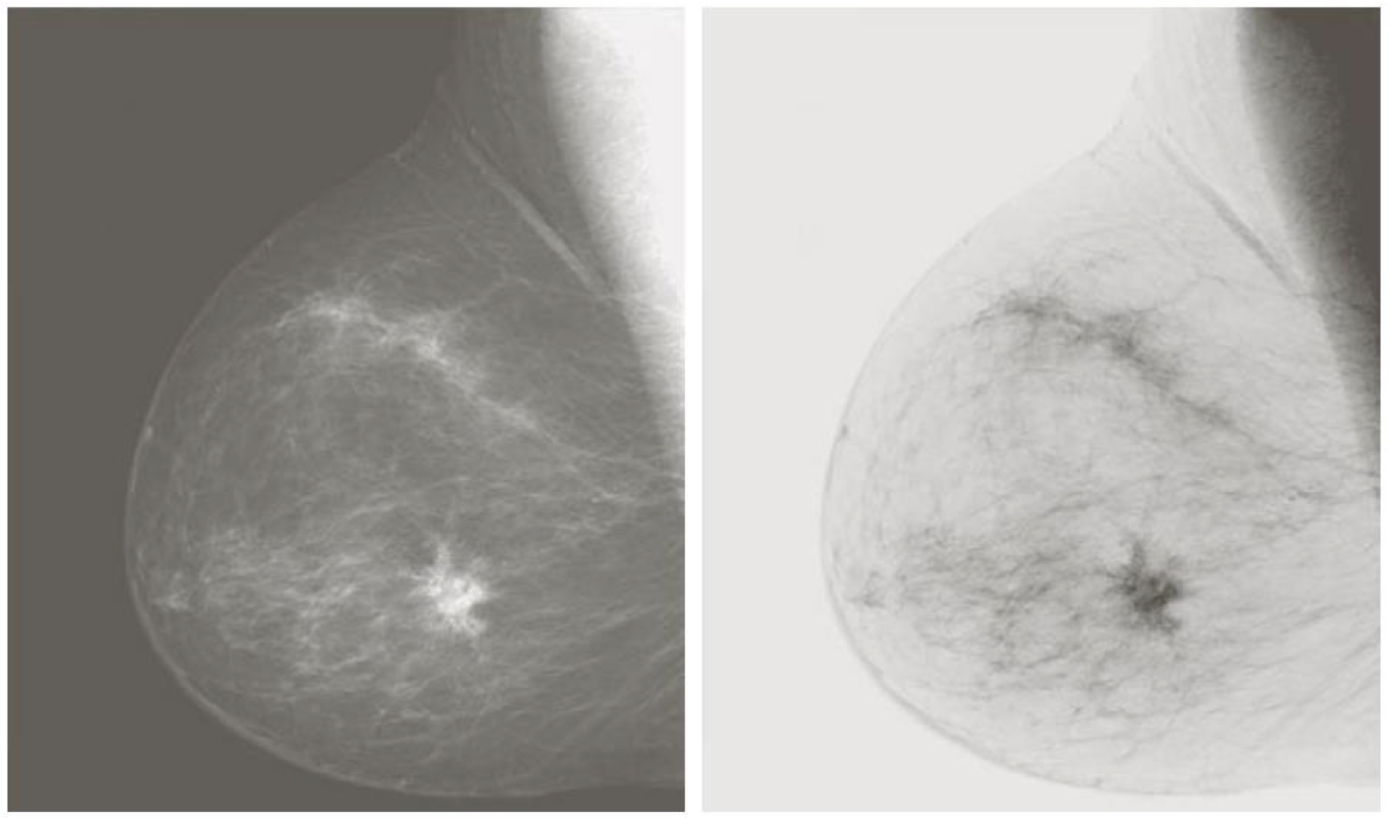
함수가 좌상단과 같이 주어질 경우 우상단의 이미지가 좌하단의 이미지처럼 변환된다.
특정 범위의 값을 확장시켜 비슷한 레벨의 빛을 분산시켜 차이를 만든 것이다.
의 기울기를 수직으로 만들면 Threshold 함수라고 불리우게 되는데,
그렇게 되면 특정 범위 이하의 빛은 검은색, 이상의 빛은 흰색으로 이분된다.
이러한 처리 기법을 Contrast Stretching 라고 부른다.
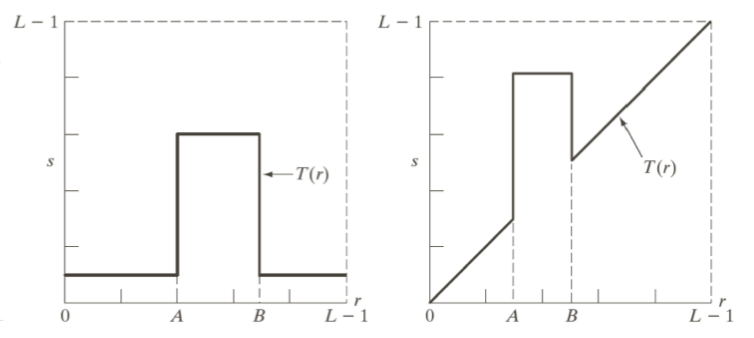
이렇게 함수가 주어진 경우에는 영상이 다음과 같이 변환된다.
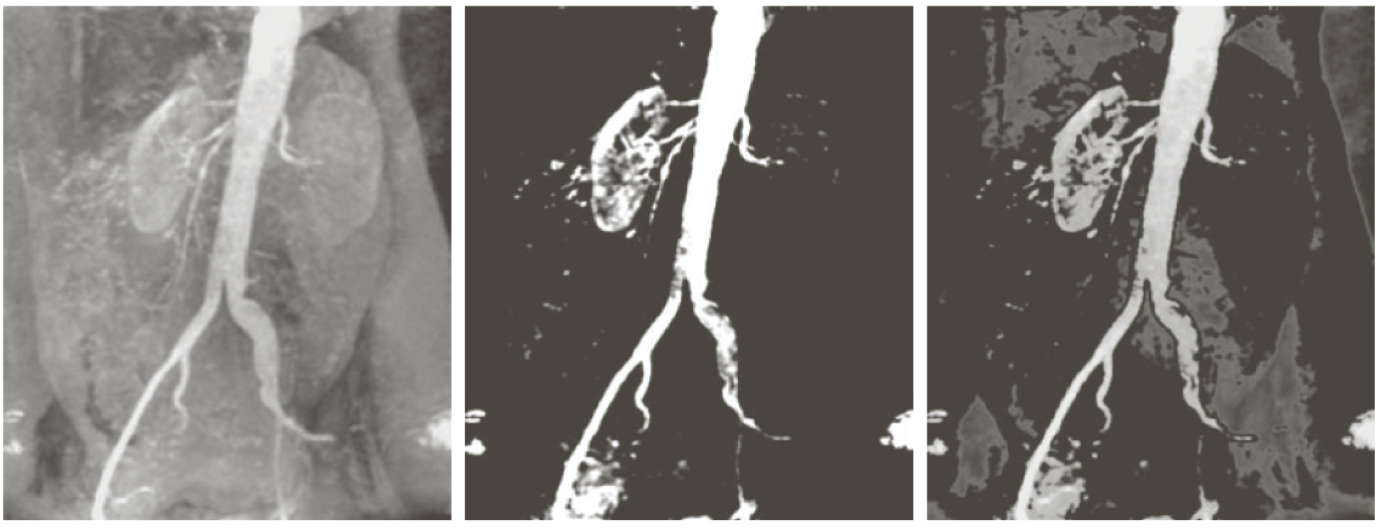
특정 부분을 제외한 나머지 영역을 죽이거나, 특정 부분만을 강조할 때 사용하는데,
이런 처리 기법을 Intensity-Level Slicing 라고 부른다.
Histogram Processing
Histogram
데이터의 분포를 한 눈에 볼 수 있는 그림 혹은 그래프
영상의 에너지 레벨 분포를 알고싶다면 다음과 같은 과정으로 구할 수 있다.
여기서 는 k번째 gray level(에너지 레벨 0~255)를 나타내고,
는 그 에너리 레벨을 갖는 픽셀의 개수를 의미한다.
코드로 구현한다면 다음과 같이 구현할 수도 있을것이다.
unsigned int Histogram[256] = {0};
for (h=0; h<H; h++) {
for (w=0; w<W; w++) {
Histogram[img[w][h]]++;
}
}
하지만 단순 픽셀 수를 세기만 한다면, 매우 큰 영상의 경우 평균적인 빛의 밝기가 어두움에도 값이 크게 나오는 문제가 발생할 수 있다.
따라서 영상 크기에 따라 자료해석의 차이를 없애도록 영상 크기로 나누어 확률로서 일반화하게 된다.
이걸 왜 하는건지 알아보기 전에 우선 서로 다른 영상별로 수집된 히스토그램을 살펴보자.
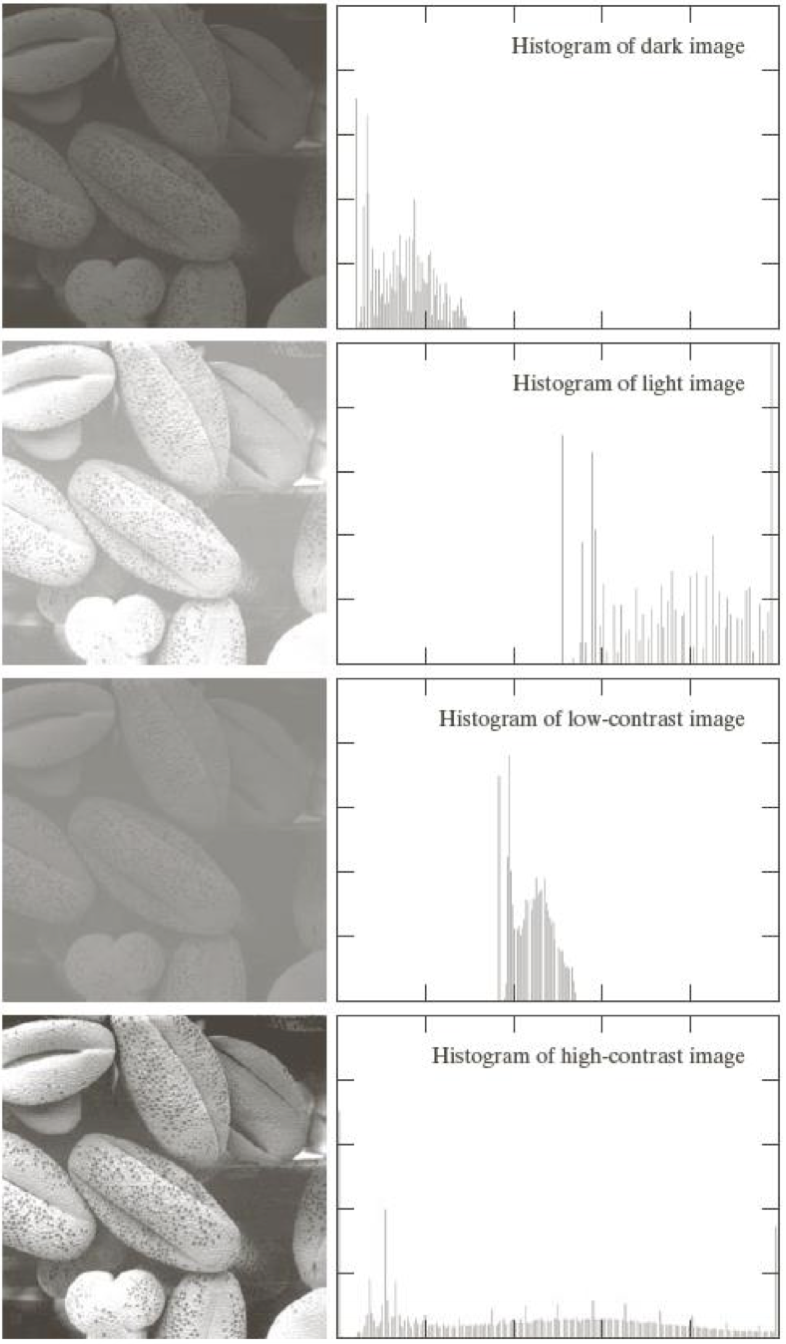
히스토그램의 분포를 살펴보면 모든 영역에 골고루 분배된 영상이 가장 보기 좋음을 알 수 있다.
그렇다면 히스토그램 분포를 분산시키는게 영상 품질 개선에 도움이 된다는 것을 알게 되었다.
Equalization
그렇다면 히스토그램 분포를 골고루 분배할 수 있을까?
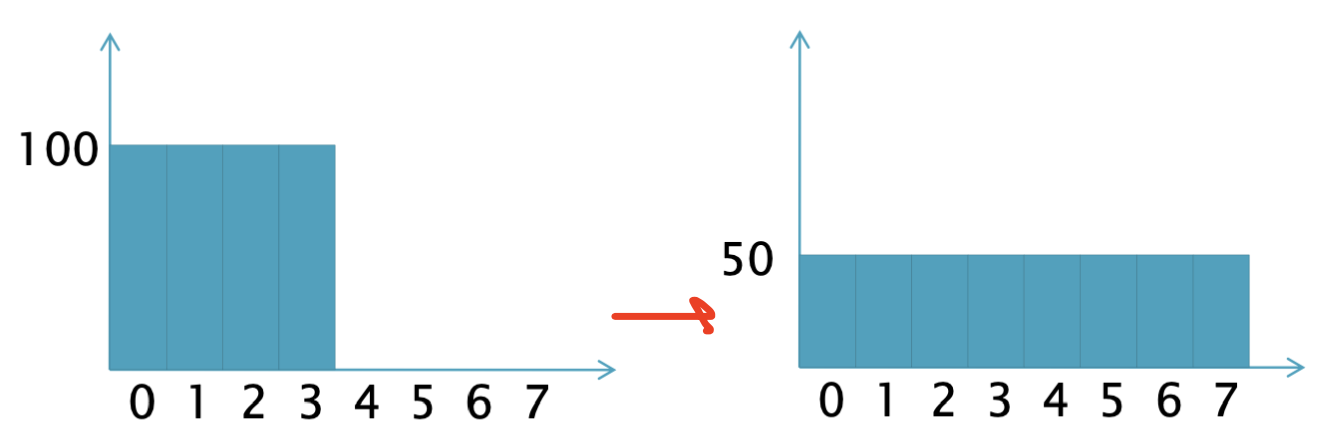
결론부터 말하면 이렇게 이상적으로 분배는 불가능하다.
0이었던 데이터를 0과 1로 적절히 분산하는 방법이 없기 때문이다.
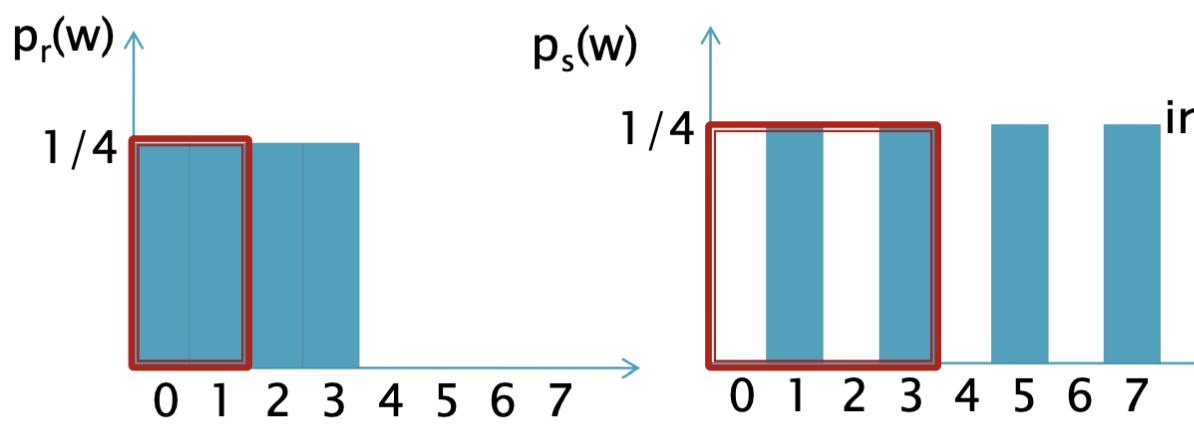
이렇게 구현하는 것이 최선일 것이다.
구현에 있어 중요한 점은 일정 범위 내의 변환 전과 변환 후의 확률 분포는 같아야 한다는 점이다.
예로 들어 변환 전의 범위 0~1은 변환 후의 범위 0~3으로 대응되는데, 각 구간의 확률의 합은 동일함을 알 수 있다.
이 사실을 식으로 일반화 하면 다음과 같아진다.
이를 연속적인 값으로 표현하기 위해 적분식으로 변환하면 다음과 같아진다.
여기서 다시 상기해보자면 은 원본 히스토그램 분포(확률 함수)이고, 는 목표로 하는 히스토그램 분포이다.
이상적인 확률 함수는 다음 그림과 같을 것이다.
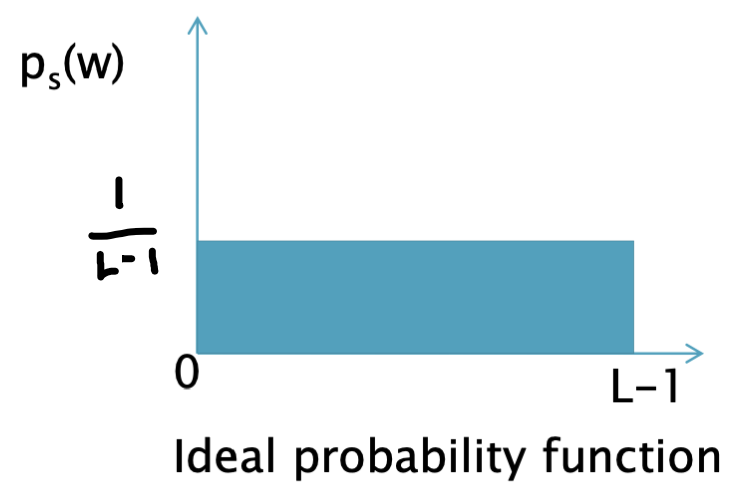
해당 함수는 로 표현 가능한데 이를 위의 적분식에 대입하면 다음과 같이 정리할 수 있다.
이제 이 공식을 이용해서 프로그래밍하기 위해 다시 불연속적인 값의 합으로 바꿔보자.
(는 일정 범위에 해당하는 x축의 값이다.)
이 때, 는 위에서 히스토그램의 확률로서 일반화 한 식을 대입하면 된다.
즉 최종 변환식은 다음과 같다.
아래 표를 기준으로 연습을 해보자.
| s_k | |||
|---|---|---|---|
| = 0 | 790 | 0.19 | = 1.33 → 1 |
| = 1 | 1023 | 0.25 | = 3.08 → 3 |
| = 2 | 850 | 0.21 | = 4.55 → 5 |
| = 3 | 656 | 0.16 | = 5.67 → 6 |
| = 4 | 329 | 0.08 | = 6.23 → 6 |
| = 5 | 245 | 0.06 | = 6.65 → 7 |
| = 6 | 122 | 0.03 | = 6.86 → 7 |
| = 7 | 81 | 0.02 | = 7.00 → 7 |
즉, 가 1이기 때문에, (0)에 존재하던 에너지 레벨을 1로 올리고,
가 3이기 때문에, (1)에 존재하던 에너지 레벨을 3로 올리는 과정을 거치면 Equalization을 달성할 수 있다.
이련 변환의 경우 히스토그램과 의 그래프는 다음과 같은 모양을 갖게 된다.
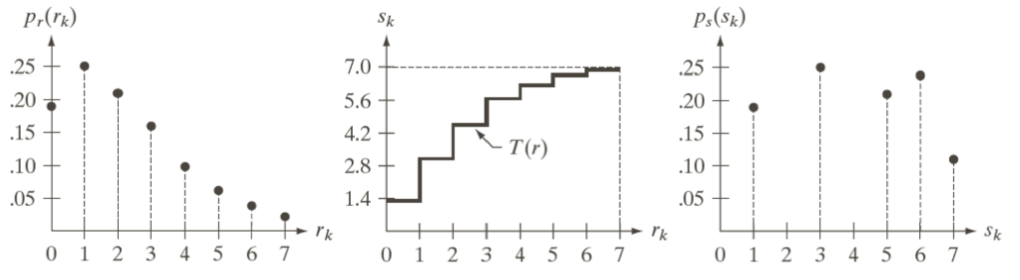
이런 경우 Equalization을 진행한 영상은 원본 영상에 비해 물리적인 정보량은 줄어들게 된다.
하지만, 사람의 눈으로 보기에는 더 보기 좋은 영상이 된다.
서로 다른 영상에 대해 Equalization을 적용한 예시와 그 함수를 살펴보자.

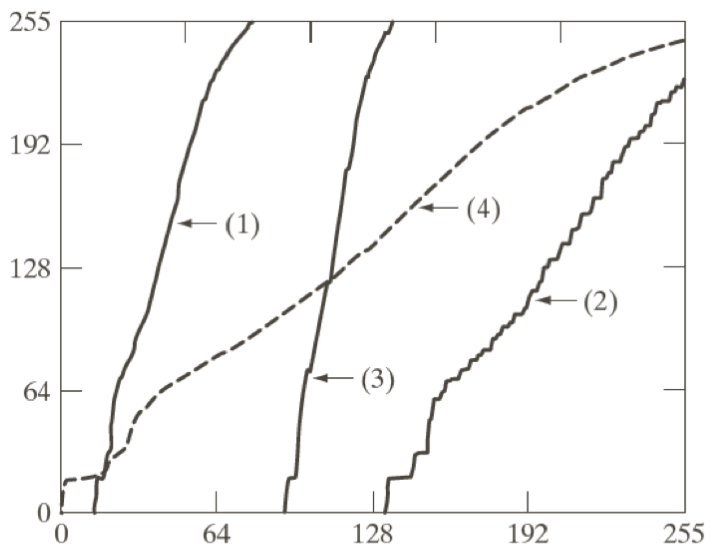
여기서 알 수 있는 점은 원본의 히스토그램 분포가 빽빽하게 모여있을 수록 변환된 영상의 히스토그램 분포에 빈공간이 많이 생긴다는 것이다. (정보량의 손실이 많아진다)
Specification
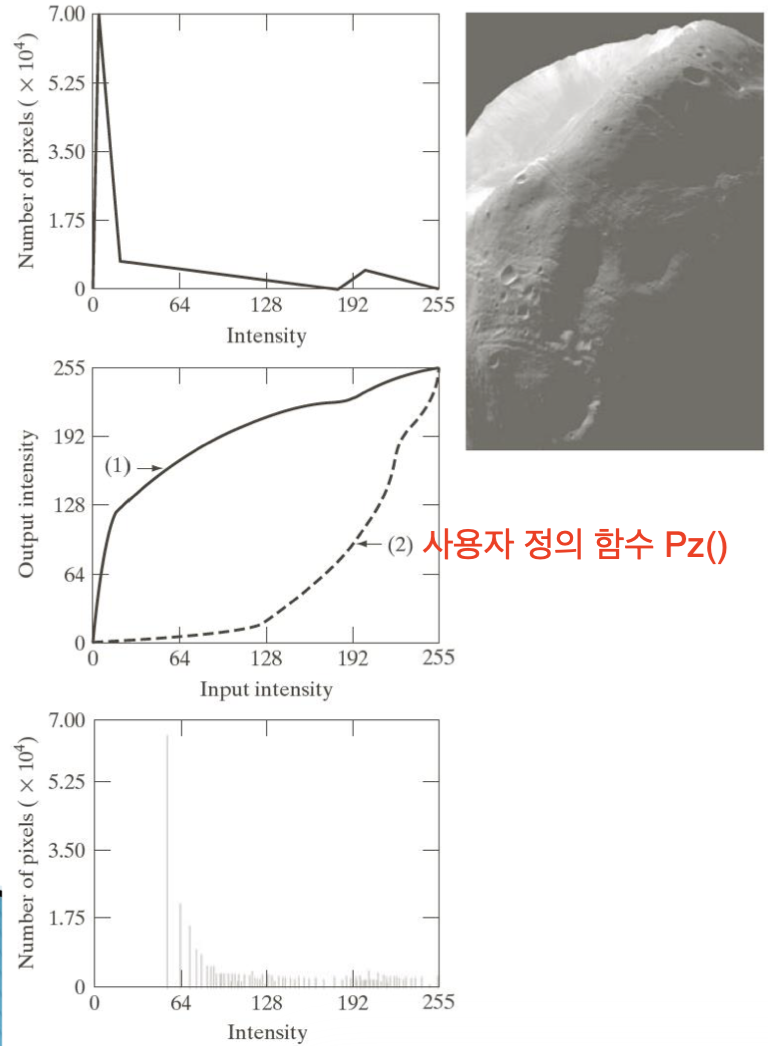
하지만 히스토그램을 이용한 Equalization이 만능인 것은 아니다.
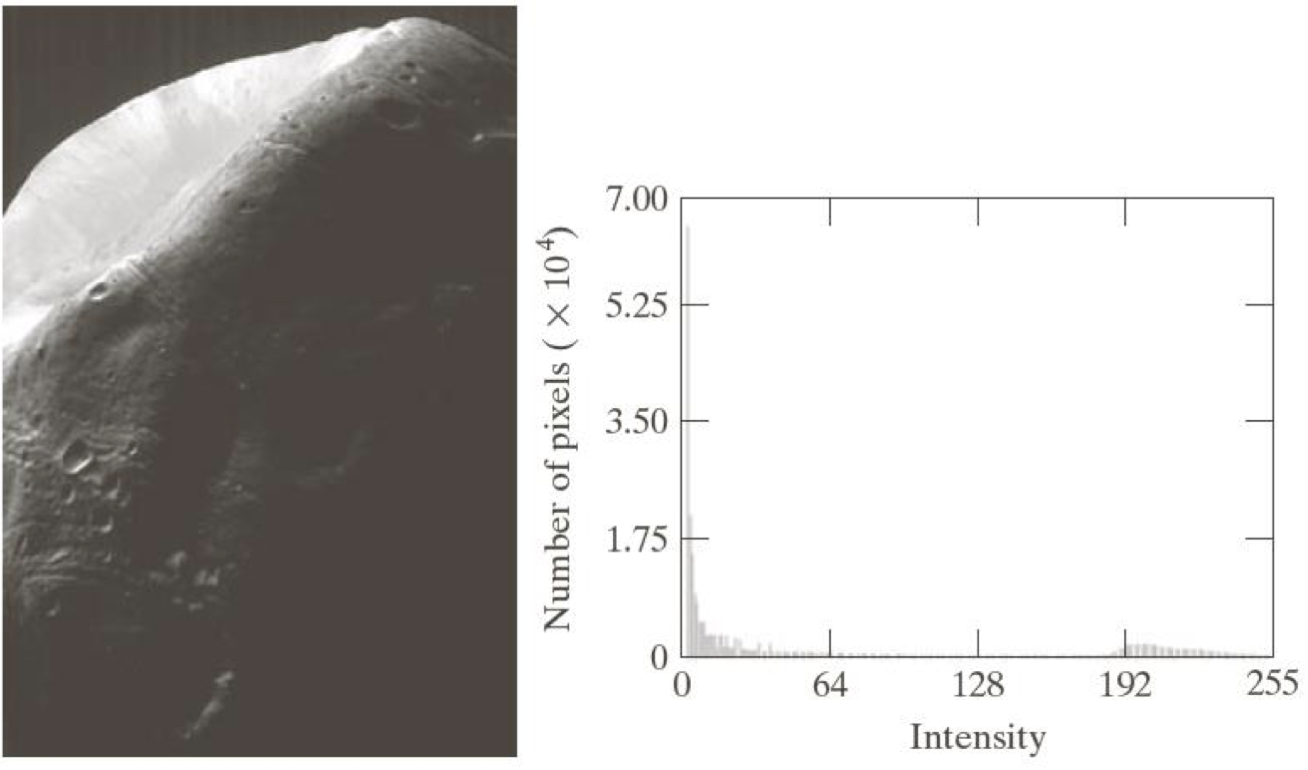
이런 영상처럼 너무 극단으로 몰린 경우에 적용한 결과는 다음과 같이 나올 수 있는데,
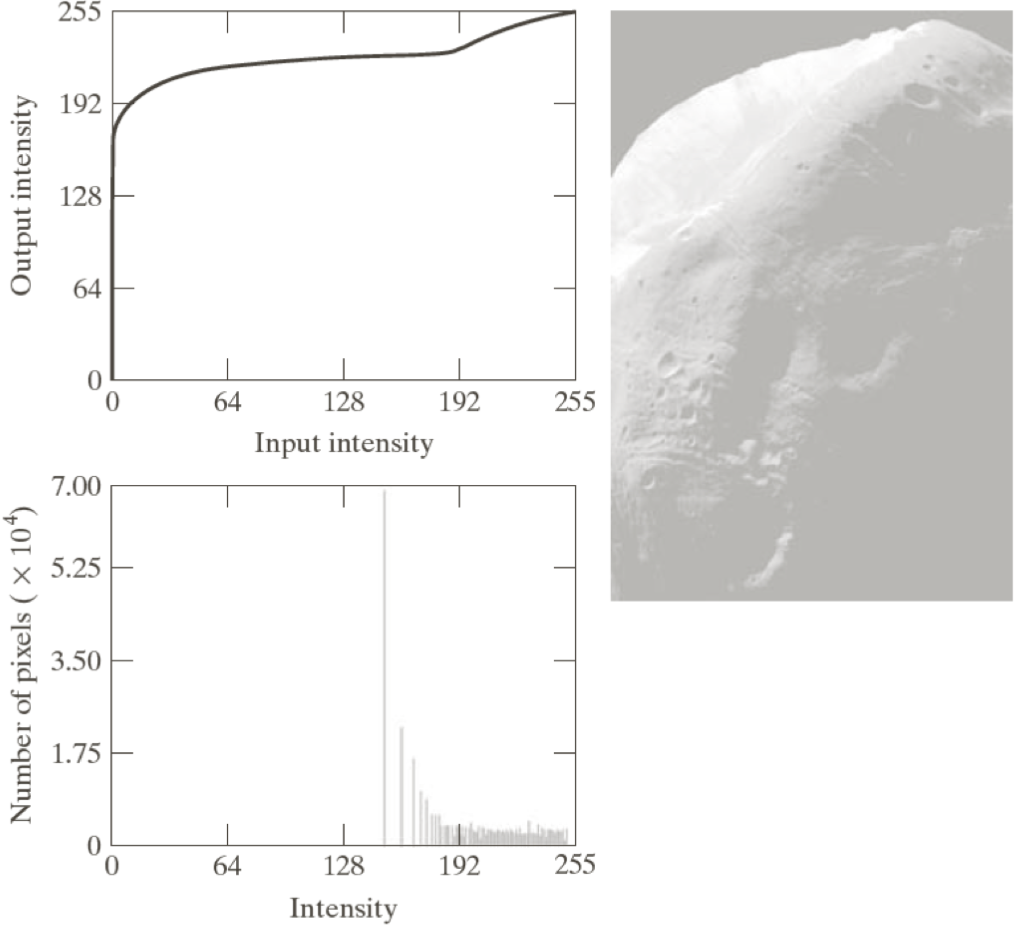
이런 경우에는 단순히 를 사용하여 변환 함수를 구하는 것 보다,
사용자 정의 함수 를 만들어서 처리하는게 더 좋은 영상을 만들 수 있다.